Mutual information

Definition

Formally, the mutual information of two discrete random variables X and Y can be defined as:

where p(x,y) is the joint probability distribution function of X and Y, and p ( x ) and p ( y ) are the marginal probability distribution functions of X and Y respectively.

In the case of continuous random variables, the summation is replaced by a definite double integral:

where p(x,y) is now the joint probability density function of X and Y, and p ( x ) and p ( y ) are the marginal probability density functions of X and Y respectively.

If the log base 2 is used, the units of mutual information are the bit.

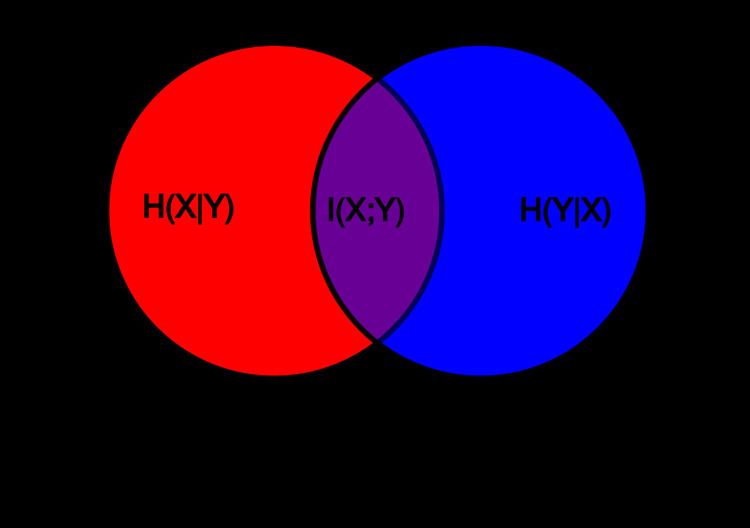
Intuitively, mutual information measures the information that X and Y share: it measures how much knowing one of these variables reduces uncertainty about the other. For example, if X and Y are independent, then knowing X does not give any information about Y and vice versa, so their mutual information is zero. At the other extreme, if X is a deterministic function of Y and Y is a deterministic function of X then all information conveyed by X is shared with Y: knowing X determines the value of Y and vice versa. As a result, in this case the mutual information is the same as the uncertainty contained in Y (or X) alone, namely the entropy of Y (or X). Moreover, this mutual information is the same as the entropy of X and as the entropy of Y. (A very special case of this is when X and Y are the same random variable.)

Mutual information is a measure of the inherent dependence expressed in the joint distribution of X and Y relative to the joint distribution of X and Y under the assumption of independence. Mutual information therefore measures dependence in the following sense: I(X; Y) = 0 if and only if X and Y are independent random variables. This is easy to see in one direction: if X and Y are independent, then p(x,y) = p(x) p(y), and therefore:

Moreover, mutual information is nonnegative (i.e. I(X;Y) ≥ 0; see below) and symmetric (i.e. I(X;Y) = I(Y;X)).

Relation to other quantities

Mutual information can be equivalently expressed as

where   H ( X ) and   H ( Y ) are the marginal entropies, H(X|Y) and H(Y|X) are the conditional entropies, and H(X,Y) is the joint entropy of X and Y. Note the analogy to the union, difference, and intersection of two sets, as illustrated in the Venn diagram.

Using Jensen's inequality on the definition of mutual information we can show that I(X;Y) is non-negative, consequently,   H ( X ) ≥ H ( X | Y ) . Here we give the detailed deduction of I(X;Y) = H(Y) – H(Y|X):

The proofs of the other identities above are similar.

Intuitively, if entropy H(Y) is regarded as a measure of uncertainty about a random variable, then H(Y|X) is a measure of what X does not say about Y. This is "the amount of uncertainty remaining about Y after X is known", and thus the right side of the first of these equalities can be read as "the amount of uncertainty in Y, minus the amount of uncertainty in Y which remains after X is known", which is equivalent to "the amount of uncertainty in Y which is removed by knowing X". This corroborates the intuitive meaning of mutual information as the amount of information (that is, reduction in uncertainty) that knowing either variable provides about the other.

Note that in the discrete case H(X|X) = 0 and therefore H(X) = I(X;X). Thus I(X;X) ≥ I(X;Y), and one can formulate the basic principle that a variable contains at least as much information about itself as any other variable can provide.

Mutual information can also be expressed as a Kullback–Leibler divergence of the product p(x) × p(y) of the marginal distributions of the two random variables X and Y, from p(x,y) the random variables' joint distribution:

Furthermore, let p(x|y) = p(x, y) / p(y). Then

Note that here the Kullback-Leibler divergence involves integration with respect to the random variable X only and the expression D K L ( p ( x | y ) ∥ p ( x ) ) is now a random variable in Y. Thus mutual information can also be understood as the expectation of the Kullback–Leibler divergence of the univariate distribution p(x) of X from the conditional distribution p(x|y) of X given Y: the more different the distributions p(x|y) and p(x) are on average, the greater the information gain.

Variations

Several variations on mutual information have been proposed to suit various needs. Among these are normalized variants and generalizations to more than two variables.

Metric

Many applications require a metric, that is, a distance measure between pairs of points. The quantity

satisfies the properties of a metric (triangle inequality, non-negativity, indiscernability and symmetry). This distance metric is also known as the Variation of information.

If X , Y are discrete random variables then all the entropy terms are non-negative, so 0 ≤ d ( X , Y ) ≤ H ( X , Y ) and one can define a normalized distance

The metric D is a universal metric, in that if any other distance measure places X and Y close-by, then the D will also judge them close.

Plugging in the definitions shows that

In a set-theoretic interpretation of information (see the figure for Conditional entropy), this is effectively the Jaccard distance between X and Y.

Finally,

is also a metric.

Conditional mutual information

Sometimes it is useful to express the mutual information of two random variables conditioned on a third.

which can be simplified as

Conditioning on a third random variable may either increase or decrease the mutual information, but it is always true that

for discrete, jointly distributed random variables X, Y, Z. This result has been used as a basic building block for proving other inequalities in information theory.

Multivariate mutual information

Several generalizations of mutual information to more than two random variables have been proposed, such as total correlation and interaction information. If Shannon entropy is viewed as a signed measure in the context of information diagrams, as explained in the article Information theory and measure theory, then the only definition of multivariate mutual information that makes sense is as follows:

and for n > 1 ,

where (as above) we define

(This definition of multivariate mutual information is identical to that of interaction information except for a change in sign when the number of random variables is odd.)

Applications

Applying information diagrams blindly to derive the above definition has been criticised, and indeed it has found rather limited practical application since it is difficult to visualize or grasp the significance of this quantity for a large number of random variables. It can be zero, positive, or negative for any odd number of variables n ≥ 3.

One high-dimensional generalization scheme which maximizes the mutual information between the joint distribution and other target variables is found to be useful in feature selection.

Mutual information is also used in the area of signal processing as a measure of similarity between two signals. For example, FMI metric is an image fusion performance measure that makes use of mutual information in order to measure the amount of information that the fused image contains about the source images. The Matlab code for this metric can be found at.

Directed information

Directed information, I ( X n → Y n ) , measures the amount of information that flows from the process X n to Y n , where X n denotes the vector X 1 , X 2 , . . . , X n and Y n denotes Y 1 , Y 2 , . . . , Y n . The term "directed information" was coined by James Massey and is defined as

Note that if n = 1 the directed information becomes the mutual information. Directed information has many applications in problems where causality plays an important role, such as capacity of channel with feedback.

Normalized variants

Normalized variants of the mutual information are provided by the coefficients of constraint, uncertainty coefficient or proficiency:

The two coefficients are not necessarily equal. In some cases a symmetric measure may be desired, such as the following redundancy measure:

which attains a minimum of zero when the variables are independent and a maximum value of

when one variable becomes completely redundant with the knowledge of the other. See also Redundancy (information theory). Another symmetrical measure is the symmetric uncertainty (Witten & Frank 2005), given by

which represents the harmonic mean of the two uncertainty coefficients C X Y , C Y X .

If we consider mutual information as a special case of the total correlation or dual total correlation, the normalized version are respectively,

This normalized version also known as Information Quality Ratio (IQR) which quantifies the amount of information of a variable based on another variable against total uncertainty:

There's a normalization which derives from first thinking of mutual information as an analogue to covariance (thus Shannon entropy is analogous to variance). Then the normalized mutual information is calculated akin to the Pearson correlation coefficient,

Weighted variants

In the traditional formulation of the mutual information,

each event or object specified by ( x , y ) is weighted by the corresponding probability p ( x , y ) . This assumes that all objects or events are equivalent apart from their probability of occurrence. However, in some applications it may be the case that certain objects or events are more significant than others, or that certain patterns of association are more semantically important than others.

For example, the deterministic mapping { ( 1 , 1 ) , ( 2 , 2 ) , ( 3 , 3 ) } may be viewed as stronger than the deterministic mapping { ( 1 , 3 ) , ( 2 , 1 ) , ( 3 , 2 ) } , although these relationships would yield the same mutual information. This is because the mutual information is not sensitive at all to any inherent ordering in the variable values (Cronbach 1954, Coombs, Dawes & Tversky 1970, Lockhead 1970), and is therefore not sensitive at all to the form of the relational mapping between the associated variables. If it is desired that the former relation—showing agreement on all variable values—be judged stronger than the later relation, then it is possible to use the following weighted mutual information (Guiasu 1977).

which places a weight w ( x , y ) on the probability of each variable value co-occurrence, p ( x , y ) . This allows that certain probabilities may carry more or less significance than others, thereby allowing the quantification of relevant holistic or prägnanz factors. In the above example, using larger relative weights for w ( 1 , 1 ) , w ( 2 , 2 ) , and w ( 3 , 3 ) would have the effect of assessing greater informativeness for the relation { ( 1 , 1 ) , ( 2 , 2 ) , ( 3 , 3 ) } than for the relation { ( 1 , 3 ) , ( 2 , 1 ) , ( 3 , 2 ) } , which may be desirable in some cases of pattern recognition, and the like. This weighted mutual information is a form of weighted KL-Divergence, which is known to take negative values for some inputs, and there are examples where the weighted mutual information also takes negative values.

Adjusted mutual information

A probability distribution can be viewed as a partition of a set. One may then ask: if a set were partitioned randomly, what would the distribution of probabilities be? What would the expectation value of the mutual information be? The adjusted mutual information or AMI subtracts the expectation value of the MI, so that the AMI is zero when two different distributions are random, and one when two distributions are identical. The AMI is defined in analogy to the adjusted Rand index of two different partitions of a set.

Absolute mutual information

Using the ideas of Kolmogorov complexity, one can consider the mutual information of two sequences independent of any probability distribution:

To establish that this quantity is symmetric up to a logarithmic factor ( I K ( X ; Y ) ≈ I K ( Y ; X ) ) requires the chain rule for Kolmogorov complexity (Li & Vitányi 1997). Approximations of this quantity via compression can be used to define a distance measure to perform a hierarchical clustering of sequences without having any domain knowledge of the sequences (Cilibrasi & Vitányi 2005).

Linear correlation

Unlike correlation coefficients, such as the product moment correlation coefficient, mutual information contains information about all dependence—linear and nonlinear—and not just linear dependence as the correlation coefficient measures. However, in the narrow case that both marginal distributions for X and Y are normally distributed and their joint distribution is a bivariate normal distribution, there is an exact relationship between I and the correlation coefficient ρ (Gel'fand & Yaglom 1957).

For discrete data

When X and Y are limited to be in a discrete number of states, observation data is summarized in a contingency table, with row variable X (or i) and column variable Y (or j). Mutual information is one of the measures of association or correlation between the row and column variables. Other measures of association include Pearson's chi-squared test statistics, G-test statistics, etc. In fact, mutual information is equal to G-test statistics divided by 2N where N is the sample size.

In the special case where the number of states for both row and column variables is 2 (i,j=1,2), the degrees of freedom of the Pearson's chi-squared test is 1. Out of the four terms in the summation:

only one is independent. It is the reason that mutual information function has an exact relationship with the correlation function p X = 1 , Y = 1 − p X = 1 p Y = 1 for binary sequences .

Applications

In many applications, one wants to maximize mutual information (thus increasing dependencies), which is often equivalent to minimizing conditional entropy. Examples include: