Hierarchical clustering

Cluster dissimilarity

In order to decide which clusters should be combined (for agglomerative), or where a cluster should be split (for divisive), a measure of dissimilarity between sets of observations is required. In most methods of hierarchical clustering, this is achieved by use of an appropriate metric (a measure of distance between pairs of observations), and a linkage criterion which specifies the dissimilarity of sets as a function of the pairwise distances of observations in the sets.

Metric

The choice of an appropriate metric will influence the shape of the clusters, as some elements may be close to one another according to one distance and farther away according to another. For example, in a 2-dimensional space, the distance between the point (1,0) and the origin (0,0) is always 1 according to the usual norms, but the distance between the point (1,1) and the origin (0,0) can be 2 under Manhattan distance, 2 under Euclidean distance, or 1 under maximum distance.

Some commonly used metrics for hierarchical clustering are:

For text or other non-numeric data, metrics such as the Hamming distance or Levenshtein distance are often used.

A review of cluster analysis in health psychology research found that the most common distance measure in published studies in that research area is the Euclidean distance or the squared Euclidean distance.

Linkage criteria

The linkage criterion determines the distance between sets of observations as a function of the pairwise distances between observations.

Some commonly used linkage criteria between two sets of observations A and B are:

where d is the chosen metric. Other linkage criteria include:

Discussion

Hierarchical clustering has the distinct advantage that any valid measure of distance can be used. In fact, the observations themselves are not required: all that is used is a matrix of distances.

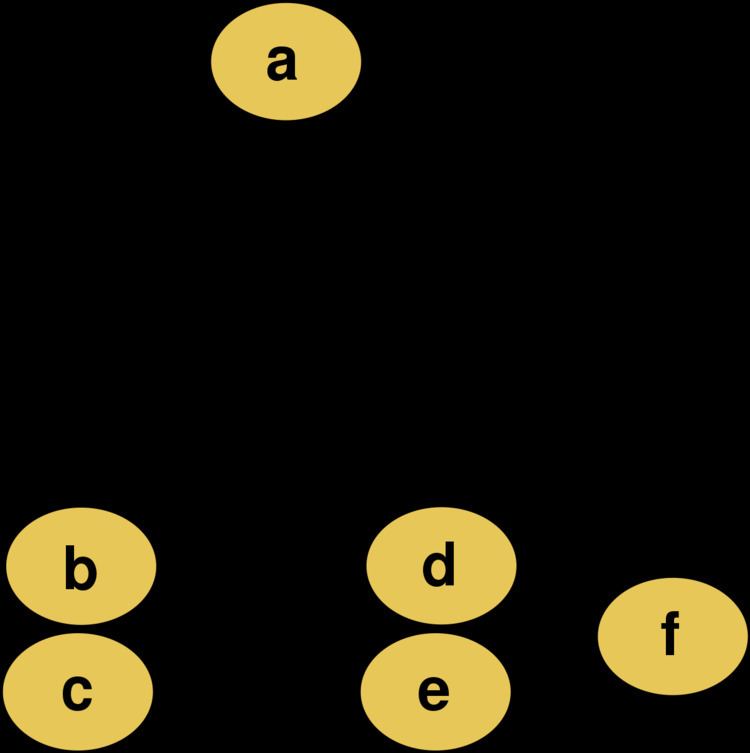
Agglomerative clustering example

For example, suppose this data is to be clustered, and the Euclidean distance is the distance metric.

Cutting the tree at a given height will give a partitioning clustering at a selected precision. In this example, cutting after the second row of the dendrogram will yield clusters {a} {b c} {d e} {f}. Cutting after the third row will yield clusters {a} {b c} {d e f}, which is a coarser clustering, with a smaller number but larger clusters.

The hierarchical clustering dendrogram would be as such:

This method builds the hierarchy from the individual elements by progressively merging clusters. In our example, we have six elements {a} {b} {c} {d} {e} and {f}. The first step is to determine which elements to merge in a cluster. Usually, we want to take the two closest elements, according to the chosen distance.

Optionally, one can also construct a distance matrix at this stage, where the number in the i-th row j-th column is the distance between the i-th and j-th elements. Then, as clustering progresses, rows and columns are merged as the clusters are merged and the distances updated. This is a common way to implement this type of clustering, and has the benefit of caching distances between clusters. A simple agglomerative clustering algorithm is described in the single-linkage clustering page; it can easily be adapted to different types of linkage (see below).

Suppose we have merged the two closest elements b and c, we now have the following clusters {a}, {b, c}, {d}, {e} and {f}, and want to merge them further. To do that, we need to take the distance between {a} and {b c}, and therefore define the distance between two clusters. Usually the distance between two clusters A and B is one of the following:

Each agglomeration occurs at a greater distance between clusters than the previous agglomeration, and one can decide to stop clustering either when the clusters are too far apart to be merged (distance criterion) or when there is a sufficiently small number of clusters (number criterion).

Divisive clustering

The basic principle of divisive clustering was published as the DIANA (DIvisive ANAlysis Clustering) algorithm. Initially, all data is in the same cluster, and the largest cluster is split until every object is separate. Because there exist O ( 2 n ) ways of splitting each cluster, heuristics are needed. DIANA chooses the object with the maximum average dissimilarity and then moves all objects to this cluster that are more similar to the new cluster than to the remainder. An obvious alternate choice is k-means clustering with k = 2 , but any other clustering algorithm can be used that always produces at least two clusters.

Open source implementations

Commercial