In information theory, the conditional entropy (or equivocation) quantifies the amount of information needed to describe the outcome of a random variable Y given that the value of another random variable X is known. Here, information is measured in shannons, nats, or hartleys. The entropy of Y conditioned on X is written as H ( Y | X ) .
If H ( Y | X = x ) is the entropy of the variable Y conditioned on the variable X taking a certain value x , then H ( Y | X ) is the result of averaging H ( Y | X = x ) over all possible values x that X may take.
Given discrete random variables X with Image X and Y with Image Y , the conditional entropy of Y given X is defined as: (Intuitively, the following can be thought as the weighted sum of H ( Y | X = x ) for each possible value of x , using p ( x ) as the weights)
H ( Y | X ) ≡ ∑ x ∈ X p ( x ) H ( Y | X = x ) = − ∑ x ∈ X p ( x ) ∑ y ∈ Y p ( y | x ) log p ( y | x ) = − ∑ x ∈ X ∑ y ∈ Y p ( x , y ) log p ( y | x ) = − ∑ x ∈ X , y ∈ Y p ( x , y ) log p ( y | x ) = − ∑ x ∈ X , y ∈ Y p ( x , y ) log p ( x , y ) p ( x ) . = ∑ x ∈ X , y ∈ Y p ( x , y ) log p ( x ) p ( x , y ) .
Note: It is understood that the expressions 0 log 0 and 0 log (c/0) for fixed c>0 should be treated as being equal to zero.
H ( Y | X ) = 0 if and only if the value of Y is completely determined by the value of X . Conversely, H ( Y | X ) = H ( Y ) if and only if Y and X are independent random variables.
Assume that the combined system determined by two random variables X and Y has joint entropy H ( X , Y ) , that is, we need H ( X , Y ) bits of information to describe its exact state. Now if we first learn the value of X , we have gained H ( X ) bits of information. Once X is known, we only need H ( X , Y ) − H ( X ) bits to describe the state of the whole system. This quantity is exactly H ( Y | X ) , which gives the chain rule of conditional entropy:
H ( Y | X ) = H ( X , Y ) − H ( X ) . The chain rule follows from the above definition of conditional entropy:
H ( Y | X ) = ∑ x ∈ X , y ∈ Y p ( x , y ) log ( p ( x ) p ( x , y ) ) = − ∑ x ∈ X , y ∈ Y p ( x , y ) log ( p ( x , y ) ) + ∑ x ∈ X , y ∈ Y p ( x , y ) log ( p ( x ) ) = H ( X , Y ) + ∑ x ∈ X p ( x ) log ( p ( x ) ) = H ( X , Y ) − H ( X ) . In general, a chain rule for multiple random variables holds:
H ( X 1 , X 2 , … , X n ) = ∑ i = 1 n H ( X i | X 1 , … , X i − 1 ) It has a similar form to Chain rule (probability) in probability theory, except that addition instead of multiplication is used.
Bayes' rule for conditional entropy states
H ( Y | X ) = H ( X | Y ) − H ( X ) + H ( Y ) . Proof. H ( Y | X ) = H ( X , Y ) − H ( X ) and H ( X | Y ) = H ( Y , X ) − H ( Y ) . Symmetry implies H ( X , Y ) = H ( Y , X ) . Subtracting the two equations implies Bayes' rule.
If Y is conditional independent of Z given X we have:
H ( Y | X , Z ) = H ( Y | X ) . In quantum information theory, the conditional entropy is generalized to the conditional quantum entropy. The latter can take negative values, unlike its classical counterpart. Bayes' rule does not hold for conditional quantum entropy, since H ( X , Y ) ≠ H ( Y , X ) .
For any X and Y :
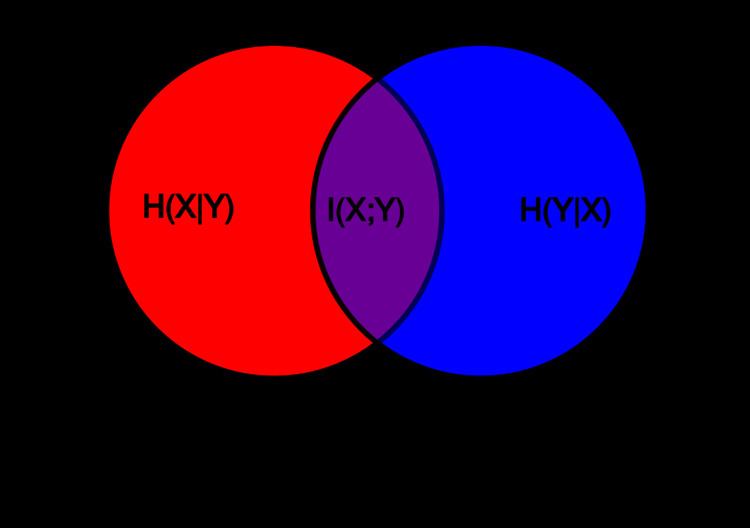
H ( Y | X ) ≤ H ( Y ) H ( X , Y ) = H ( X | Y ) + H ( Y | X ) + I ( X ; Y ) , H ( X , Y ) = H ( X ) + H ( Y ) − I ( X ; Y ) , I ( X ; Y ) ≤ H ( X ) , where I ( X ; Y ) is the mutual information between X and Y .
For independent X and Y :
H ( Y | X ) = H ( Y ) and H ( X | Y ) = H ( X ) Although the specific-conditional entropy, H ( X | Y = y ) , can be either less or greater than H ( X ) , H ( X | Y ) can never exceed H ( X ) .