Extreme value theory

Data analysis

Two approaches exist for practical extreme value analysis.

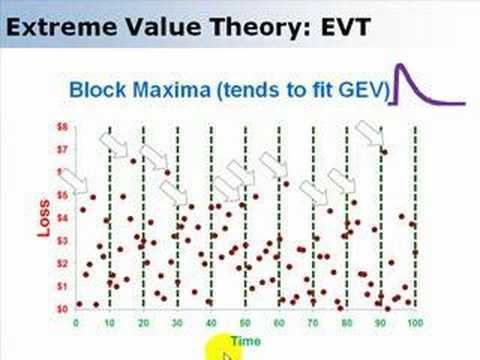
The first method relies on deriving block maxima (minima) series as a preliminary step. In many situations it is customary and convenient to extract the annual maxima (minima), generating an "Annual Maxima Series" (AMS).

The second method relies on extracting, from a continuous record, the peak values reached for any period during which values exceed a certain threshold (falls below a certain threshold). This method is generally referred to as the "Peak Over Threshold" method (POT).

For AMS data, the analysis may partly rely on the results of the Fisher–Tippett–Gnedenko theorem, leading to the generalized extreme value distribution being selected for fitting. However, in practice, various procedures are applied to select between a wider range of distributions. The theorem here relates to the limiting distributions for the minimum or the maximum of a very large collection of independent random variables from the same distribution. Given that the number of relevant random events within a year may be rather limited, it is unsurprising that analyses of observed AMS data often lead to distributions other than the generalized extreme value distribution (GEVD) being selected.

For POT data, the analysis may involve fitting two distributions: one for the number of events in a time period considered and a second for the size of the exceedances.

A common assumption for the first is the Poisson distribution, with the generalized Pareto distribution being used for the exceedances. A tail-fitting can be based on the Pickands–Balkema–de Haan theorem.

Novak reserves the term “POT method” to the case where the threshold is non-random, and distinguishes it from the case where one deals with exceedances of a random threshold.

Applications

Applications of extreme value theory include predicting the probability distribution of:

History

The field of extreme value theory was pioneered by Leonard Tippett (1902–1985). Tippett was employed by the British Cotton Industry Research Association, where he worked to make cotton thread stronger. In his studies, he realized that the strength of a thread was controlled by the strength of its weakest fibres. With the help of R. A. Fisher, Tippet obtained three asymptotic limits describing the distributions of extremes. Emil Julius Gumbel codified this theory in his 1958 book Statistics of Extremes, including the Gumbel distributions that bear his name.

A summary of historically important publications relating to extreme value theory can be found on the article List of publications in statistics.

Univariate theory

Let X 1 , … , X n be a sequence of independent and identically distributed variables with cumulative distribution function F and let M n = max ( X 1 , … , X n ) denote the maximum.

In theory, the exact distribution of the maximum can be derived:

The associated indicator function I n = I ( M n > z ) is a Bernoulli process with a success probability p ( z ) = ( 1 − ( F ( z ) ) n ) that depends on the magnitude z of the extreme event. The number of extreme events within n trials thus follows a binomial distribution and the number of trials until an event occurs follows a geometric distribution with expected value and standard deviation of the same order O ( 1 / p ( z ) ) .

In practice, we might not have the distribution function F but the Fisher–Tippett–Gnedenko theorem provides an asymptotic result. If there exist sequences of constants a n > 0 and b n ∈ R such that

as n → ∞ then

where ζ depends on the tail shape of the distribution. When normalized, G belongs to one of the following non-degenerate distribution families:

Weibull law: G ( z ) = { exp ⁡ { − ( − ( z − b a ) ) α } z < b 1 z ≥ b when the distribution of M n has a light tail with finite upper bound. Also known as Type 3.

Gumbel law: G ( z ) = exp ⁡ { − exp ⁡ ( − ( z − b a ) ) }  for  z ∈ R . when the distribution of M n has an exponential tail. Also known as Type 1

Fréchet Law: G ( z ) = { 0 z ≤ b exp ⁡ { − ( z − b a ) − α } z > b . when the distribution of M n has a heavy tail (including polynomial decay). Also known as Type 2.

In all cases, α > 0 .