Notation B(n, p) | ||
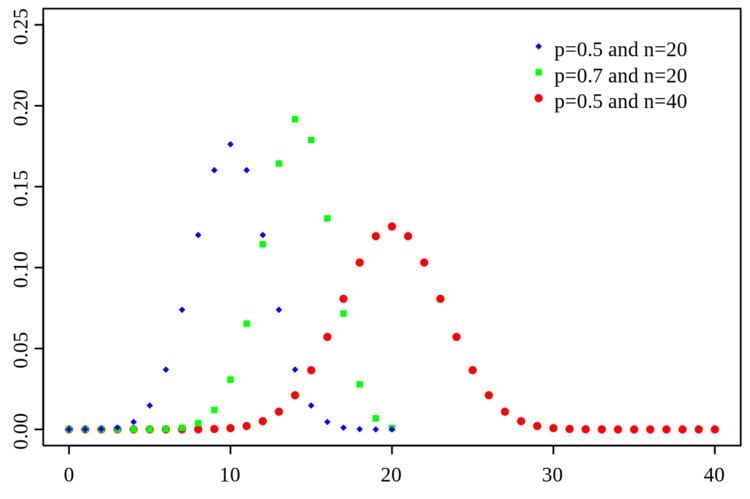 | ||
Parameters n ∈ N0 — number of trialsp ∈ [0,1] — success probability in each trial Support k ∈ { 0, …, n } — number of successes pmf ( n k ) p k ( 1 − p ) n − k {displaystyle extstyle {n choose k},p^{k}(1-p)^{n-k}} CDF I 1 − p ( n − k , 1 + k ) {displaystyle extstyle I_{1-p}(n-k,1+k)} Mean n p {displaystyle np} | ||
In probability theory and statistics, the binomial distribution with parameters n and p is the discrete probability distribution of the number of successes in a sequence of n independent yes/no experiments, each of which yields success with probability p. A success/failure experiment is also called a Bernoulli experiment or Bernoulli trial; when n = 1, the binomial distribution is a Bernoulli distribution. The binomial distribution is the basis for the popular binomial test of statistical significance.
Contents
- Probability mass function
- Cumulative distribution function
- Example
- Mean
- Variance
- Mode
- Median
- Covariance between two binomials
- Sums of binomials
- Conditional binomials
- Bernoulli distribution
- Poisson binomial distribution
- Normal approximation
- Poisson approximation
- Limiting distributions
- Beta distribution
- Confidence intervals
- Generating binomial random variates
- Tail bounds
- References
The binomial distribution is frequently used to model the number of successes in a sample of size n drawn with replacement from a population of size N. If the sampling is carried out without replacement, the draws are not independent and so the resulting distribution is a hypergeometric distribution, not a binomial one. However, for N much larger than n, the binomial distribution remains a good approximation, and is widely used.
Probability mass function
In general, if the random variable X follows the binomial distribution with parameters n ∈ ℕ and p ∈ [0,1], we write X ~ B(n, p). The probability of getting exactly k successes in n trials is given by the probability mass function:
for k = 0, 1, 2, ..., n, where
is the binomial coefficient, hence the name of the distribution. The formula can be understood as follows. k successes occur with probability pk and n − k failures occur with probability (1 − p)n − k. However, the k successes can occur anywhere among the n trials, and there are
In creating reference tables for binomial distribution probability, usually the table is filled in up to n/2 values. This is because for k > n/2, the probability can be calculated by its complement as
The probability mass function satisfies the following recurrence relation, for every
Looking at the expression ƒ(k, n, p) as a function of k, there is a k value that maximizes it. This k value can be found by calculating
and comparing it to 1. There is always an integer M that satisfies
ƒ(k, n, p) is monotone increasing for k < M and monotone decreasing for k > M, with the exception of the case where (n + 1)p is an integer. In this case, there are two values for which ƒ is maximal: (n + 1)p and (n + 1)p − 1. M is the most probable (most likely) outcome of the Bernoulli trials and is called the mode. Note that the probability of it occurring can be fairly small.
Cumulative distribution function
The cumulative distribution function can be expressed as:
where
It can also be represented in terms of the regularized incomplete beta function, as follows:
Some closed-form bounds for the cumulative distribution function are given below.
Example
Suppose a biased coin comes up heads with probability 0.3 when tossed. What is the probability of achieving 0, 1,..., 6 heads after six tosses?
Mean
If X ~ B(n, p), that is, X is a binomially distributed random variable, n being the total number of experiments and p the probability of each experiment yielding a successful result, then the expected value of X is:
For example, if n = 100, and p =1/4, then the average number of successful results will be 25.
Proof: We calculate the mean, μ, directly calculated from its definition
and the binomial theorem:
It is also possible to deduce the mean from the equation
Variance
The variance is:
Proof: Let
Mode
Usually the mode of a binomial B(n, p) distribution is equal to
Proof: Let
For
Let
From this follows
So when
Median
In general, there is no single formula to find the median for a binomial distribution, and it may even be non-unique. However several special results have been established:
Covariance between two binomials
If two binomially distributed random variables X and Y are observed together, estimating their covariance can be useful. Using the definition of covariance, in the case n = 1 (thus being Bernoulli trials) we have
The first term is non-zero only when both X and Y are one, and μX and μY are equal to the two probabilities. Defining pB as the probability of both happening at the same time, this gives
and for n independent pairwise trials
If X and Y are the same variable, this reduces to the variance formula given above.
Sums of binomials
If X ~ B(n, p) and Y ~ B(m, p) are independent binomial variables with the same probability p, then X + Y is again a binomial variable; its distribution is Z=X+Y ~ B(n+m, p):
However, if X and Y do not have the same probability p, then the variance of the sum will be smaller than the variance of a binomial variable distributed as
Conditional binomials
If X ~ B(n, p) and, conditional on X, Y ~ B(X, q), then Y is a simple binomial variable with distribution
For example, imagine throwing n balls to a basket UX and taking the balls that hit and throwing them to another basket UY. If p is the probability to hit UX then X ~ B(n, p) is the number of balls that hit UX. If q is the probability to hit UY then the number of balls that hit UY is Y ~ B(X, q) and therefore Y ~ B(n, pq).
Bernoulli distribution
The Bernoulli distribution is a special case of the binomial distribution, where n = 1. Symbolically, X ~ B(1, p) has the same meaning as X ~ B(p). Conversely, any binomial distribution, B(n, p), is the distribution of the sum of n Bernoulli trials, B(p), each with the same probability p.
Poisson binomial distribution
The binomial distribution is a special case of the Poisson binomial distribution, or general binomial distribution, which is the distribution of a sum of n independent non-identical Bernoulli trials B(pi).
Normal approximation
If n is large enough, then the skew of the distribution is not too great. In this case a reasonable approximation to B(n, p) is given by the normal distribution
and this basic approximation can be improved in a simple way by using a suitable continuity correction. The basic approximation generally improves as n increases (at least 20) and is better when p is not near to 0 or 1. Various rules of thumb may be used to decide whether n is large enough, and p is far enough from the extremes of zero or one:
The following is an example of applying a continuity correction. Suppose one wishes to calculate Pr(X ≤ 8) for a binomial random variable X. If Y has a distribution given by the normal approximation, then Pr(X ≤ 8) is approximated by Pr(Y ≤ 8.5). The addition of 0.5 is the continuity correction; the uncorrected normal approximation gives considerably less accurate results.
This approximation, known as de Moivre–Laplace theorem, is a huge time-saver when undertaking calculations by hand (exact calculations with large n are very onerous); historically, it was the first use of the normal distribution, introduced in Abraham de Moivre's book The Doctrine of Chances in 1738. Nowadays, it can be seen as a consequence of the central limit theorem since B(n, p) is a sum of n independent, identically distributed Bernoulli variables with parameter p. This fact is the basis of a hypothesis test, a "proportion z-test", for the value of p using x/n, the sample proportion and estimator of p, in a common test statistic.
For example, suppose one randomly samples n people out of a large population and ask them whether they agree with a certain statement. The proportion of people who agree will of course depend on the sample. If groups of n people were sampled repeatedly and truly randomly, the proportions would follow an approximate normal distribution with mean equal to the true proportion p of agreement in the population and with standard deviation
Poisson approximation
The binomial distribution converges towards the Poisson distribution as the number of trials goes to infinity while the product np remains fixed or at least p tends to zero. Therefore, the Poisson distribution with parameter λ = np can be used as an approximation to B(n, p) of the binomial distribution if n is sufficiently large and p is sufficiently small. According to two rules of thumb, this approximation is good if n ≥ 20 and p ≤ 0.05, or if n ≥ 100 and np ≤ 10.
Concerning the accuracy of Poisson approximation, see Novak, ch. 4, and references therein.
Limiting distributions
Beta distribution
Beta distributions provide a family of prior probability distributions for binomial distributions in Bayesian inference:
Confidence intervals
Even for quite large values of n, the actual distribution of the mean is significantly nonnormal. Because of this problem several methods to estimate confidence intervals have been proposed.
Let n1 be the number of successes out of n, the total number of trials, and let
be the proportion of successes. Let zα/2 be the 100(1 − α/2)th percentile of the standard normal distribution.
The exact (Clopper-Pearson) method is the most conservative. The Wald method although commonly recommended in the text books is the most biased.
Generating binomial random variates
Methods for random number generation where the marginal distribution is a binomial distribution are well-established.
One way to generate random samples from a binomial distribution is to use an inversion algorithm. To do so, one must calculate the probability that P(X=k) for all values k from 0 through n. (These probabilities should sum to a value close to one, in order to encompass the entire sample space.) Then by using a pseudorandom number generator to generate samples uniformly between 0 and 1, one can transform the calculated samples U[0,1] into discrete numbers by using the probabilities calculated in step one.
Tail bounds
For k ≤ np, upper bounds for the lower tail of the distribution function can be derived. Recall that
Hoeffding's inequality yields the bound
and Chernoff's inequality can be used to derive the bound
Moreover, these bounds are reasonably tight when p = 1/2, since the following expression holds for all k ≥ 3n/8
However, the bounds do not work well for extreme values of p. In particular, as p
where D(a|| p) is the relative entropy between an a-coin and a p-coin (i.e. between the Bernoulli(a) and Bernoulli(p) distribution):
Asymptotically, this bound is reasonably tight; see for details. An equivalent formulation of the bound is
Both these bounds are derived directly from the Chernoff bound. It can also be shown that,
This is proved using the method of types (see for example chapter 12 of Elements of Information Theory by Cover and Thomas ).
We can also change the
