 | ||
In mathematics, a Gaussian function, often simply referred to as a Gaussian, is a function of the form:
Contents
- Properties
- Integral of a Gaussian function
- Proof
- Two dimensional Gaussian function
- Meaning of parameters for the general equation
- Higher order Gaussian or Super Gaussian function
- Multi dimensional Gaussian function
- Gaussian profile estimation
- Discrete Gaussian
- Applications
- References
for arbitrary real constants a, b and c. It is named after the mathematician Carl Friedrich Gauss.
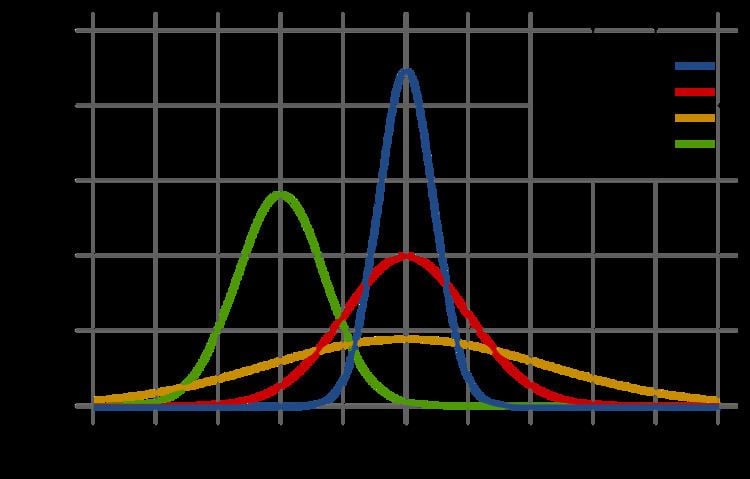
The graph of a Gaussian is a characteristic symmetric "bell curve" shape. The parameter a is the height of the curve's peak, b is the position of the center of the peak and c (the standard deviation, sometimes called the Gaussian RMS width) controls the width of the "bell".
Gaussian functions are widely used in statistics to describe the normal distributions, in signal processing to define Gaussian filters, in image processing where two-dimensional Gaussians are used for Gaussian blurs, and in mathematics to solve heat equations and diffusion equations and to define the Weierstrass transform.
Properties
Gaussian functions arise by composing the exponential function with a concave quadratic function. The Gaussian functions are thus those functions whose logarithm is a concave quadratic function.
The parameter c is related to the full width at half maximum (FWHM) of the peak according to
The function may then be expressed in terms of the FWHM, represented by w:
Alternatively, the parameter c can be interpreted by saying that the two inflection points of the function occur at x = b − c and x = b + c.
The full width at tenth of maximum (FWTM) for a Gaussian could be of interest and is
Gaussian functions are analytic, and their limit as x → ∞ is 0 (for the above case of b = 0).
Gaussian functions are among those functions that are elementary but lack elementary antiderivatives; the integral of the Gaussian function is the error function. Nonetheless their improper integrals over the whole real line can be evaluated exactly, using the Gaussian integral
and one obtains
This integral is 1 if and only if
These Gaussians are plotted in the accompanying figure.
Gaussian functions centered at zero minimize the Fourier uncertainty principle.
The product of two Gaussian functions is a Gaussian, and the convolution of two Gaussian functions is also a Gaussian, with variance being the sum of the original variances:
Taking the Fourier transform (unitary, angular frequency convention) of a Gaussian function with parameters a = 1, b = 0 and c yields another Gaussian function, with parameters
The fact that the Gaussian function is an eigenfunction of the continuous Fourier transform allows us to derive the following interesting identity from the Poisson summation formula:
Integral of a Gaussian function
The integral of an arbitrary Gaussian function is
An alternative form is
where f must be strictly positive for the integral to converge.
Proof
The integral
for some real constants a, b, c > 0 can be calculated by putting it into the form of a Gaussian integral. First, the constant a can simply be factored out of the integral. Next, the variable of integration is changed from x to y = x - b.
and then to
Then, using the Gaussian integral identity
we have
Two-dimensional Gaussian function
In two dimensions, the power to which e is raised in the Gaussian function is any negative-definite quadratic form. Consequently, the level sets of the Gaussian will always be ellipses.
A particular example of a two-dimensional Gaussian function is
Here the coefficient A is the amplitude, xo,yo is the center and σx, σy are the x and y spreads of the blob. The figure on the right was created using A = 1, xo = 0, yo = 0, σx = σy = 1.
The volume under the Gaussian function is given by
In general, a two-dimensional elliptical Gaussian function is expressed as
where the matrix
is positive-definite.
Using this formulation, the figure on the right can be created using A = 1, (xo, yo) = (0, 0), a = c = 1/2, b = 0.
Meaning of parameters for the general equation
For the general form of the equation the coefficient A is the height of the peak and (xo, yo) is the center of the blob.
If we set
then we rotate the blob by a clockwise angle
Using the following Octave code one can easily see the effect of changing the parameters
Such functions are often used in image processing and in computational models of visual system function—see the articles on scale space and affine shn.
Also see multivariate normal distribution.
Higher-order Gaussian or Super-Gaussian function
A more general formulation of a Gaussian function with a flat-top and Gaussian fall-off can be taken by raising the content of the exponent to a power,
Multi-dimensional Gaussian function
In an
where
The integral of this Gaussian function over the whole
It can be easily calculated by diagonalizing the matrix
More generally a shifted Gaussian function is defined as
where
Gaussian profile estimation
A number of fields such as stellar photometry, Gaussian beam characterization, and emission/absorption line spectroscopy work with sampled Gaussian functions and need to accurately estimate the height, position, and width parameters of the function. These are
Once one has an algorithm for estimating the Gaussian function parameters, it is also important to know how accurate those estimates are. While an estimation algorithm can provide numerical estimates for the variance of each parameter (i.e. the variance of the estimated height, position, and width of the function), one can use Cramér–Rao bound theory to obtain an analytical expression for the lower bound on the parameter variances, given some assumptions about the data.
- The noise in the measured profile is either i.i.d. Gaussian, or the noise is Poisson-distributed.
- The spacing between each sampling (i.e. the distance between pixels measuring the data) is uniform.
- The peak is "well-sampled", so that less than 10% of the area or volume under the peak (area if a 1D Gaussian, volume if a 2D Gaussian) lies outside the measurement region.
- The width of the peak is much larger than the distance between sample locations (i.e. the detector pixels must be at least 5 times smaller than the Gaussian FWHM).
When these assumptions are satisfied, the following covariance matrix K applies for the 1D profile parameters
where
and in the Poisson noise case,
For the 2D profile parameters giving the amplitude
where the individual parameter variances are given by the diagonal elements of the covariance matrix.
Discrete Gaussian
One may ask for a discrete analog to the Gaussian; this is necessary in discrete applications, particularly digital signal processing. A simple answer is to sample the continuous Gaussian, yielding the sampled Gaussian kernel. However, this discrete function does not have the discrete analogs of the properties of the continuous function, and can lead to undesired effects, as described in the article scale space implementation.
An alternative approach is to use discrete Gaussian kernel:
where
This is the discrete analog of the continuous Gaussian in that it is the solution to the discrete diffusion equation (discrete space, continuous time), just as the continuous Gaussian is the solution to the continuous diffusion equation.
Applications
Gaussian functions appear in many contexts in the natural sciences, the social sciences, mathematics, and engineering. Some examples include:
