 | ||
In mathematics, an exponential function is a function of the form
Contents
- Formal definition
- Overview
- Derivatives and differential equations
- Continued fractions for ex
- Complex plane
- Computation of ab where both a and b are complex
- Matrices and Banach algebras
- Lie algebras
- Similar properties of e and the function ez
- exp and expm1
- References
in which the input variable x occurs as an exponent. A function of the form
As a functions of a real variable, exponential functions are uniquely characterized by the fact that the growth rate of such a function (i.e., its derivative) is directly proportional to the value of the function. The constant of proportionality of this relationship is the natural logarithm of the base
The constant e ≈ 2.71828... is the unique base for which the constant of proportionality is 1, so that the function's derivative is itself:
Since changing the base of the exponential function merely results in the appearance of an additional constant factor, it is computationally convenient to reduce the study of exponential functions in mathematical analysis to the study of this particular function, conventionally called the "natural exponential function", or simply, "the exponential function" and denoted by
The exponential function satisfies the fundamental multiplicative identity
(In fact, this identity extends to complex-valued exponents.) It can be shown that complete set of continuous, nonzero solutions of the functional equation
The argument of the exponential function can be any real or complex number or even an entirely different kind of mathematical object (e.g., a matrix).
Its ubiquitous occurrence in pure and applied mathematics has led mathematician W. Rudin to opine that the exponential function is "the most important function in mathematics". In applied settings, exponential functions model a relationship in which a constant change in the independent variable gives the same proportional change (i.e. percentage increase or decrease) in the dependent variable. Such a situation occurs widely in the natural and social sciences; thus, the exponential function also appears in variety of contexts within physics, chemistry, engineering, mathematical biology, and economics.
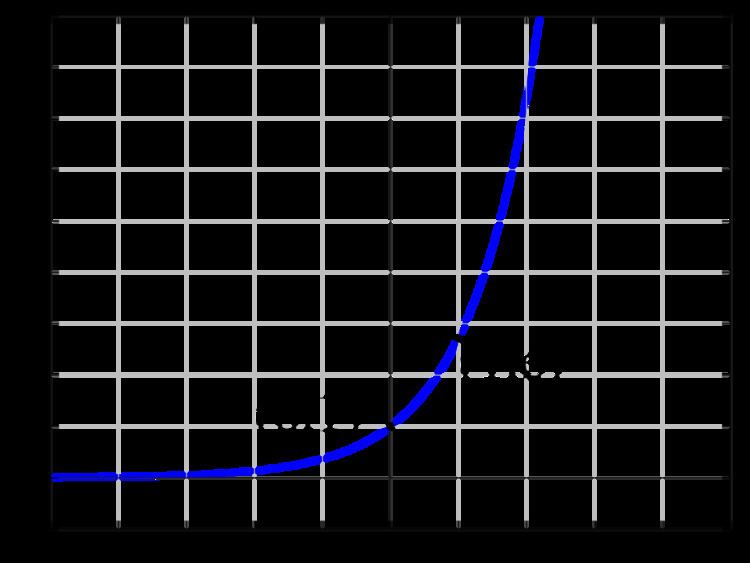
The graph of
Formal definition
The exponential function
Since the radius of convergence of this power series is infinite, this definition is applicable to all complex numbers
Less commonly, the real exponential function is defined as the solution y to the equation
The exponential function can also be defined as the following limit:
Overview
The exponential function arises whenever a quantity grows or decays at a rate proportional to its current value. One such situation is continuously compounded interest, and in fact it was this observation that led Jacob Bernoulli in 1683 to the number
now known as e. Later, in 1697, Johann Bernoulli studied the calculus of the exponential function.
If a principal amount of 1 earns interest at an annual rate of x compounded monthly, then the interest earned each month is x/12 times the current value, so each month the total value is multiplied by (1 + x/12), and the value at the end of the year is (1 + x/12)12. If instead interest is compounded daily, this becomes (1 + x/365)365. Letting the number of time intervals per year grow without bound leads to the limit definition of the exponential function,
first given by Euler. This is one of a number of characterizations of the exponential function; others involve series or differential equations.
From any of these definitions it can be shown that the exponential function obeys the basic exponentiation identity,
which is why it can be written as ex.
The derivative (rate of change) of the exponential function is the exponential function itself. More generally, a function with a rate of change proportional to the function itself (rather than equal to it) is expressible in terms of the exponential function. This function property leads to exponential growth and exponential decay.
The exponential function extends to an entire function on the complex plane. Euler's formula relates its values at purely imaginary arguments to trigonometric functions. The exponential function also has analogues for which the argument is a matrix, or even an element of a Banach algebra or a Lie algebra.
Derivatives and differential equations
The importance of the exponential function in mathematics and the sciences stems mainly from properties of its derivative. In particular,
Proof:
That is, ex is its own derivative and hence is a simple example of a Pfaffian function. Functions of the form cex for constant c are the only functions with that property (by the Picard–Lindelöf theorem). Other ways of saying the same thing include:
If a variable's growth or decay rate is proportional to its size—as is the case in unlimited population growth (see Malthusian catastrophe), continuously compounded interest, or radioactive decay—then the variable can be written as a constant times an exponential function of time. Explicitly for any real constant k, a function f: R → R satisfies f′ = kf if and only if f(x) = cekx for some constant c.
Furthermore, for any differentiable function f(x), we find, by the chain rule:
Continued fractions for ex
A continued fraction for ex can be obtained via an identity of Euler:
The following generalized continued fraction for ez converges more quickly:
or, by applying the substitution z = x/y:
with a special case for z = 2:
This formula also converges, though more slowly, for z > 2. For example:
Complex plane
As in the real case, the exponential function can be defined on the complex plane in several equivalent forms. The most common definition of the complex exponential function parallels the power series definition for real arguments, where the real variable is replaced by a complex one:
Termwise multiplication of two copies of these power series in the Cauchy sense, permitted by Mertens' theorem, shows that the defining multiplicative property of exponential functions continues to hold for all complex arguments:
The definition of the complex exponential function in turn leads to the appropriate definitions extending the trigonometric functions to complex arguments. In particular, when
In this expansion, the rearrangement of the terms into real and imaginary parts is justified by the absolute convergence of the series. The real and imaginary parts of the above expression in fact correspond to the series expansions of
The functions exp, cos, and sin so defined have infinite radii of convergence by the ratio test and are therefore entire functions (i.e., holomorphic on
These definitions for the exponential and trigonometric functions lead trivially to Euler's formula:
We could alternatively define the complex exponential function based on this relationship. If
where exp, cos, and sin on the right-hand side of the definition sign are to be interpreted as functions of a real variable, previously defined by other means.
For
The complex exponential function is periodic with period
When its domain is extended from the real line to the complex plane, the exponential function retains the following properties:
for all
Extending the natural logarithm to complex arguments yields the complex logarithm log z, which is a multivalued function.
We can then define a more general exponentiation:
for all complex numbers z and w. This is also a multivalued function, even when z is real. This distinction is problematic, as the multivalued functions log z and zw are easily confused with their single-valued equivalents when substituting a real number for z. The rule about multiplying exponents for the case of positive real numbers must be modified in a multivalued context:
(ez)w≠ ezw, but rather (ez)w
= e(z + 2πin)w multivalued over integers n
See failure of power and logarithm identities for more about problems with combining powers.
The exponential function maps any line in the complex plane to a logarithmic spiral in the complex plane with the center at the origin. Two special cases might be noted: when the original line is parallel to the real axis, the resulting spiral never closes in on itself; when the original line is parallel to the imaginary axis, the resulting spiral is a circle of some radius.
Computation of ab where both a and b are complex
Complex exponentiation ab can be defined by converting a to polar coordinates and using the identity (eln(a))b
= ab:
However, when b is not an integer, this function is multivalued, because θ is not unique (see failure of power and logarithm identities).
Matrices and Banach algebras
The power series definition of the exponential function makes sense for square matrices (for which the function is called the matrix exponential) and more generally in any Banach algebra B. In this setting, e0 = 1, and ex is invertible with inverse e−x for any x in B. If xy = yx, then ex + y = exey, but this identity can fail for noncommuting x and y.
Some alternative definitions lead to the same function. For instance, ex can be defined as
Or ex can be defined as f(1), where f: R→B is the solution to the differential equation f ′(t) = xf(t) with initial condition f(0) = 1.
Lie algebras
Given a Lie group G and its associated Lie algebra
The identity exp(x + y) = exp(x)exp(y) can fail for Lie algebra elements x and y that do not commute; the Baker–Campbell–Hausdorff formula supplies the necessary correction terms.
Similar properties of e and the function ez
The function ez is not in C(z) (i.e., is not the quotient of two polynomials with complex coefficients).
For n distinct complex numbers {a1, …, an}, the set {ea1z, …, eanz} is linearly independent over C(z).
The function ez is transcendental over C(z).
exp and expm1
Some calculators provide a dedicated exp(x) function designed to provide a higher precision than achievable by using ex directly.
Based on a proposal by William Kahan and first implemented in the Hewlett-Packard HP-41C calculator in 1979, some scientific calculators, computer algebra systems and programming languages (for example C99) support a special exponential minus 1 function alternatively named E^X-1, expm1(x), expm(x), or exp1m(x) to provide more accurate results for values of x near zero compared to using exp(x)-1 directly. This function is implemented using a different internal algorithm to avoid an intermediate result near 1, thereby allowing both the argument and the result to be near zero. Similar inverse functions named lnp1(x), ln1p(x) or log1p(x) exist as well.
