 | ||
In algebra, a quadratic function, a quadratic polynomial, a polynomial of degree 2, or simply a quadratic, is a polynomial function in one or more variables in which the highest-degree term is of the second degree. For example, a quadratic function in three variables x, y, and z contains exclusively terms x2, y2, z2, xy, xz, yz, x, y, z, and a constant:
Contents
- Etymology
- Coefficients
- Degree
- Variables
- The one variable case
- Bivariate case
- Forms of a univariate quadratic function
- Graph of the univariate function
- Vertex
- Maximum and minimum points
- Exact roots
- Upper bound on the magnitude of the roots
- The square root of a univariate quadratic function
- Iteration
- Bivariate two variable quadratic function
- Minimummaximum
- References
with at least one of the coefficients a, b, c, d, e, or f of the second-degree terms being non-zero.
A univariate (single-variable) quadratic function has the form
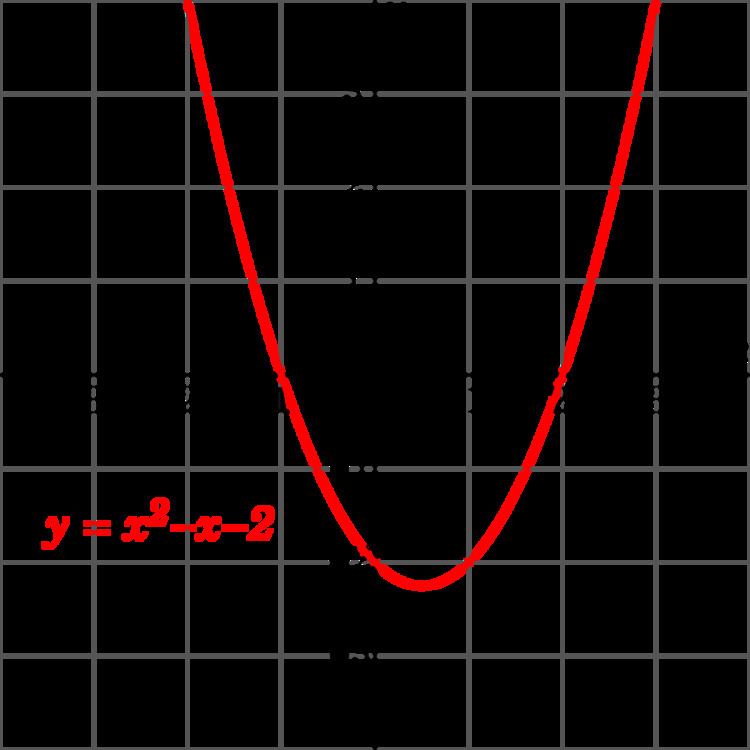
in the single variable x. The graph of a univariate quadratic function is a parabola whose axis of symmetry is parallel to the y-axis, as shown at right.
If the quadratic function is set equal to zero, then the result is a quadratic equation. The solutions to the univariate equation are called the roots of the univariate function.
The bivariate case in terms of variables x and y has the form
with at least one of a, b, c not equal to zero, and an equation setting this function equal to zero gives rise to a conic section (a circle or other ellipse, a parabola, or a hyperbola).
In general there can be an arbitrarily large number of variables, in which case the resulting surface is called a quadric, but the highest degree term must be of degree 2, such as x2, xy, yz, etc.
Etymology
The adjective quadratic comes from the Latin word quadrātum ("square"). A term like x2 is called a square in algebra because it is the area of a square with side x.
In general, a prefix quadr(i)- indicates the number 4. Examples are quadrilateral and quadrant. Quadratum is the Latin word for square.
Coefficients
The coefficients of a polynomial are often taken to be real or complex numbers, but in fact, a polynomial may be defined over any ring.
Degree
When using the term "quadratic polynomial", authors sometimes mean "having degree exactly 2", and sometimes "having degree at most 2". If the degree is less than 2, this may be called a "degenerate case". Usually the context will establish which of the two is meant.
Sometimes the word "order" is used with the meaning of "degree", e.g. a second-order polynomial.
Variables
A quadratic polynomial may involve a single variable x (the univariate case), or multiple variables such as x, y, and z (the multivariate case).
The one-variable case
Any single-variable quadratic polynomial may be written as
where x is the variable, and a, b, and c represent the coefficients. In elementary algebra, such polynomials often arise in the form of a quadratic equation
Bivariate case
Any quadratic polynomial with two variables may be written as
where x and y are the variables and a, b, c, d, e, and f are the coefficients. Such polynomials are fundamental to the study of conic sections, which are characterized by equating the expression for f (x, y) to zero. Similarly, quadratic polynomials with three or more variables correspond to quadric surfaces and hypersurfaces. In linear algebra, quadratic polynomials can be generalized to the notion of a quadratic form on a vector space.
Forms of a univariate quadratic function
A univariate quadratic function can be expressed in three formats:
The coefficient a is the same value in all three forms. To convert the standard form to factored form, one needs only the quadratic formula to determine the two roots r1 and r2. To convert the standard form to vertex form, one needs a process called completing the square. To convert the factored form (or vertex form) to standard form, one needs to multiply, expand and/or distribute the factors.
Graph of the univariate function
Regardless of the format, the graph of a univariate quadratic function
The coefficient a controls the degree of curvature of the graph; a larger magnitude of a gives the graph a more closed (sharply curved) appearance.
The coefficients b and a together control the location of the axis of symmetry of the parabola (also the x-coordinate of the vertex) which is at
The coefficient c controls the height of the parabola; more specifically, it is the height of the parabola where it intercepts the y-axis.
Vertex
The vertex of a parabola is the place where it turns; hence, it is also called the turning point. If the quadratic function is in vertex form, the vertex is (h, k). Using the method of completing the square, one can turn the standard form
into
so the vertex, (h, k), of the parabola in standard form is
If the quadratic function is in factored form
the average of the two roots, i.e.,
is the x-coordinate of the vertex, and hence the vertex (h, k) is
The vertex is also the maximum point if a < 0, or the minimum point if a > 0.
The vertical line
that passes through the vertex is also the axis of symmetry of the parabola.
Maximum and minimum points
Using calculus, the vertex point, being a maximum or minimum of the function, can be obtained by finding the roots of the derivative:
x is a root of f '(x) if f '(x) = 0 resulting in
with the corresponding function value
so again the vertex point coordinates, (h, k), can be expressed as
Exact roots
The roots (or zeros), r1 and r2, of the univariate quadratic function
are the values of x for which f(x) = 0.
When the coefficients a, b, and c, are real or complex, the roots are
Upper bound on the magnitude of the roots
The modulus of the roots of a quadratic
The square root of a univariate quadratic function
The square root of a univariate quadratic function gives rise to one of the four conic sections, almost always either to an ellipse or to a hyperbola.
If
If
Iteration
To iterate a function
One cannot always deduce the analytic form of
For example, for the iterative equation
one has
where
So by induction,
can be obtained, where
Finally, we have
as the solution.
See Topological conjugacy for more detail about the relationship between f and g. And see Complex quadratic polynomial for the chaotic behavior in the general iteration.
The logistic map
with parameter 2<r<4 can be solved in certain cases, one of which is chaotic and one of which is not. In the chaotic case r=4 the solution is
where the initial condition parameter
The solution of the logistic map when r=2 is
for
Bivariate (two variable) quadratic function
A bivariate quadratic function is a second-degree polynomial of the form
where A, B, C, D, and E are fixed coefficients and F is the constant term. Such a function describes a quadratic surface. Setting
Minimum/maximum
If
If
If
If
