 | ||
In mathematics, the gradient is a multi-variable generalization of the derivative. While a derivative can be defined on functions of a single variable, for functions of several variables, the gradient takes its place. The gradient is a vector-valued function, as opposed to a derivative, which is scalar-valued. If f(x1, ..., xn) is a differentiable, real-valued function of several variables, its gradient is the vector whose components are the n partial derivatives of f.
Contents
- Motivation
- Definition
- Cartesian coordinates
- Cylindrical and spherical coordinates
- Linear approximation to a function
- Differential or exterior derivative
- Gradient as a derivative
- Linearity
- Product rule
- Chain rule
- Level sets
- Conservative vector fields and the gradient theorem
- Riemannian manifolds
- Gradient of a vector
- References
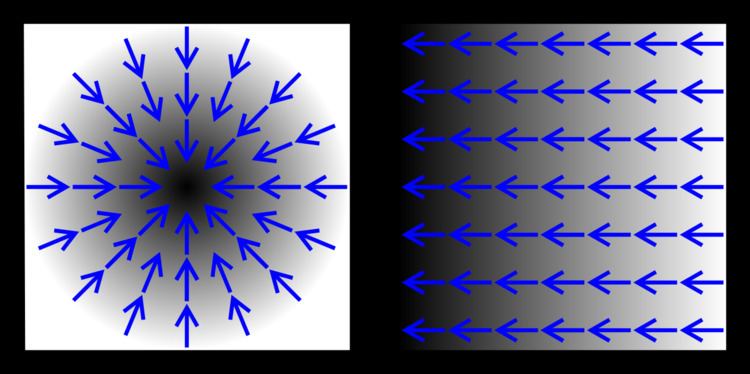
Like the derivative, the gradient represents the slope of the tangent of the graph of the function. More precisely, the gradient points in the direction of the greatest rate of increase of the function, and its magnitude is the slope of the graph in that direction. The components of the gradient in coordinates are the coefficients of the variables in the equation of the tangent space to the graph. This characterizing property of the gradient allows it to be defined independently of a choice of coordinate system, as a vector field whose components in a coordinate system will transform when going from one coordinate system to another.
The Jacobian is the generalization of the gradient for vector-valued functions of several variables and differentiable maps between Euclidean spaces or, more generally, manifolds. A further generalization for a function between Banach spaces is the Fréchet derivative.
Motivation
Consider a room in which the temperature is given by a scalar field, T, so at each point (x, y, z) the temperature is T(x, y, z). (Assume that the temperature does not change over time.) At each point in the room, the gradient of T at that point will show the direction in which the temperature rises most quickly. The magnitude of the gradient will determine how fast the temperature rises in that direction.
Consider a surface whose height above sea level at point (x, y) is H(x, y). The gradient of H at a point is a vector pointing in the direction of the steepest slope or grade at that point. The steepness of the slope at that point is given by the magnitude of the gradient vector.
The gradient can also be used to measure how a scalar field changes in other directions, rather than just the direction of greatest change, by taking a dot product. Suppose that the steepest slope on a hill is 40%. If a road goes directly up the hill, then the steepest slope on the road will also be 40%. If, instead, the road goes around the hill at an angle, then it will have a shallower slope. For example, if the angle between the road and the uphill direction, projected onto the horizontal plane, is 60°, then the steepest slope along the road will be 20%, which is 40% times the cosine of 60°.
This observation can be mathematically stated as follows. If the hill height function H is differentiable, then the gradient of H dotted with a unit vector gives the slope of the hill in the direction of the vector. More precisely, when H is differentiable, the dot product of the gradient of H with a given unit vector is equal to the directional derivative of H in the direction of that unit vector.
Definition
The gradient (or gradient vector field) of a scalar function f(x1, x2, x3,... xn) is denoted ∇f or ∇→f where ∇ (the nabla symbol) denotes the vector differential operator, del. The notation grad f is also commonly used for the gradient. The gradient of f is defined as the unique vector field whose dot product with any vector v at each point x is the directional derivative of f along v. That is,
In a rectangular coordinate system, the gradient is the vector field whose components are the partial derivatives of f:
where the ei are the orthogonal unit vectors pointing in the coordinate directions. When a function also depends on a parameter such as time, the gradient often refers simply to the vector of its spatial derivatives only (see Spatial gradient).
Cartesian coordinates
In the three-dimensional Cartesian coordinate system, the gradient is given by:
where i, j, k are the standard unit vectors. For example, the gradient of the function
is
In some applications it is customary to represent the gradient as a row vector or column vector of its components in a rectangular coordinate system.
Cylindrical and spherical coordinates
In cylindrical coordinates, the gradient is given by:
where φ is the azimuthal or azmuth angle, z is the axial coordinate, and eρ, eφ and ez are unit vectors pointing along the coordinate directions.
In spherical coordinates, the gradient is given by:
where φ is the azimuth angle and θ is the zenith angle.
For the gradient in other orthogonal coordinate systems, see Orthogonal coordinates (Differential operators in three dimensions).
Linear approximation to a function
The gradient of a function f from the Euclidean space ℝn to ℝ at any particular point x0 in ℝn characterizes the best linear approximation to f at x0. The approximation is as follows:
for x close to x0, where (∇f )x0 is the gradient of f computed at x0, and the dot denotes the dot product on ℝn. This equation is equivalent to the first two terms in the multivariable Taylor series expansion of f at x0.
Differential or (exterior) derivative
The best linear approximation to a differentiable function
at a point x in ℝn is a linear map from ℝn to ℝ which is often denoted by dfx or Df(x) and called the differential or (total) derivative of f at x. The gradient is therefore related to the differential by the formula
for any v ∈ ℝn. The function df, which maps x to dfx, is called the differential or exterior derivative of f and is an example of a differential 1-form.
If ℝn is viewed as the space of (dimension n) column vectors (of real numbers), then one can regard df as the row vector with components
so that dfx(v) is given by matrix multiplication. The gradient is then the corresponding column vector, i.e.,
Gradient as a derivative
Let U be an open set in ℝn. If the function f : U → ℝ is differentiable, then the differential of f is the (Fréchet) derivative of f. Thus ∇f is a function from U to the space ℝ such that
where · is the dot product.
As a consequence, the usual properties of the derivative hold for the gradient:
Linearity
The gradient is linear in the sense that if f and g are two real-valued functions differentiable at the point a ∈ ℝn, and α and β are two constants, then αf + βg is differentiable at a, and moreover
Product rule
If f and g are real-valued functions differentiable at a point a ∈ ℝn, then the product rule asserts that the product fg is differentiable at a, and
Chain rule
Suppose that f : A → ℝ is a real-valued function defined on a subset A of ℝn, and that f is differentiable at a point a. There are two forms of the chain rule applying to the gradient. First, suppose that the function g is a parametric curve; that is, a function g : I → ℝn maps a subset I ⊂ ℝ into ℝn. If g is differentiable at a point c ∈ I such that g(c) = a, then
where ∘ is the composition operator: ( f ∘ g)(x) = f(g(x)).
More generally, if instead I ⊂ ℝk, then the following holds:
where (Dg)T denotes the transpose Jacobian matrix.
For the second form of the chain rule, suppose that h : I → ℝ is a real valued function on a subset I of ℝ, and that h is differentiable at the point f(a) ∈ I. Then
Level sets
A level surface, or isosurface, is the set of all points where some function has a given value.
If f is differentiable, then the dot product (∇f )x ⋅ v of the gradient at a point x with a vector v gives the directional derivative of f at x in the direction v. It follows that in this case the gradient of f is orthogonal to the level sets of f. For example, a level surface in three-dimensional space is defined by an equation of the form F(x, y, z) = c. The gradient of F is then normal to the surface.
More generally, any embedded hypersurface in a Riemannian manifold can be cut out by an equation of the form F(P) = 0 such that dF is nowhere zero. The gradient of F is then normal to the hypersurface.
Similarly, an affine algebraic hypersurface may be defined by an equation F(x1,... xn) = 0, where F is a polynomial. The gradient of F is zero at a singular point of the hypersurface (this is the definition of a singular point). At a non-singular point, it is a nonzero normal vector.
Conservative vector fields and the gradient theorem
The gradient of a function is called a gradient field. A (continuous) gradient field is always a conservative vector field: its line integral along any path depends only on the endpoints of the path, and can be evaluated by the gradient theorem (the fundamental theorem of calculus for line integrals). Conversely, a (continuous) conservative vector field is always the gradient of a function.
Riemannian manifolds
For any smooth function f on a Riemannian manifold (M,g), the gradient of f is the vector field ∇f such that for any vector field X,
where gx( , ) denotes the inner product of tangent vectors at x defined by the metric g and ∂X f (sometimes denoted X( f )) is the function that takes any point x ∈ M to the directional derivative of f in the direction X, evaluated at x. In other words, in a coordinate chart φ from an open subset of M to an open subset of ℝn, (∂X f )(x) is given by:
where Xj denotes the jth component of X in this coordinate chart.
So, the local form of the gradient takes the form:
Generalizing the case M = ℝn, the gradient of a function is related to its exterior derivative, since
More precisely, the gradient ∇f is the vector field associated to the differential 1-form df using the musical isomorphism
(called "sharp") defined by the metric g. The relation between the exterior derivative and the gradient of a function on ℝn is a special case of this in which the metric is the flat metric given by the dot product.
Gradient of a vector
Since the total derivative of a vector field is a linear mapping from vectors to vectors, it is a tensor quantity.
In rectangular coordinates, the gradient of a vector field f = ( f1, f2, f3) is defined by:
where the Einstein summation notation is used and the product of the vectors ei, ek is a dyadic tensor of type (2,0), or the Jacobian matrix
In curvilinear coordinates, or more generally on a curved manifold, the gradient involves Christoffel symbols:
where gjk are the components of the metric tensor and the ei are the coordinate vectors.
Expressed more invariantly, the gradient of a vector field f can be defined by the Levi-Civita connection and metric tensor:
where ∇c is the connection.
