Conservative vector field

Informal treatment

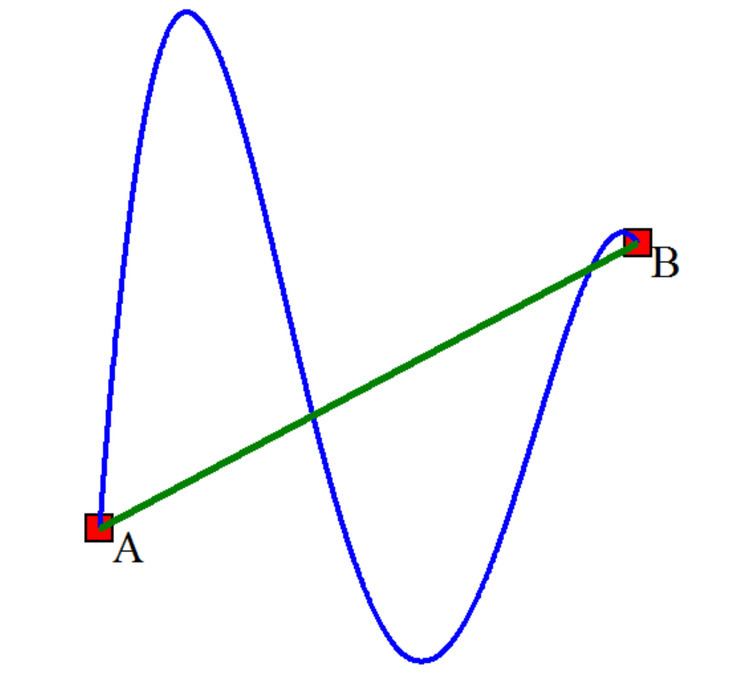
In a two- and three-dimensional space, there is an ambiguity in taking an integral between two points as there are infinitely many paths between the two points — apart from the straight line formed between the two points, one could choose a curved path of greater length as shown in the figure. Therefore, in general, the value of the integral depends on the path taken. However, in the special case of a conservative vector field, the value of the integral is independent of the path taken, which can be thought of as a large-scale cancellation of all elements d R that don't have a component along the straight line between the two points. To visualize this, imagine two people climbing a cliff; one decides to scale the cliff by going vertically up it, and the second decides to walk along a winding path that is longer in length than the height of the cliff, but at only a small angle to the horizontal. Although the two hikers have taken different routes to get up to the top of the cliff, at the top, they will have both gained the same amount of gravitational potential energy. This is because a gravitational field is conservative. As an example of a non-conservative field, imagine pushing a box from one end of a room to another. Pushing the box in a straight line across the room requires noticeably less work against friction than along a curved path covering a greater distance.

Intuitive explanation

M. C. Escher's painting Ascending and Descending illustrates a non-conservative vector field, impossibly made to appear to be the gradient of the varying height above ground as one moves along the staircase. It is rotational in that one can keep getting higher or keep getting lower while going around in circles. It is non-conservative in that one can return to one's starting point while ascending more than one descends or vice versa. On a real staircase, the height above the ground is a scalar potential field: If one returns to the same place, one goes upward exactly as much as one goes downward. Its gradient would be a conservative vector field and is irrotational. The situation depicted in the painting is impossible.

Definition

A vector field v : U → R n , where U is an open subset of R n , is said to be conservative if and only if there exists a C 1 scalar field φ on U such that

Here, ∇ φ denotes the gradient of φ . When the equation above holds, φ is called a scalar potential for v .

The Fundamental Theorem of Vector Calculus states that any vector field can be expressed as the sum of a conservative vector field and a solenoidal field.

Path independence

A key property of a conservative vector field v is that its integral along a path depends only on the endpoints of that path, not the particular route taken. Suppose that P is a rectifiable path in U with initial point A and terminal point B . If v = ∇ φ for some C 1 scalar field φ so that v is a conservative vector field, then the Gradient Theorem states that

This holds as a consequence of the Chain Rule and the Fundamental Theorem of Calculus.

An equivalent formulation of this is that

for every rectifiable simple closed path C in U . The converse of this statement is also true: If the circulation of v around every rectifiable simple closed path in U is 0 , then v is a conservative vector field.

Irrotational vector fields

Let n = 3 , and let v : U → R 3 be a C 1 vector field, with U open as always. Then v is called irrotational if and only if its curl is 0 everywhere in U , i.e., if

For this reason, such vector fields are sometimes referred to as curl-free vector fields or curl-less vector fields. They are also referred to as longitudinal vector fields.

It is an identity of vector calculus that for any C 2 scalar field φ on U , we have

Therefore, every C 1 conservative vector field on U is also an irrotational vector field on U .

Provided that U is simply connected, the converse of this is also true: Every irrotational vector field on U is a C 1 conservative vector field on U .

The above statement is not true in general if U is not simply connected. Let U be R 3 with the z -axis removed, i.e., U = R 3 ∖ { ( 0 , 0 , z ) ∣ z ∈ R } . Now, define a vector field v on U by

Then v has zero curl everywhere in U , i.e., v is irrotational. However, the circulation of v around the unit circle in the x y -plane is 2 π . Indeed, note that in polar coordinates, v = e ϕ / r , so the integral over the unit circle is

Therefore, v does not have the path-independence property discussed above and is not conservative. (However, in any simply connected open sub-region of U , it is still true that v is conservative. In fact, the field above is the gradient of arg ⁡ ( x + i y ) . As we know from complex analysis, this is a multi-valued function that requires a branch cut from the origin to ∞ to be defined in a continuous manner. Hence, in a region that does not go around the z -axis, its gradient is conservative.)

In a simply connected open region, an irrotational vector field has the path-independence property. This can be seen by noting that in such a region, an irrotational vector field is conservative, and conservative vector fields have the path-independence property. The result can also be proved directly by using Stokes' theorem. In a simply connected open region, any vector field that has the path-independence property must also be irrotational.

More abstractly, in the presence of a Riemannian metric, vector fields correspond to differential 1 -forms. The conservative vector fields correspond to the exact 1 -forms, that is, to the forms which are the exterior derivative d ϕ of a function (scalar field) ϕ on U . The irrotational vector fields correspond to the closed 1 -forms, that is, to the 1 -forms ω such that d ω = 0 . As d 2 = 0 , any exact form is closed, so any conservative vector field is irrotational. Conversely, all closed 1 -forms are exact if and only if U is simply connected. To see why, note that being simply connected means that the fundamental group of U vanishes. Because U is an open subset of R 2 , any loop may be straightened to a finite polygonal path, and since such paths have only finitely many self-intersections, the loop is a union of finitely many simple closed curves. It follows that the fundamental group vanishes if and only if the first singular homology group H 1 ( U , Z ) vanishes. It also follows that H 1 ( U , Z ) is generated by the classes of simple closed curves and is therefore torsion-free. Hence by the universal coefficient theorem, the singular homology group vanishes if and only if the singular cohomology group H 1 ( U , R ) vanishes. By de Rham's theorem, the latter group is isomorphic to the first de Rham cohomology group H d R 1 ( U ) . Consequently, U is simply connected if and only if all closed 1 -forms are exact.

Irrotational flows

The flow velocity v of a fluid is a vector field, and the vorticity ω of the flow can be defined by

A common alternative notation for vorticity is ζ .

If v is irrotational, with ∇ × v ≡ 0 , then the flow is said to be an irrotational flow. The vorticity of an irrotational flow is zero.

Kelvin's circulation theorem states that a fluid that is irrotational in an inviscid flow will remain irrotational. This result can be derived from the vorticity transport equation, obtained by taking the curl of the Navier-Stokes Equations.

For a two-dimensional flow, the vorticity acts as a measure of the local rotation of fluid elements. Note that the vorticity does not imply anything about the global behavior of a fluid. It is possible for a fluid traveling in a straight line to have vorticity, and it is possible for a fluid that moves in a circle to be irrotational.

Conservative forces

If the vector field associated to a force F is conservative, then the force is said to be a conservative force.

The most prominent examples of conservative forces are the gravitational force and the electric force associated to an electrostatic field. According to Newton's law of gravitation, the gravitational force F G acting on a mass m due to a mass M , which is a distance r between them, obeys the equation

where G is the gravitational constant and r ^ is a unit vector pointing from M toward m . The force of gravity is conservative because F G = − ∇ Φ G , where

is the gravitational potential energy.

For conservative forces, path independence can be interpreted to mean that the work done in going from a point A to a point B is independent of the path chosen, and that the work W done in going around a simple closed loop is 0 :

The total energy of a particle moving under the influence of conservative forces is conserved, in the sense that a loss of potential energy is converted to an equal quantity of kinetic energy, or vice versa.