Directional derivative

Definition

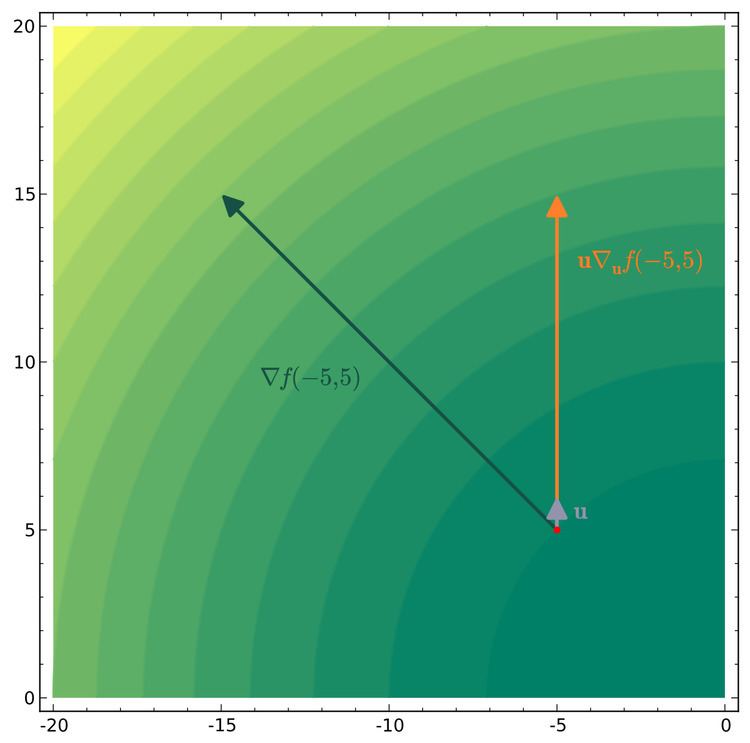
The directional derivative of a scalar function

along a vector

is the function defined by the limit

In the context of a function on a Euclidean space, some texts restrict the vector v to being a unit vector. Without the restriction, this definition is valid in a broad range of contexts, for example where the norm of a vector (and hence a unit vector) is undefined.

If the function f is differentiable at x, then the directional derivative exists along any vector v, and one has

where the ∇ on the right denotes the gradient and ⋅ is the dot product. Intuitively, the directional derivative of f at a point x represents the rate of change of f with respect to time when moving past x at velocity v.

Variation using only direction of vector for Euclidean space

Some authors define the directional derivative to be with respect to an arbitrary nonzero vector v after normalization, thus being independent of its magnitude and depending only on its direction.

This definition gives the rate of increase of f per unit of distance moved in the given direction. In this case, one has

or in case f is differentiable at x,

Notation

Directional derivatives can be also denoted by:

where v is a parameterization of a curve to which v is tangent and which determines its magnitude.

Properties

Many of the familiar properties of the ordinary derivative hold for the directional derivative. These include, for any functions f and g defined in a neighborhood of, and differentiable at, p:

In differential geometry

Let M be a differentiable manifold and p a point of M. Suppose that f is a function defined in a neighborhood of p, and differentiable at p. If v is a tangent vector to M at p, then the directional derivative of f along v, denoted variously as df(v) (see Exterior derivative), ∇ v f ( p ) (see Covariant derivative), L v f ( p ) (see Lie derivative), or v p ( f ) (see Tangent space § Definition via derivations), can be defined as follows. Let γ : [−1, 1] → M be a differentiable curve with γ(0) = p and γ′(0) = v. Then the directional derivative is defined by

This definition can be proven independent of the choice of γ, provided γ is selected in the prescribed manner so that γ′(0) = v.

The Lie derivative

The Lie derivative of a vector field W μ ( x ) along a vector field V μ ( x ) is given by the difference of two directional derivatives (with vanishing torsion):

In particular, for a scalar field ϕ ( x ) , the Lie derivative reduces to the standard directional derivative:

The Riemann tensor

Directional derivatives are often used in introductory derivations of the Riemann curvature tensor. Consider a curved rectangle with an infinitesimal vector δ along one edge and δ′ along the other. We translate a covector S along δ then δ′ and then subtract the translation along δ′ and then δ. Instead of building the directional derivative using partial derivatives, we use the covariant derivative. The translation operator for δ is thus

and for δ′

The difference between the two paths is then

It can be argued that the noncommutativity of the covariant derivatives measures the curvature of the manifold:

with R the Riemann tensor of course and the sign depending on the sign convention of the author.

Translations

In the Poincaré algebra, we can define an infinitesimal translation operator P as

(the i ensures that P is a self-adjoint operator) For a finite displacement λ, the unitary Hilbert space representation for translations is

By using the above definition of the infinitesimal translation operator, we see that the finite translation operator is an exponentiated directional derivative:

This is a translation operator in the sense that it acts on multivariable functions f(x) as

Rotations

The rotation operator also contains a directional derivative. The rotation operator for an angle θ, i.e. by an amount θ=|θ| about an axis parallel to θ ^ =θ/θ is

Here L is the vector operator that generates SO(3):

It may be shown geometrically that an infinitesimal right-handed rotation changes the position vector x by

So we would expect under infinitesimal rotation:

It follows that

Following the same exponentiation procedure as above, we arrive at the rotation operator in the position basis, which is an exponentiated directional derivative:

Normal derivative

A normal derivative is a directional derivative taken in the direction normal (that is, orthogonal) to some surface in space, or more generally along a normal vector field orthogonal to some hypersurface. See for example Neumann boundary condition. If the normal direction is denoted by n , then the directional derivative of a function f is sometimes denoted as ∂ f ∂ n . In other notations

In the continuum mechanics of solids

Several important results in continuum mechanics require the derivatives of vectors with respect to vectors and of tensors with respect to vectors and tensors. The directional directive provides a systematic way of finding these derivatives.

The definitions of directional derivatives for various situations are given below. It is assumed that the functions are sufficiently smooth that derivatives can be taken.

Derivatives of scalar valued functions of vectors

Let f ( v ) be a real valued function of the vector v . Then the derivative of f ( v ) with respect to v (or at v ) in the direction u is defined as

for all vectors u .

Properties:

Derivatives of vector valued functions of vectors

Let f ( v ) be a vector valued function of the vector v . Then the derivative of f ( v ) with respect to v (or at v ) in the direction u is the second-order tensor defined as

for all vectors u .

Properties:

Derivatives of scalar valued functions of second-order tensors

Let f ( S ) be a real valued function of the second order tensor S . Then the derivative of f ( S ) with respect to S (or at S ) in the direction T is the second order tensor defined as

for all second order tensors T .

Properties:

Derivatives of tensor valued functions of second-order tensors

Let F ( S ) be a second order tensor valued function of the second order tensor S . Then the derivative of F ( S ) with respect to S (or at S ) in the direction T is the fourth order tensor defined as

for all second order tensors T .

Properties: