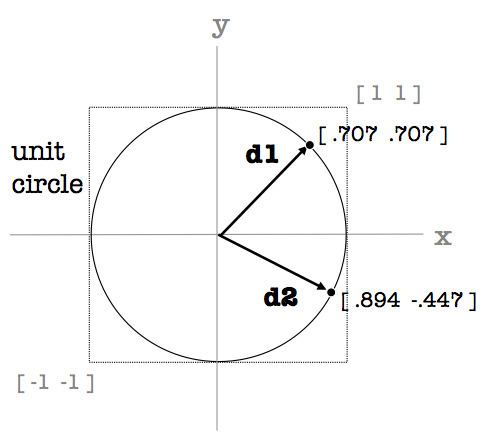
Unit vector - Alchetron, The Free Social Encyclopedia

In mathematics, a unit vector in a normed vector space is a vector (often a spatial vector) of length 1. A unit vector is often denoted by a lowercase letter with a circumflex, or "hat": ı ^ (pronounced "i-hat"). The term direction vector is used to describe a unit vector being used to represent spatial direction, and such quantities are commonly denoted as d. Two 2D direction vectors, d1 and d2 are illustrated. 2D spatial directions represented this way are equivalent numerically to points on the unit circle.

By definition, in a Euclidean space the dot product of two unit vectors is a scalar value amounting to the cosine of the smaller subtended angle. In three-dimensional Euclidean space, the cross product of two arbitrary unit vectors is a 3rd vector orthogonal to both of them having length equal to the sine of the smaller subtended angle. The normalized cross product corrects for this varying length, and yields the mutually orthogonal unit vector to the two inputs, applying the right-hand rule to resolve one of two possible directions.

Cartesian coordinates

Unit vectors may be used to represent the axes of a Cartesian coordinate system. For instance, the unit vectors in the direction of the x, y, and z axes of a three dimensional Cartesian coordinate system are

i ^ = [ 1 0 0 ] , j ^ = [ 0 1 0 ] , k ^ = [ 0 0 1 ]

They are sometimes referred to as the versors of the coordinate system, and they form a set of mutually orthogonal unit vectors, typically referred to as a standard basis in linear algebra.

They are often denoted using normal vector notation (e.g., i or ı → ) rather than standard unit vector notation (e.g., ı ^ ). In most contexts it can be assumed that i, j, and k, (or ı → , ȷ → , and k → ) are versors of a 3-D Cartesian coordinate system. The notations ( x ^ , y ^ , z ^ ) , ( x ^ 1 , x ^ 2 , x ^ 3 ) , ( e ^ x , e ^ y , e ^ z ) , or ( e ^ 1 , e ^ 2 , e ^ 3 ) , with or without hat, are also used, particularly in contexts where i, j, k might lead to confusion with another quantity (for instance with index symbols such as i, j, k, used to identify an element of a set or array or sequence of variables).

When a unit vector in space is expressed, with Cartesian notation, as a linear combination of i, j, k, its three scalar components can be referred to as direction cosines. The value of each component is equal to the cosine of the angle formed by the unit vector with the respective basis vector. This is one of the methods used to describe the orientation (angular position) of a straight line, segment of straight line, oriented axis, or segment of oriented axis (vector).

Cylindrical coordinates

The three orthogonal unit vectors appropriate to cylindrical symmetry are:

ρ ^ (also designated e ^ or s ^ ), representing the direction along which the distance of the point from the axis of symmetry is measured;

φ ^ , representing the direction of the motion that would be observed if the point were rotating counterclockwise about the symmetry axis;

z ^ , representing the direction of the symmetry axis;

They are related to the Cartesian basis x ^ , y ^ , z ^ by:

ρ ^ = cos ⁡ φ x ^ + sin ⁡ φ y ^ φ ^ = − sin ⁡ φ x ^ + cos ⁡ φ y ^ z ^ = z ^ .

It is important to note that ρ ^ and φ ^ are functions of φ , and are not constant in direction. When differentiating or integrating in cylindrical coordinates, these unit vectors themselves must also be operated on. For a more complete description, see Jacobian matrix. The derivatives with respect to φ are:

∂ ρ ^ ∂ φ = − sin ⁡ φ x ^ + cos ⁡ φ y ^ = φ ^ ∂ φ ^ ∂ φ = − cos ⁡ φ x ^ − sin ⁡ φ y ^ = − ρ ^ ∂ z ^ ∂ φ = 0 .

Spherical coordinates

The unit vectors appropriate to spherical symmetry are: r ^ , the direction in which the radial distance from the origin increases; φ ^ , the direction in which the angle in the x-y plane counterclockwise from the positive x-axis is increasing; and θ ^ , the direction in which the angle from the positive z axis is increasing. To minimize degeneracy, the polar angle is usually taken 0 ≤ θ ≤ 180 ∘ . It is especially important to note the context of any ordered triplet written in spherical coordinates, as the roles of φ ^ and θ ^ are often reversed. Here, the American "physics" convention is used. This leaves the azimuthal angle φ defined the same as in cylindrical coordinates. The Cartesian relations are:

r ^ = sin ⁡ θ cos ⁡ φ x ^ + sin ⁡ θ sin ⁡ φ y ^ + cos ⁡ θ z ^ θ ^ = cos ⁡ θ cos ⁡ φ x ^ + cos ⁡ θ sin ⁡ φ y ^ − sin ⁡ θ z ^ φ ^ = − sin ⁡ φ x ^ + cos ⁡ φ y ^

The spherical unit vectors depend on both φ and θ , and hence there are 5 possible non-zero derivatives. For a more complete description, see Jacobian matrix and determinant. The non-zero derivatives are:

∂ r ^ ∂ φ = − sin ⁡ θ sin ⁡ φ x ^ + sin ⁡ θ cos ⁡ φ y ^ = sin ⁡ θ φ ^ ∂ r ^ ∂ θ = cos ⁡ θ cos ⁡ φ x ^ + cos ⁡ θ sin ⁡ φ y ^ − sin ⁡ θ z ^ = θ ^ ∂ θ ^ ∂ φ = − cos ⁡ θ sin ⁡ φ x ^ + cos ⁡ θ cos ⁡ φ y ^ = cos ⁡ θ φ ^ ∂ θ ^ ∂ θ = − sin ⁡ θ cos ⁡ φ x ^ − sin ⁡ θ sin ⁡ φ y ^ − cos ⁡ θ z ^ = − r ^ ∂ φ ^ ∂ φ = − cos ⁡ φ x ^ − sin ⁡ φ y ^ = − sin ⁡ θ r ^ − cos ⁡ θ θ ^

General unit vectors

Common general themes of unit vectors occur throughout physics and geometry:

Curvilinear coordinates

In general, a coordinate system may be uniquely specified using a number of linearly independent unit vectors e ^ n equal to the degrees of freedom of the space. For ordinary 3-space, these vectors may be denoted e ^ 1 , e ^ 2 , e ^ 3 . It is nearly always convenient to define the system to be orthonormal and right-handed:

e ^ i ⋅ e ^ j = δ i j

e ^ i ⋅ ( e ^ j × e ^ k ) = ε i j k

where δ_ij is the Kronecker delta (which is one for i = j and zero else) and ε i j k is the Levi-Civita symbol (which is one for permutations ordered as ijk and minus one for permutations ordered as kji).

References

Unit vector Wikipedia

(Text) CC BY-SA