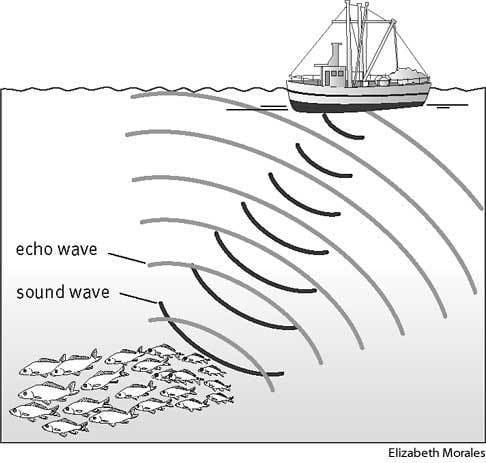
How sonar works
Sonar (originally an acronym for SOund Navigation And Ranging) is a technique that uses sound propagation (usually underwater, as in submarine navigation) to navigate, communicate with or detect objects on or under the surface of the water, such as other vessels. Two types of technology share the name "sonar": passive sonar is essentially listening for the sound made by vessels; active sonar is emitting pulses of sounds and listening for echoes. Sonar may be used as a means of acoustic location and of measurement of the echo characteristics of "targets" in the water. Acoustic location in air was used before the introduction of radar. Sonar may also be used in air for robot navigation, and SODAR (an upward looking in-air sonar) is used for atmospheric investigations. The term sonar is also used for the equipment used to generate and receive the sound. The acoustic frequencies used in sonar systems vary from very low (infrasonic) to extremely high (ultrasonic). The study of underwater sound is known as underwater acoustics or hydroacoustics.
Contents
- How sonar works
- Sonar class 9th science video lecture
- History
- ASDIC
- SONAR
- Materials and designs
- Active sonar
- Project Artemis
- Transponder
- Performance prediction
- Hand held sonar for use by a diver
- Passive sonar
- Identifying sound sources
- Noise limitations
- Performance factors
- Sound propagation
- Scattering
- Target characteristics
- Countermeasures
- Military applications
- Anti submarine warfare
- Torpedoes
- Mines
- Mine countermeasures
- Submarine navigation
- Aircraft
- Underwater communications
- Ocean surveillance
- Underwater security
- Hand held sonar
- Intercept sonar
- Fisheries
- Echo sounding
- Net location
- ROV and UUV
- Vehicle location
- Prosthesis for the visually impaired
- Biomass estimation
- Wave measurement
- Water velocity measurement
- Bottom type assessment
- Bathymetric mapping
- Sub bottom profiling
- Synthetic aperture sonar
- Parametric sonar
- Sonar in extraterrestrial contexts
- Effect on marine mammals
- Effect on fish
- Frequencies and resolutions
- References
Sonar class 9th science video lecture
History
Although some animals (dolphins and bats) have used sound for communication and object detection for millions of years, use by humans in the water is initially recorded by Leonardo da Vinci in 1490: a tube inserted into the water was said to be used to detect vessels by placing an ear to the tube.
In the 19th century an underwater bell was used as an ancillary to lighthouses to provide warning of hazards.
The use of sound to 'echo locate' underwater in the same way as bats use sound for aerial navigation seems to have been prompted by the Titanic disaster of 1912. The world's first patent for an underwater echo ranging device was filed at the British Patent Office by English meteorologist Lewis Richardson a month after the sinking of the Titanic, and a German physicist Alexander Behm obtained a patent for an echo sounder in 1913.
The Canadian engineer Reginald Fessenden, while working for the Submarine Signal Company in Boston, built an experimental system beginning in 1912, a system later tested in Boston Harbor, and finally in 1914 from the U.S. Revenue (now Coast Guard) Cutter Miami on the Grand Banks off Newfoundland Canada. In that test, Fessenden demonstrated depth sounding, underwater communications (Morse code) and echo ranging (detecting an iceberg at two miles (3 km) range). The so-called Fessenden oscillator, at ca. 500 Hz frequency, was unable to determine the bearing of the berg due to the 3 metre wavelength and the small dimension of the transducer's radiating face (less than 1 metre in diameter). The ten Montreal-built British H class submarines launched in 1915 were equipped with a Fessenden oscillator.
During World War I the need to detect submarines prompted more research into the use of sound. The British made early use of underwater listening devices called hydrophones, while the French physicist Paul Langevin, working with a Russian immigrant electrical engineer, Constantin Chilowsky, worked on the development of active sound devices for detecting submarines in 1915. Although piezoelectric and magnetostrictive transducers later superseded the electrostatic transducers they used, this work influenced future designs. Lightweight sound-sensitive plastic film and fibre optics have been used for hydrophones (acousto-electric transducers for in-water use), while Terfenol-D and PMN (lead magnesium niobate) have been developed for projectors.
ASDIC
In 1916, under the British Board of Invention and Research, Canadian physicist Robert William Boyle took on the active sound detection project with A B Wood, producing a prototype for testing in mid-1917. This work, for the Anti-Submarine Division of the British Naval Staff, was undertaken in utmost secrecy, and used quartz piezoelectric crystals to produce the world's first practical underwater active sound detection apparatus. To maintain secrecy no mention of sound experimentation or quartz was made - the word used to describe the early work ('supersonics') was changed to 'ASD'ics, and the quartz material to 'ASD'ivite: "ASD" for "Anti-Submarine Division", hence the British acronym ASDIC. In 1939, in response to a question from the Oxford English Dictionary, the Admiralty made up the story that it stood for 'Allied Submarine Detection Investigation Committee', and this is still widely believed, though no committee bearing this name has been found in the Admiralty archives.
By 1918, both France and Britain had built prototype active systems. The British tested their ASDIC on HMS Antrim in 1920, and started production in 1922. The 6th Destroyer Flotilla had ASDIC-equipped vessels in 1923. An anti-submarine school, HMS Osprey, and a training flotilla of four vessels were established on Portland in 1924. The US Sonar QB set arrived in 1931.
By the outbreak of World War II, the Royal Navy had five sets for different surface ship classes, and others for submarines, incorporated into a complete anti-submarine attack system. The effectiveness of early ASDIC was hamstrung by the use of the depth charge as an anti-submarine weapon. This required an attacking vessel to pass over a submerged contact before dropping charges over the stern, resulting in a loss of ASDIC contact in the moments leading up to attack. The hunter was effectively firing blind, during which time a submarine commander could take evasive action. This situation was remedied by using several ships cooperating and by the adoption of "ahead throwing weapons", such as Hedgehog and later Squid, which projected warheads at a target ahead of the attacker and thus still in ASDIC contact. Developments during the war resulted in British ASDIC sets which used several different shapes of beam, continuously covering blind spots. Later, acoustic torpedoes were used.
At the start of World War II, British ASDIC technology was transferred for free to the United States. Research on ASDIC and underwater sound was expanded in the UK and in the US. Many new types of military sound detection were developed. These included sonobuoys, first developed by the British in 1944 under the codename High Tea, dipping/dunking sonar and mine detection sonar. This work formed the basis for post war developments related to countering the nuclear submarine. Work on sonar had also been carried out in the Axis countries, notably in Germany, which included countermeasures. At the end of World War II this German work was assimilated by Britain and the US. Sonars have continued to be developed by many countries, including Russia, for both military and civil uses. In recent years the major military development has been the increasing interest in low frequency active systems.
SONAR
During the 1930s American engineers developed their own underwater sound detection technology and important discoveries were made, such as thermoclines, that would help future development. After technical information was exchanged between the two countries during the Second World War, Americans began to use the term SONAR for their systems, coined as the equivalent of RADAR.
Materials and designs
There was little progress in development from 1915 to 1940. In 1940, the US sonars typically consisted of a magnetostrictive transducer and an array of nickel tubes connected to a 1-foot-diameter steel plate attached back to back to a Rochelle salt crystal in a spherical housing. This assembly penetrated the ship hull and was manually rotated to the desired angle. The piezoelectric Rochelle salt crystal had better parameters, but the magnetostrictive unit was much more reliable. Early WW2 losses prompted rapid research in the field, pursuing both improvements in magnetostrictive transducer parameters and Rochelle salt reliability. Ammonium dihydrogen phosphate (ADP), a superior alternative, was found as a replacement for Rochelle salt; the first application was a replacement of the 24 kHz Rochelle salt transducers. Within nine months, Rochelle salt was obsolete. The ADP manufacturing facility grew from few dozen personnel in early 1940 to several thousands in 1942.
One of the earliest application of ADP crystals were hydrophones for acoustic mines; the crystals were specified for low frequency cutoff at 5 Hz, withstanding mechanical shock for deployment from aircraft from 3,000 m (10,000 ft), and ability to survive neighbouring mine explosions. One of key features of ADP reliability is its zero aging characteristics; the crystal keeps its parameters even over prolonged storage.
Another application was for acoustic homing torpedoes. Two pairs of directional hydrophones were mounted on the torpedo nose, in the horizontal and vertical plane; the difference signals from the pairs were used to steer the torpedo left-right and up-down. A countermeasure was developed: the targeted submarine discharged an effervescent chemical, and the torpedo went after the noisier fizzy decoy. The counter-countermeasure was a torpedo with active sonar – a transducer was added to the torpedo nose, and the microphones were listening for its reflected periodic tone bursts. The transducers comprised identical rectangular crystal plates arranged to diamond-shaped areas in staggered rows.
Passive sonar arrays for submarines were developed from ADP crystals. Several crystal assemblies were arranged in a steel tube, vacuum-filled with castor oil, and sealed. The tubes then were mounted in parallel arrays.
The standard US Navy scanning sonar at the end of the World War II operated at 18 kHz, using an array of ADP crystals. Desired longer range however required use of lower frequencies. The required dimensions were too big for ADP crystals, so in the early 1950s magnetostrictive and barium titanate piezoelectric systems were developed, but these had problems achieving uniform impedance characteristics and the beam pattern suffered. Barium titanate was then replaced with more stable lead zirconate titanate (PZT), and the frequency was lowered to 5 kHz. The US fleet used this material in the AN/SQS-23 sonar for several decades. The SQS-23 sonar first used magnetostrictive nickel transducers, but these weighed several tons and nickel was expensive and considered a critical material; piezoelectric transducers were therefore substituted. The sonar was a large array of 432 individual transducers. At first the transducers were unreliable, showing mechanical and electrical failures and deteriorating soon after installation; they were also produced by several vendors, had different designs, and their characteristics were different enough to impair the array's performance. The policy to allow repair of individual transducers was then sacrificed, and "expendable modular design", sealed non-repairable modules, was chosen instead, eliminating the problem with seals and other extraneous mechanical parts.
The Imperial Japanese Navy at the onset of WW2 used projectors based on quartz. These were big and heavy, especially if designed for lower frequencies; the one for Type 91 set, operating at 9 kHz, had a diameter of 30 inches and was driven by an oscillator with 5 kW power and 7 kV of output amplitude. The Type 93 projectors consisted of solid sandwiches of quartz, assembled into spherical cast iron bodies. The Type 93 sonars were later replaced with Type 3, which followed German design and used magnetostrictive projectors; the projectors consisted of two rectangular identical independent units in a cast iron rectangular body about 16×9 inches. The exposed area was half the wavelength wide and three wavelengths high. The magnetostrictive cores were made from 4 mm stampings of nickel, and later of an iron-aluminium alloy with aluminium content between 12.7 and 12.9%. The power was provided from a 2 kW at 3.8 kV, with polarization from a 20 V/8 A DC source.
The passive hydrophones of the Imperial Japanese Navy were based on moving coil design, Rochelle salt piezo transducers, and carbon microphones.
Magnetostrictive transducers were pursued after WW2 as an alternative to piezoelectric ones. Nickel scroll-wound ring transducers were used for high-power low-frequency operations, with size up to 13 feet in diameter, probably the largest individual sonar transducers ever. The advantage of metals is their high tensile strength and low input electrical impedance, but they have electrical losses and lower coupling coefficient than PZT, whose tensile strength can be increased by prestressing. Other materials were also tried; nonmetallic ferrites were promising for their low electrical conductivity resulting in low eddy current losses, Metglas offered high coupling coefficient, but they were inferior to PZT overall. In the 1970s, compounds of rare earths and iron were discovered with superior magnetomechanic properties, namely the Terfenol-D alloy. This made possible new designs, e.g. a hybrid magnetostrictive-piezoelectric transducer. The most recent sch material is Galfenol.
Other types of transducers include variable reluctance (or moving armature, or electromagnetic) transducers, where magnetic force acts on the surfaces of gaps, and moving coil (or electrodynamic) transducers, similar to conventional speakers; the latter are used in underwater sound calibration, due to their very low resonance frequencies and flat broadband characteristics above them.
Active sonar
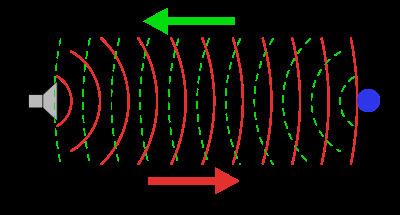
Active sonar uses a sound transmitter and a receiver. When the two are in the same place it is monostatic operation. When the transmitter and receiver are separated it is bistatic operation. When more transmitters (or more receivers) are used, again spatially separated, it is multistatic operation. Most sonars are used monostatically with the same array often being used for transmission and reception. Active sonobuoy fields may be operated multistatically.
Active sonar creates a pulse of sound, often called a "ping", and then listens for reflections (echo) of the pulse. This pulse of sound is generally created electronically using a sonar projector consisting of a signal generator, power amplifier and electro-acoustic transducer/array. A beamformer is usually employed to concentrate the acoustic power into a beam, which may be swept to cover the required search angles. Generally, the electro-acoustic transducers are of the Tonpilz type and their design may be optimised to achieve maximum efficiency over the widest bandwidth, in order to optimise performance of the overall system. Occasionally, the acoustic pulse may be created by other means, e.g. (1) chemically using explosives, or (2) airguns or (3) plasma sound sources.
To measure the distance to an object, the time from transmission of a pulse to reception is measured and converted into a range by knowing the speed of sound. To measure the bearing, several hydrophones are used, and the set measures the relative arrival time to each, or with an array of hydrophones, by measuring the relative amplitude in beams formed through a process called beamforming. Use of an array reduces the spatial response so that to provide wide cover multibeam systems are used. The target signal (if present) together with noise is then passed through various forms of signal processing, which for simple sonars may be just energy measurement. It is then presented to some form of decision device that calls the output either the required signal or noise. This decision device may be an operator with headphones or a display, or in more sophisticated sonars this function may be carried out by software. Further processes may be carried out to classify the target and localise it, as well as measuring its velocity.
The pulse may be at constant frequency or a chirp of changing frequency (to allow pulse compression on reception). Simple sonars generally use the former with a filter wide enough to cover possible Doppler changes due to target movement, while more complex ones generally include the latter technique. Since digital processing became available pulse compression has usually been implemented using digital correlation techniques. Military sonars often have multiple beams to provide all-round cover while simple ones only cover a narrow arc, although the beam may be rotated, relatively slowly, by mechanical scanning.
Particularly when single frequency transmissions are used, the Doppler effect can be used to measure the radial speed of a target. The difference in frequency between the transmitted and received signal is measured and converted into a velocity. Since Doppler shifts can be introduced by either receiver or target motion, allowance has to be made for the radial speed of the searching platform.
One useful small sonar is similar in appearance to a waterproof flashlight. The head is pointed into the water, a button is pressed, and the device displays the distance to the target. Another variant is a "fishfinder" that shows a small display with shoals of fish. Some civilian sonars (which are not designed for stealth) approach active military sonars in capability, with quite exotic three-dimensional displays of the area near the boat.
When active sonar is used to measure the distance from the transducer to the bottom, it is known as echo sounding. Similar methods may be used looking upward for wave measurement.
Active sonar is also used to measure distance through water between two sonar transducers or a combination of a hydrophone (underwater acoustic microphone) and projector (underwater acoustic speaker). A transducer is a device that can transmit and receive acoustic signals ("pings"). When a hydrophone/transducer receives a specific interrogation signal it responds by transmitting a specific reply signal. To measure distance, one transducer/projector transmits an interrogation signal and measures the time between this transmission and the receipt of the other transducer/hydrophone reply. The time difference, scaled by the speed of sound through water and divided by two, is the distance between the two platforms. This technique, when used with multiple transducers/hydrophones/projectors, can calculate the relative positions of static and moving objects in water.
In combat situations, an active pulse can be detected by an opponent and will reveal a submarine's position.
A very directional, but low-efficiency, type of sonar (used by fisheries, military, and for port security) makes use of a complex nonlinear feature of water known as non-linear sonar, the virtual transducer being known as a parametric array.
Project Artemis
Project Artemis was a one-of-a-kind low-frequency sonar for surveillance that was deployed off Bermuda for several years in the early 1960s. The active portion was deployed from a World War II tanker, and the receiving array was a built into a fixed position on an offshore bank.
Transponder
This is an active sonar device that receives a stimulus and immediately (or with a delay) retransmits the received signal or a predetermined one.
Performance prediction
A sonar target is small relative to the sphere, centred around the emitter, on which it is located. Therefore, the power of the reflected signal is very low, several orders of magnitude less than the original signal. Even if the reflected signal was of the same power, the following example (using hypothetical values) shows the problem: Suppose a sonar system is capable of emitting a 10,000 W/m² signal at 1 m, and detecting a 0.001 W/m² signal. At 100 m the signal will be 1 W/m² (due to the inverse-square law). If the entire signal is reflected from a 10 m² target, it will be at 0.001 W/m² when it reaches the emitter, i.e. just detectable. However, the original signal will remain above 0.001 W/m² until 300 m. Any 10 m² target between 100 and 300 m using a similar or better system would be able to detect the pulse but would not be detected by the emitter. The detectors must be very sensitive to pick up the echoes. Since the original signal is much more powerful, it can be detected many times further than twice the range of the sonar (as in the example).
In active sonar there are two performance limitations, due to noise and reverberation. In general one or other of these will dominate so that the two effects can be initially considered separately.
In noise limited conditions at initial detection:
where SL is the source level, TL is the transmission loss (or propagation loss), TS is the target strength, NL is the noise level, DI is the directivity index of the array (an approximation to the array gain) and DT is the detection threshold.
In reverberation limited conditions at initial detection (neglecting array gain):
where RL is the reverberation level and the other factors are as before.
Hand-held sonar for use by a diver
Passive sonar
Passive sonar listens without transmitting. It is often employed in military settings, although it is also used in science applications, e.g., detecting fish for presence/absence studies in various aquatic environments - see also passive acoustics and passive radar. In the very broadest usage, this term can encompass virtually any analytical technique involving remotely generated sound, though it is usually restricted to techniques applied in an aquatic environment.
Identifying sound sources
Passive sonar has a wide variety of techniques for identifying the source of a detected sound. For example, U.S. vessels usually operate 60 Hz alternating current power systems. If transformers or generators are mounted without proper vibration insulation from the hull or become flooded, the 60 Hz sound from the windings can be emitted from the submarine or ship. This can help to identify its nationality, as all European submarines and nearly every other nation's submarine have 50 Hz power systems. Intermittent sound sources (such as a wrench being dropped) may also be detectable to passive sonar. Until fairly recently, an experienced, trained operator identified signals, but now computers may do this.
Passive sonar systems may have large sonic databases, but the sonar operator usually finally classifies the signals manually. A computer system frequently uses these databases to identify classes of ships, actions (i.e. the speed of a ship, or the type of weapon released), and even particular ships. Publications for classification of sounds are provided by and continually updated by the US Office of Naval Intelligence.
Noise limitations
Passive sonar on vehicles is usually severely limited because of noise generated by the vehicle. For this reason, many submarines operate nuclear reactors that can be cooled without pumps, using silent convection, or fuel cells or batteries, which can also run silently. Vehicles' propellers are also designed and precisely machined to emit minimal noise. High-speed propellers often create tiny bubbles in the water, and this cavitation has a distinct sound.
The sonar hydrophones may be towed behind the ship or submarine in order to reduce the effect of noise generated by the watercraft itself. Towed units also combat the thermocline, as the unit may be towed above or below the thermocline.
The display of most passive sonars used to be a two-dimensional waterfall display. The horizontal direction of the display is bearing. The vertical is frequency, or sometimes time. Another display technique is to color-code frequency-time information for bearing. More recent displays are generated by the computers, and mimic radar-type plan position indicator displays.
Performance prediction
Unlike active sonar, only one way propagation is involved. Because of the different signal processing used, the minimum detectable signal to noise ratio will be different. The equation for determining the performance of a passive sonar is:
where SL is the source level, TL is the transmission loss, NL is the noise level, DI is the directivity index of the array (an approximation to the array gain) and DT is the detection threshold. The figure of merit of a passive sonar is:
Performance factors
The detection, classification and localisation performance of a sonar depends on the environment and the receiving equipment, as well as the transmitting equipment in an active sonar or the target radiated noise in a passive sonar.
Sound propagation
Sonar operation is affected by variations in sound speed, particularly in the vertical plane. Sound travels more slowly in fresh water than in sea water, though the difference is small. The speed is determined by the water's bulk modulus and mass density. The bulk modulus is affected by temperature, dissolved impurities (usually salinity), and pressure. The density effect is small. The speed of sound (in feet per second) is approximately:
4388 + (11.25 × temperature (in °F)) + (0.0182 × depth (in feet)) + salinity (in parts-per-thousand ).This empirically derived approximation equation is reasonably accurate for normal temperatures, concentrations of salinity and the range of most ocean depths. Ocean temperature varies with depth, but at between 30 and 100 meters there is often a marked change, called the thermocline, dividing the warmer surface water from the cold, still waters that make up the rest of the ocean. This can frustrate sonar, because a sound originating on one side of the thermocline tends to be bent, or refracted, through the thermocline. The thermocline may be present in shallower coastal waters. However, wave action will often mix the water column and eliminate the thermocline. Water pressure also affects sound propagation: higher pressure increases the sound speed, which causes the sound waves to refract away from the area of higher sound speed. The mathematical model of refraction is called Snell's law.
If the sound source is deep and the conditions are right, propagation may occur in the 'deep sound channel'. This provides extremely low propagation loss to a receiver in the channel. This is because of sound trapping in the channel with no losses at the boundaries. Similar propagation can occur in the 'surface duct' under suitable conditions. However, in this case there are reflection losses at the surface.
In shallow water propagation is generally by repeated reflection at the surface and bottom, where considerable losses can occur.
Sound propagation is affected by absorption in the water itself as well as at the surface and bottom. This absorption depends upon frequency, with several different mechanisms in sea water. Long-range sonar uses low frequencies to minimise absorption effects.
The sea contains many sources of noise that interfere with the desired target echo or signature. The main noise sources are waves and shipping. The motion of the receiver through the water can also cause speed-dependent low frequency noise.
Scattering
When active sonar is used, scattering occurs from small objects in the sea as well as from the bottom and surface. This can be a major source of interference. This acoustic scattering is analogous to the scattering of the light from a car's headlights in fog: a high-intensity pencil beam will penetrate the fog to some extent, but broader-beam headlights emit much light in unwanted directions, much of which is scattered back to the observer, overwhelming that reflected from the target ("white-out"). For analogous reasons active sonar needs to transmit in a narrow beam to minimise scattering.
Target characteristics
The sound reflection characteristics of the target of an active sonar, such as a submarine, are known as its target strength. A complication is that echoes are also obtained from other objects in the sea such as whales, wakes, schools of fish and rocks.
Passive sonar detects the target's radiated noise characteristics. The radiated spectrum comprises a continuous spectrum of noise with peaks at certain frequencies which can be used for classification.
Countermeasures
Active (powered) countermeasures may be launched by a submarine under attack to raise the noise level, provide a large false target, and obscure the signature of the submarine itself.
Passive (i.e., non-powered) countermeasures include:
Military applications
Modern naval warfare makes extensive use of both passive and active sonar from water-borne vessels, aircraft and fixed installations. Although active sonar was used by surface craft in World War II, submarines avoided the use of active sonar due to the potential for revealing their presence and position to enemy forces. However, the advent of modern signal-processing enabled the use of passive sonar as a primary means for search and detection operations. In 1987 a division of Japanese company Toshiba reportedly sold machinery to the Soviet Union that allowed their submarine propeller blades to be milled so that they became radically quieter, making the newer generation of submarines more difficult to detect.
The use of active sonar by a submarine to determine bearing is extremely rare and will not necessarily give high quality bearing or range information to the submarines fire control team. However, use of active sonar on surface ships is very common and is used by submarines when the tactical situation dictates it is more important to determine the position of a hostile submarine than conceal their own position. With surface ships, it might be assumed that the threat is already tracking the ship with satellite data as any vessel around the emitting sonar will detect the emission. Having heard the signal, it is easy to identify the sonar equipment used (usually with its frequency) and its position (with the sound wave's energy). Active sonar is similar to radar in that, while it allows detection of targets at a certain range, it also enables the emitter to be detected at a far greater range, which is undesirable.
Since active sonar reveals the presence and position of the operator, and does not allow exact classification of targets, it is used by fast (planes, helicopters) and by noisy platforms (most surface ships) but rarely by submarines. When active sonar is used by surface ships or submarines, it is typically activated very briefly at intermittent periods to minimize the risk of detection. Consequently, active sonar is normally considered a backup to passive sonar. In aircraft, active sonar is used in the form of disposable sonobuoys that are dropped in the aircraft's patrol area or in the vicinity of possible enemy sonar contacts.
Passive sonar has several advantages, most importantly that it is silent. If the target radiated noise level is high enough, it can have a greater range than active sonar, and allows the target to be identified. Since any motorized object makes some noise, it may in principle be detected, depending on the level of noise emitted and the ambient noise level in the area, as well as the technology used. To simplify, passive sonar "sees" around the ship using it. On a submarine, nose-mounted passive sonar detects in directions of about 270°, centered on the ship's alignment, the hull-mounted array of about 160° on each side, and the towed array of a full 360°. The invisible areas are due to the ship's own interference. Once a signal is detected in a certain direction (which means that something makes sound in that direction, this is called broadband detection) it is possible to zoom in and analyze the signal received (narrowband analysis). This is generally done using a Fourier transform to show the different frequencies making up the sound. Since every engine makes a specific sound, it is straightforward to identify the object. Databases of unique engine sounds are part of what is known as acoustic intelligence or ACINT.
Another use of passive sonar is to determine the target's trajectory. This process is called Target Motion Analysis (TMA), and the resultant "solution" is the target's range, course, and speed. TMA is done by marking from which direction the sound comes at different times, and comparing the motion with that of the operator's own ship. Changes in relative motion are analyzed using standard geometrical techniques along with some assumptions about limiting cases.
Passive sonar is stealthy and very useful. However, it requires high-tech electronic components and is costly. It is generally deployed on expensive ships in the form of arrays to enhance detection. Surface ships use it to good effect; it is even better used by submarines, and it is also used by airplanes and helicopters, mostly to a "surprise effect", since submarines can hide under thermal layers. If a submarine's commander believes he is alone, he may bring his boat closer to the surface and be easier to detect, or go deeper and faster, and thus make more sound.
Examples of sonar applications in military use are given below. Many of the civil uses given in the following section may also be applicable to naval use.
Anti-submarine warfare
Until recently, ship sonars were usually with hull mounted arrays, either amidships or at the bow. It was soon found after their initial use that a means of reducing flow noise was required. The first were made of canvas on a framework, then steel ones were used. Now domes are usually made of reinforced plastic or pressurized rubber. Such sonars are primarily active in operation. An example of a conventional hull mounted sonar is the SQS-56.
Because of the problems of ship noise, towed sonars are also used. These also have the advantage of being able to be placed deeper in the water. However, there are limitations on their use in shallow water. These are called towed arrays (linear) or variable depth sonars (VDS) with 2/3D arrays. A problem is that the winches required to deploy/recover these are large and expensive. VDS sets are primarily active in operation while towed arrays are passive.
An example of a modern active/passive ship towed sonar is Sonar 2087 made by Thales Underwater Systems.
Torpedoes
Modern torpedoes are generally fitted with an active/passive sonar. This may be used to home directly on the target, but wake following torpedoes are also used. An early example of an acoustic homer was the Mark 37 torpedo.
Torpedo countermeasures can be towed or free. An early example was the German Sieglinde device while the Bold was a chemical device. A widely used US device was the towed AN/SLQ-25 Nixie while Mobile submarine simulator (MOSS) was a free device. A modern alternative to the Nixie system is the UK Royal Navy S2170 Surface Ship Torpedo Defence system.
Mines
Mines may be fitted with a sonar to detect, localize and recognize the required target. Further information is given in acoustic mine and an example is the CAPTOR mine.
Mine countermeasures
Mine Countermeasure (MCM) Sonar, sometimes called "Mine and Obstacle Avoidance Sonar (MOAS)", is a specialized type of sonar used for detecting small objects. Most MCM sonars are hull mounted but a few types are VDS design. An example of a hull mounted MCM sonar is the Type 2193 while the SQQ-32 Mine-hunting sonar and Type 2093 systems are VDS designs. See also Minesweeper (ship)
Submarine navigation
Submarines rely on sonar to a greater extent than surface ships as they cannot use radar at depth. The sonar arrays may be hull mounted or towed. Information fitted on typical fits is given in Oyashio class submarine and Swiftsure class submarine.
Aircraft
Helicopters can be used for antisubmarine warfare by deploying fields of active/passive sonobuoys or can operate dipping sonar, such as the AQS-13. Fixed wing aircraft can also deploy sonobuoys and have greater endurance and capacity to deploy them. Processing from the sonobuoys or Dipping Sonar can be on the aircraft or on ship. Dipping sonar has the advantage of being deployable to depths appropriate to daily conditions Helicopters have also been used for mine countermeasure missions using towed sonars such as the AQS-20A.
Underwater communications
Dedicated sonars can be fitted to ships and submarines for underwater communication. See also the section on the underwater acoustics page.
Ocean surveillance
For many years, the United States operated a large set of passive sonar arrays at various points in the world's oceans, collectively called Sound Surveillance System (SOSUS) and later Integrated Undersea Surveillance System (IUSS). A similar system is believed to have been operated by the Soviet Union. As permanently mounted arrays in the deep ocean were utilised, they were in very quiet conditions so long ranges could be achieved. Signal processing was carried out using powerful computers ashore. With the ending of the Cold War a SOSUS array has been turned over to scientific use.
In the United States Navy, a special badge known as the Integrated Undersea Surveillance System Badge is awarded to those who have been trained and qualified in its operation.
Underwater security
Sonar can be used to detect frogmen and other scuba divers. This can be applicable around ships or at entrances to ports. Active sonar can also be used as a deterrent and/or disablement mechanism. One such device is the Cerberus system.
See Underwater Port Security System and Anti-frogman techniques#Ultrasound detection.
Hand-held sonar
Limpet Mine Imaging Sonar (LIMIS) is a hand-held or ROV-mounted imaging sonar designed for patrol divers (combat frogmen or clearance divers) to look for limpet mines in low visibility water.
The LUIS is another imaging sonar for use by a diver.
Integrated Navigation Sonar System (INSS) is a small flashlight-shaped handheld sonar for divers that displays range.
Intercept sonar
This is a sonar designed to detect and locate the transmissions from hostile active sonars. An example of this is the Type 2082 fitted on the British Vanguard class submarines.
Fisheries
Fishing is an important industry that is seeing growing demand, but world catch tonnage is falling as a result of serious resource problems. The industry faces a future of continuing worldwide consolidation until a point of sustainability can be reached. However, the consolidation of the fishing fleets are driving increased demands for sophisticated fish finding electronics such as sensors, sounders and sonars. Historically, fishermen have used many different techniques to find and harvest fish. However, acoustic technology has been one of the most important driving forces behind the development of the modern commercial fisheries.
Sound waves travel differently through fish than through water because a fish's air-filled swim bladder has a different density than seawater. This density difference allows the detection of schools of fish by using reflected sound. Acoustic technology is especially well suited for underwater applications since sound travels farther and faster underwater than in air. Today, commercial fishing vessels rely almost completely on acoustic sonar and sounders to detect fish. Fishermen also use active sonar and echo sounder technology to determine water depth, bottom contour, and bottom composition.
Companies such as eSonar, Raymarine UK, Marport Canada, Wesmar, Furuno, Krupp, and Simrad make a variety of sonar and acoustic instruments for the deep sea commercial fishing industry. For example, net sensors take various underwater measurements and transmit the information back to a receiver on board a vessel. Each sensor is equipped with one or more acoustic transducers depending on its specific function. Data is transmitted from the sensors using wireless acoustic telemetry and is received by a hull mounted hydrophone. The analog signals are decoded and converted by a digital acoustic receiver into data which is transmitted to a bridge computer for graphical display on a high resolution monitor.
Echo sounding
Echo sounding is a process used to determine the depth of water beneath ships and boats. A type of active sonar, echo sounding is the transmission of an acoustic pulse directly downwards to the seabed, measuring the time between transmission and echo return, after having hit the bottom and bouncing back to its ship of origin. The acoustic pulse is emitted by a transducer which receives the return echo as well. The depth measurement is calculated by multiplying the speed of sound in water(averaging 1,500 meters per second) by the time between emission and echo return.
The value of underwater acoustics to the fishing industry has led to the development of other acoustic instruments that operate in a similar fashion to echo-sounders but, because their function is slightly different from the initial model of the echo-sounder, have been given different terms.
Net location
The net sounder is an echo sounder with a transducer mounted on the headline of the net rather than on the bottom of the vessel. Nevertheless, to accommodate the distance from the transducer to the display unit, which is much greater than in a normal echo-sounder, several refinements have to be made. Two main types are available. The first is the cable type in which the signals are sent along a cable. In this case there has to be the provision of a cable drum on which to haul, shoot and stow the cable during the different phases of the operation. The second type is the cable less net-sounder – such as Marport’s Trawl Explorer - in which the signals are sent acoustically between the net and hull mounted receiver/hydrophone on the vessel. In this case no cable drum is required but sophisticated electronics are needed at the transducer and receiver.
The display on a net sounder shows the distance of the net from the bottom (or the surface), rather than the depth of water as with the echo-sounder's hull-mounted transducer. Fixed to the headline of the net, the footrope can usually be seen which gives an indication of the net performance. Any fish passing into the net can also be seen, allowing fine adjustments to be made to catch the most fish possible. In other fisheries, where the amount of fish in the net is important, catch sensor transducers are mounted at various positions on the cod-end of the net. As the cod-end fills up these catch sensor transducers are triggered one by one and this information is transmitted acoustically to display monitors on the bridge of the vessel. The skipper can then decide when to haul the net.
Modern versions of the net sounder, using multiple element transducers, function more like a sonar than an echo sounder and show slices of the area in front of the net and not merely the vertical view that the initial net sounders used.
The sonar is an echo-sounder with a directional capability that can show fish or other objects around the vessel.
ROV and UUV
Small sonars have been fitted to Remotely Operated Vehicles (ROV) and Unmanned Underwater Vehicles (UUV) to allow their operation in murky conditions. These sonars are used for looking ahead of the vehicle. The Long-Term Mine Reconnaissance System is an UUV for MCM purposes.
Vehicle location
Sonars which act as beacons are fitted to aircraft to allow their location in the event of a crash in the sea. Short and Long Baseline sonars may be used for caring out the location, such as LBL.
Prosthesis for the visually impaired
In 2013 an inventor in the United States unveiled a "spider-sense" bodysuit, equipped with ultrasonic sensors and haptic feedback systems, which alerts the wearer of incoming threats; allowing them to respond to attackers even when blindfolded.
Biomass estimation
Detection of fish, and other marine and aquatic life, and estimation their individual sizes or total biomass using active sonar techniques. As the sound pulse travels through water it encounters objects that are of different density or acoustic characteristics than the surrounding medium, such as fish, that reflect sound back toward the sound source. These echoes provide information on fish size, location, abundance and behavior. Data is usually processed and analysed using a variety of software such as Echoview. See Also: Hydroacoustics and Fisheries Acoustics.
Wave measurement
An upward looking echo sounder mounted on the bottom or on a platform may be used to make measurements of wave height and period. From this statistics of the surface conditions at a location can be derived.
Water velocity measurement
Special short range sonars have been developed to allow measurements of water velocity.
Bottom type assessment
Sonars have been developed that can be used to characterise the sea bottom into, for example, mud, sand, and gravel. Relatively simple sonars such as echo sounders can be promoted to seafloor classification systems via add-on modules, converting echo parameters into sediment type. Different algorithms exist, but they are all based on changes in the energy or shape of the reflected sounder pings. Advanced substrate classification analysis can be achieved using calibrated (scientific) echosounders and parametric or fuzzy-logic analysis of the acoustic data (See: Acoustic Seabed Classification)
Bathymetric mapping
Side-scan sonars can be used to derive maps of seafloor topography (bathymetry) by moving the sonar across it just above the bottom. Low frequency sonars such as GLORIA have been used for continental shelf wide surveys while high frequency sonars are used for more detailed surveys of smaller areas.
Sub-bottom profiling
Powerful low frequency echo-sounders have been developed for providing profiles of the upper layers of the ocean bottom.
Synthetic aperture sonar
Various synthetic aperture sonars have been built in the laboratory and some have entered use in mine-hunting and search systems. An explanation of their operation is given in synthetic aperture sonar.
Parametric sonar
Parametric sources use the non-linearity of water to generate the difference frequency between two high frequencies. A virtual end-fire array is formed. Such a projector has advantages of broad bandwidth, narrow beamwidth, and when fully developed and carefully measured it has no obvious sidelobes: see Parametric array. Its major disadvantage is very low efficiency of only a few percent. P.J. Westervelt's seminal 1963 JASA paper summarizes the trends involved.
Sonar in extraterrestrial contexts
Use of sonar has been proposed for determining the depth of hydrocarbon seas on Titan.
Effect on marine mammals
Research has shown that use of active sonar can lead to mass strandings of marine mammals. Beaked whales, the most common casualty of the strandings, have been shown to be highly sensitive to mid-frequency active sonar. Other marine mammals such as the blue whale also flee away from the source of the sonar, while naval activity was suggested to be the most probable cause of a mass stranding of dolphins. The US Navy, which part-funded some of studies, said the findings only showed behavioural responses to sonar, not actual harm, but "will evaluate the effectiveness of [their] marine mammal protective measures in light of new research findings."
Some marine animals, such as whales and dolphins, use echolocation systems, sometimes called biosonar to locate predators and prey. Research on the effects of sonar on blue whales in the Southern California Bight shows that mid-frequency sonar use disrupts the whales' feeding behavior. This indicates that sonar-induced disruption of feeding and displacement from high-quality prey patches could have significant and previously undocumented impacts on baleen whale foraging ecology, individual fitness and population health.
Effect on fish
High intensity sonar sounds can create a small temporary shift in the hearing threshold of some fish.
Frequencies and resolutions
The frequencies of sonars range from infrasonic to above a megahertz. Generally, the lower frequencies have longer range, while the higher frequencies offer better resolution, and smaller size for a given directionality.
To achieve reasonable directionality, frequencies below 1 kHz generally require large size, usually achieved as towed arrays.
Low frequency sonars are loosely defined as 1–5 kHz, albeit some navies regard 5–7 kHz also as low frequency. Medium frequency is defined as 5–15 kHz. Another style of division considers low frequency to be under 1 kHz, and medium frequency at between 1–10 kHz.
American World War II era sonars operated at a relatively high frequency of 20–30 kHz, to achieve directionality with reasonably small transducers, with typical maximum operational range of 2500 yd. Postwar sonars used lower frequencies to achieve longer range; e.g. SQS-4 operated at 10 kHz with range up to 5000 yd. SQS-26 and SQS-53 operated at 3 kHz with range up to 20,000 yd; their domes had size of approx. a 60-ft personnel boat, an upper size limit for conventional hull sonars. Achieving larger sizes by conformal sonar array spread over the hull has not been effective so far, for lower frequencies linear or towed arrays are therefore used.
Japanese WW2 sonars operated at a range of frequencies. The Type 91, with 30 inch quartz projector, worked at 9 kHz. The Type 93, with smaller quartz projectors, operated at 17.5 kHz (model 5 at 16 or 19 kHz magnetostrictive) at powers between 1.7 and 2.5 kilowatts, with range of up to 6 km. The later Type 3, with German-design magnetostrictive transducers, operated at 13, 14.5, 16, or 20 kHz (by model), using twin transducers (except model 1 which had three single ones), at 0.2 to 2.5 kilowatts. The Simple type used 14.5 kHz magnetostrictive transducers at 0.25 kW, driven by capacitive discharge instead of oscillators, with range up to 2.5 km.
The sonar's resolution is angular; objects further apart will be imaged with lower resolutions than nearby ones.
Another source lists ranges and resolutions vs frequencies for sidescan sonars. 30 kHz provides low resolution with range of 1000–6000 m, 100 kHz gives medium resolution at 500–1000 m, 300 kHz gives high resolution at 150–500 m, and 600 kHz gives high resolution at 75–150 m. Longer range sonars are more adversely affected by nonhomogenities of water. Some environments, typically shallow waters near the coasts, have complicated terrain with many features; higher frequencies become necessary there.
As a specific example, the Sonar 2094 Digital, a towed fish capable of reaching depth of 1000 or 2000 meters, performs side-scanning at 114 kHz (600m range at each side, 50 by 1 degree beamwidth) and 410 kHz (150m range, 40 by 0.3 degree beamwidth), with 3 kW pulse power.
A JW Fishers system offers side-scanning at 1200 kHz with very high spatial resolution, optionally coupled with longer-range 600 kHz (range 200 ft at each side) or 100 kHz (up to 2000 ft per side, suitable for scanning large areas for big targets).
