Trajectory

Physics of trajectories

A familiar example of a trajectory is the path of a projectile, such as a thrown ball or rock. In a significantly simplified model, the object moves only under the influence of a uniform gravitational force field. This can be a good approximation for a rock that is thrown for short distances, for example at the surface of the moon. In this simple approximation, the trajectory takes the shape of a parabola. Generally when determining trajectories, it may be necessary to account for nonuniform gravitational forces and air resistance (drag and aerodynamics). This is the focus of the discipline of ballistics.

One of the remarkable achievements of Newtonian mechanics was the derivation of the laws of Kepler. In the gravitational field of a point mass or a spherically-symmetrical extended mass (such as the Sun), the trajectory of a moving object is a conic section, usually an ellipse or a hyperbola. This agrees with the observed orbits of planets, comets, and artificial spacecraft to a reasonably good approximation, although if a comet passes close to the Sun, then it is also influenced by other forces such as the solar wind and radiation pressure, which modify the orbit and cause the comet to eject material into space.

Newton's theory later developed into the branch of theoretical physics known as classical mechanics. It employs the mathematics of differential calculus (which was also initiated by Newton in his youth). Over the centuries, countless scientists have contributed to the development of these two disciplines. Classical mechanics became a most prominent demonstration of the power of rational thought, i.e. reason, in science as well as technology. It helps to understand and predict an enormous range of phenomena; trajectories are but one example.

Consider a particle of mass m , moving in a potential field V . Physically speaking, mass represents inertia, and the field V represents external forces of a particular kind known as "conservative". Given V at every relevant position, there is a way to infer the associated force that would act at that position, say from gravity. Not all forces can be expressed in this way, however.

The motion of the particle is described by the second-order differential equation

m d 2 x → ( t ) d t 2 = − ∇ V ( x → ( t ) )  with  x → = ( x , y , z ) .

On the right-hand side, the force is given in terms of ∇ V , the gradient of the potential, taken at positions along the trajectory. This is the mathematical form of Newton's second law of motion: force equals mass times acceleration, for such situations.

Uniform gravity, neither drag nor wind

The ideal case of motion of a projectile in a uniform gravitational field in the absence of other forces (such as air drag) was first investigated by Galileo Galilei. To neglect the action of the atmosphere in shaping a trajectory would have been considered a futile hypothesis by practical-minded investigators all through the Middle Ages in Europe. Nevertheless, by anticipating the existence of the vacuum, later to be demonstrated on Earth by his collaborator Evangelista Torricelli, Galileo was able to initiate the future science of mechanics. In a near vacuum, as it turns out for instance on the Moon, his simplified parabolic trajectory proves essentially correct.

In the analysis that follows, we derive the equation of motion of a projectile as measured from an inertial frame at rest with respect to the ground. Associated with the frame is a right-hand coordinate system with its origin at the point of launch of the projectile. The x -axis is parallel to the ground, and the y axis is perpendicular to it ( parallel to the gravitational field lines ). Let g be the acceleration of gravity. Relative to the flat terrain, let the initial horizontal speed be v h = v cos ⁡ ( θ ) and the initial vertical speed be v v = v sin ⁡ ( θ ) . It will also be shown that the range is 2 v h v v / g , and the maximum altitude is v v 2 / 2 g . The maximum range for a given initial speed v is obtained when v h = v v , i.e. the initial angle is 45 ∘ . This range is v 2 / g , and the maximum altitude at the maximum range is v 2 / ( 4 g ) .

Derivation of the equation of motion

Assume the motion of the projectile is being measured from a free fall frame which happens to be at (x,y) = (0,0) at t = 0. The equation of motion of the projectile in this frame (by the principle of equivalence) would be y = x tan ⁡ ( θ ) . The co-ordinates of this free-fall frame, with respect to our inertial frame would be y = − g t 2 / 2 . That is, y = − g ( x / v h ) 2 / 2 .

Now translating back to the inertial frame the co-ordinates of the projectile becomes y = x tan ⁡ ( θ ) − g ( x / v h ) 2 / 2 That is:

y = − g sec 2 ⁡ θ 2 v 0 2 x 2 + x tan ⁡ θ ,

(where v₀ is the initial velocity, θ is the angle of elevation, and g is the acceleration due to gravity).

Range and height

The range, R, is the greatest distance the object travels along the x-axis in the I sector. The initial velocity, v_i, is the speed at which said object is launched from the point of origin. The initial angle, θ_i, is the angle at which said object is released. The g is the respective gravitational pull on the object within a null-medium.

R = v i 2 sin ⁡ 2 θ i g

The height, h, is the greatest parabolic height said object reaches within its trajectory

h = v i 2 sin 2 ⁡ θ i 2 g

Angle of elevation

In terms of angle of elevation θ and initial speed v :

v h = v cos ⁡ θ , v v = v sin ⁡ θ

giving the range as

R = 2 v 2 cos ⁡ ( θ ) sin ⁡ ( θ ) / g = v 2 sin ⁡ ( 2 θ ) / g .

This equation can be rearranged to find the angle for a required range

θ = 1 2 sin − 1 ⁡ ( g R v 2 ) (Equation II: angle of projectile launch)

Note that the sine function is such that there are two solutions for θ for a given range d h . The angle θ giving the maximum range can be found by considering the derivative or R with respect to θ and setting it to zero.

d R d θ = 2 v 2 g cos ⁡ ( 2 θ ) = 0

which has a nontrivial solution at 2 θ = π / 2 = 90 ∘ , or θ = 45 ∘ . The maximum range is then R max = v 2 / g . At this angle sin ⁡ ( π / 2 ) = 1 , so the maximum height obtained is v 2 4 g .

To find the angle giving the maximum height for a given speed calculate the derivative of the maximum height H = v 2 sin 2 ⁡ ( θ ) / ( 2 g ) with respect to θ , that is d H d θ = v 2 2 cos ⁡ ( θ ) sin ⁡ ( θ ) / ( 2 g ) which is zero when θ = π / 2 = 90 ∘ . So the maximum height H m a x = v 2 2 g is obtained when the projectile is fired straight up.

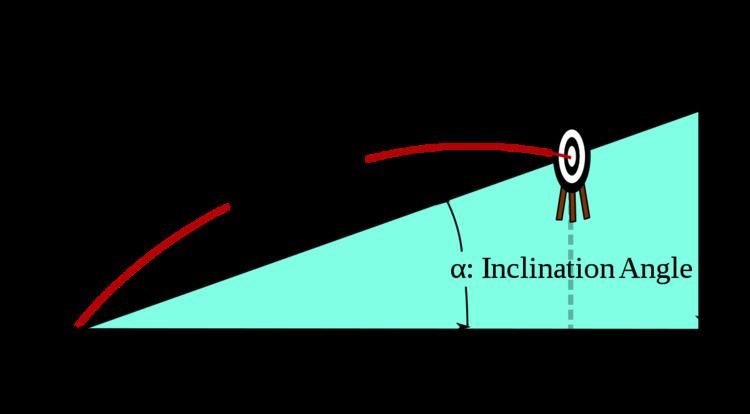
Uphill/downhill in uniform gravity in a vacuum

Given a hill angle α and launch angle θ as before, it can be shown that the range along the hill R s forms a ratio with the original range R along the imaginary horizontal, such that:

R s R = ( 1 − cot ⁡ θ tan ⁡ α ) sec ⁡ α (Equation 11)

In this equation, downhill occurs when α is between 0 and -90 degrees. For this range of α we know: tan ⁡ ( − α ) = − tan ⁡ α and sec ⁡ ( − α ) = sec ⁡ α . Thus for this range of α , R s / R = ( 1 + tan ⁡ θ tan ⁡ α ) sec ⁡ α . Thus R s / R is a positive value meaning the range downhill is always further than along level terrain. The lower level of terrain causes the projectile to remain in the air longer, allowing it to travel further horizontally before hitting the ground.

While the same equation applies to projectiles fired uphill, the interpretation is more complex as sometimes the uphill range may be shorter or longer than the equivalent range along level terrain. Equation 11 may be set to R s / R = 1 (i.e. the slant range is equal to the level terrain range) and solving for the "critical angle" θ cr :

1 = ( 1 − tan ⁡ θ tan ⁡ α ) sec ⁡ α θ cr = arctan ⁡ ( ( 1 − csc ⁡ α ) cot ⁡ α )

Equation 11 may also be used to develop the "rifleman's rule" for small values of α and θ (i.e. close to horizontal firing, which is the case for many firearm situations). For small values, both tan ⁡ α and tan ⁡ θ have a small value and thus when multiplied together (as in equation 11), the result is almost zero. Thus equation 11 may be approximated as:

R s R = ( 1 − 0 ) sec ⁡ α

And solving for level terrain range, R

R = R s cos ⁡ α   "Rifleman's rule"

Thus if the shooter attempts to hit the level distance R, s/he will actually hit the slant target. "In other words, pretend that the inclined target is at a horizontal distance equal to the slant range distance multiplied by the cosine of the inclination angle, and aim as if the target were really at that horizontal position."[1]

Derivation based on equations of a parabola

The intersect of the projectile trajectory with a hill may most easily be derived using the trajectory in parabolic form in Cartesian coordinates (Equation 10) intersecting the hill of slope m in standard linear form at coordinates ( x , y ) :

y = m x + b (Equation 12) where in this case, y = d v , x = d h and b = 0

Substituting the value of d v = m d h into Equation 10:

m x = − g 2 v 2 cos 2 ⁡ θ x 2 + sin ⁡ θ cos ⁡ θ x x = 2 v 2 cos 2 ⁡ θ g ( sin ⁡ θ cos ⁡ θ − m ) (Solving above for x)

This value of x may be substituted back into the linear equation 12 to get the corresponding y coordinate at the intercept:

y = m x = m 2 v 2 cos 2 ⁡ θ g ( sin ⁡ θ cos ⁡ θ − m )

Now the slant range R s is the distance of the intercept from the origin, which is just the hypotenuse of x and y:

R s = x 2 + y 2 = ( 2 v 2 cos 2 ⁡ θ g ( sin ⁡ θ cos ⁡ θ − m ) ) 2 + ( m 2 v 2 cos 2 ⁡ θ g ( sin ⁡ θ cos ⁡ θ − m ) ) 2 = 2 v 2 cos 2 ⁡ θ g ( sin ⁡ θ cos ⁡ θ − m ) 2 + m 2 ( sin ⁡ θ cos ⁡ θ − m ) 2 = 2 v 2 cos 2 ⁡ θ g ( sin ⁡ θ cos ⁡ θ − m ) 1 + m 2

Now α is defined as the angle of the hill, so by definition of tangent, m = tan ⁡ α . This can be substituted into the equation for R s :

R s = 2 v 2 cos 2 ⁡ θ g ( sin ⁡ θ cos ⁡ θ − tan ⁡ α ) 1 + tan 2 ⁡ α

Now this can be refactored and the trigonometric identity for sec ⁡ α = 1 + tan 2 ⁡ α may be used:

R s = 2 v 2 cos ⁡ θ sin ⁡ θ g ( 1 − cos ⁡ θ sin ⁡ θ tan ⁡ α ) sec ⁡ α

Now the flat range R = v 2 sin ⁡ 2 θ / g = 2 v 2 sin ⁡ θ cos ⁡ θ / g by the previously used trigonometric identity and cos ⁡ θ / sin ⁡ θ = cot ⁡ θ so:

R s = R ( 1 − cot ⁡ θ tan ⁡ α ) sec ⁡ α R s R = ( 1 − cot ⁡ θ tan ⁡ α ) sec ⁡ α

Orbiting objects

If instead of a uniform downwards gravitational force we consider two bodies orbiting with the mutual gravitation between them, we obtain Kepler's laws of planetary motion. The derivation of these was one of the major works of Isaac Newton and provided much of the motivation for the development of differential calculus.

Catching balls

If a projectile, such as a baseball or cricket ball, travels in a parabolic path, with negligible air resistance, and if a player is positioned so as to catch it as it descends, he sees its angle of elevation increasing continuously throughout its flight. The tangent of the angle of elevation is proportional to the time since the ball was sent into the air, usually by being struck with a bat. Even when the ball is really descending, near the end of its flight, its angle of elevation seen by the player continues to increase. The player therefore sees it as if it were ascending vertically at constant speed. Finding the place from which the ball appears to rise steadily helps the player to position himself correctly to make the catch. If he is too close to the batsman who has hit the ball, it will appear to rise at an accelerating rate. If he is too far from the batsman, it will appear to slow rapidly, and then to descend.