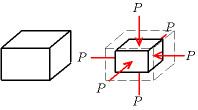
Bulk modulus

Definition

The bulk modulus K > 0 can be formally defined by the equation

where P is pressure, V is volume, and d P / d V denotes the derivative of pressure with respect to volume. Equivalently

where ρ is density and dP/dρ denotes the derivative of pressure with respect to density (i.e. pressure rate of change with volume). The inverse of the bulk modulus gives a substance's compressibility.

Other moduli describe the material's response (strain) to other kinds of stress: the shear modulus describes the response to shear, and Young's modulus describes the response to linear stress. For a fluid, only the bulk modulus is meaningful. For an anisotropic solid such as wood or paper, these three moduli do not contain enough information to describe its behaviour, and one must use the full generalized Hooke's law.

Thermodynamic relation

Strictly speaking, the bulk modulus is a thermodynamic quantity, and in order to specify a bulk modulus it is necessary to specify how the temperature varies during compression: constant-temperature (isothermal K T ), constant-entropy (isentropic K S ), and other variations are possible. Such distinctions are especially relevant for gases.

For an ideal gas, the isentropic bulk modulus K S is given by

and the isothermal bulk modulus K T is given by

where

When the gas is not ideal, these equations give only an approximation of the bulk modulus. In a fluid, the bulk modulus K and the density ρ determine the speed of sound c (pressure waves), according to the Newton-Laplace formula

In solids, K S and K T have very similar values. Solids can also sustain transverse waves: for these materials one additional elastic modulus, for example the shear modulus, is needed to determine wave speeds.

Measurement

It is possible to measure the bulk modulus using powder diffraction under applied pressure. It is a property of a fluid which shows its ability to change its volume under its pressure.

Selected values

A material with a bulk modulus of 35 GPa loses one percent of its volume when subjected to an external pressure of 0.35 GPa (~7008350000000000000♠3500 bar).