 | ||
In number theory, the Mertens function is defined for all positive integers n as
Contents
- As an integral
- As a sum over Farey sequences
- As a determinant
- As a sum of the number of points under n dimensional hyperboloids
- Calculation
- References
where μ(k) is the Möbius function. The function is named in honour of Franz Mertens. This definition can be extended to positive real numbers as follows:
Less formally, M(x) is the count of square-free integers up to x that have an even number of prime factors, minus the count of those that have an odd number.
The first 143 M(n) is: (sequence A002321 in the OEIS)
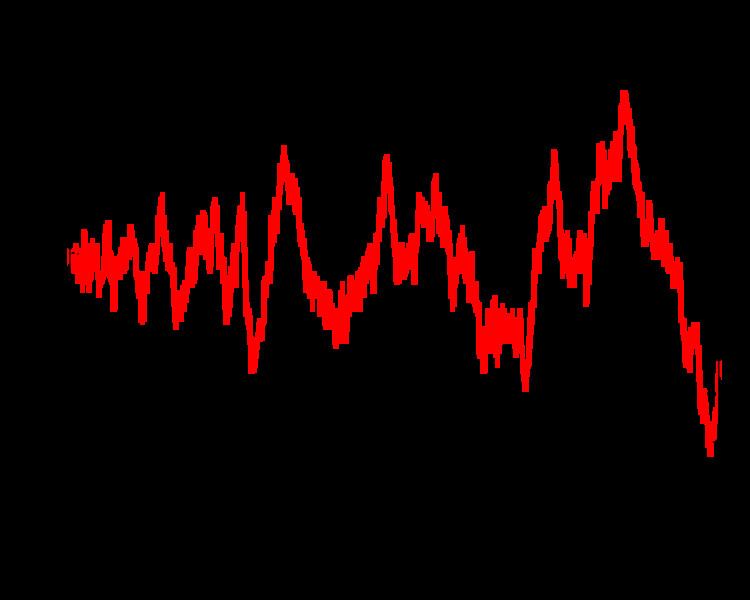
The Mertens function slowly grows in positive and negative directions both on average and in peak value, oscillating in an apparently chaotic manner passing through zero when n has the values
2, 39, 40, 58, 65, 93, 101, 145, 149, 150, 159, 160, 163, 164, 166, 214, 231, 232, 235, 236, 238, 254, 329, 331, 332, 333, 353, 355, 356, 358, 362, 363, 364, 366, 393, 401, 403, 404, 405, 407, 408, 413, 414, 419, 420, 422, 423, 424, 425, 427, 428, ... (sequence A028442 in the OEIS).Because the Möbius function only takes the values −1, 0, and +1, the Mertens function moves slowly and there is no x such that |M(x)| > x. The Mertens conjecture went further, stating that there would be no x where the absolute value of the Mertens function exceeds the square root of x. The Mertens conjecture was proven false in 1985 by Andrew Odlyzko and Herman te Riele. However, the Riemann hypothesis is equivalent to a weaker conjecture on the growth of M(x), namely M(x) = O(x1/2 + ε). Since high values for M(x) grow at least as fast as the square root of x, this puts a rather tight bound on its rate of growth. Here, O refers to Big O notation.
The true rate of growth of M(x) is not known. An unpublished conjecture of Steve Gonek states that
Probabilistic evidence towards this conjecture is given by Nathan Ng.
As an integral
Using the Euler product one finds that
where
where c > 1.
Conversely, one has the Mellin transform
which holds for
A curious relation given by Mertens himself involving the second Chebyshev function is
Assuming that there are not multiple non-trivial roots of
Weyl conjectured that the Mertens function satisfied the approximate functional-differential equation
where H(x) is the Heaviside step function, B are Bernoulli numbers and all derivatives with respect to t are evaluated at t = 0.
There is also a trace formula involving a sum over the Möbius function and zeros of Riemann Zeta in the form
where the first sum on the right-hand side is over the nontrivial zeros of the Riemann zeta function, and (g,h) are related by a Fourier transform, such that
As a sum over Farey sequences
Another formula for the Mertens function is
This formula is used in the proof of the Franel–Landau theorem.
As a determinant
M(n) is the determinant of the n × n Redheffer matrix, a (0,1) matrix in which aij is 1 if either j is 1 or i divides j.
As a sum of the number of points under n-dimensional hyperboloids
Calculation
Neither of the methods mentioned previously leads to practical algorithms to calculate the Mertens function. Using sieve methods similar to those used in prime counting, the Mertens function has been computed for all integers up to an increasing range of x.
The Mertens function for all integer values up to x may be computed in O(x log log x) time. Combinatorial based algorithms can compute isolated values of M(x) in O(x2/3(log log x)1/3) time, and faster non-combinatorial methods are also known.
See A084237 for values of M(x) at powers of 10.
