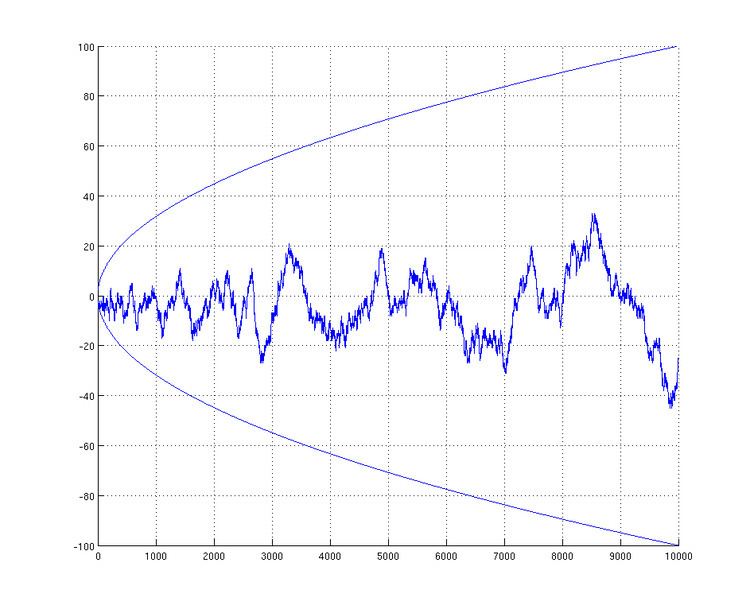
Mertens conjecture - Alchetron, The Free Social Encyclopedia

In mathematics, the Mertens conjecture is the false statement that the Mertens function M(n) is bounded by √n, which implies the Riemann hypothesis. It was conjectured by Thomas Joannes Stieltjes in an 1885 letter to Charles Hermite (reprinted in Stieltjes 1905) and Mertens (1897), and disproved by Odlyzko & te Riele (1985). It is a striking example of a mathematical proof contradicting a large amount of computational evidence in favor of a conjecture.

Definition

In number theory, we define the Mertens function as

M ( n ) = ∑ 1 ≤ k ≤ n μ ( k )

where μ(k) is the Möbius function; the Mertens conjecture is that for all n > 1,

| M ( n ) | < n .

Disproof of the conjecture

Stieltjes claimed in 1885 to have proven a weaker result, namely that m ( n ) = M ( n ) / n was bounded, but did not publish a proof. (In terms of m ( n ) , the Mertens conjecture is that − 1 < m ( n ) < 1 .)

In 1985, Andrew Odlyzko and Herman te Riele conditionally proved the Mertens conjecture false: indeed, lim inf m ( n ) < − 1.009 and lim sup m ( n ) > 1.06 . It was later shown that the first counterexample appears below exp(3.21×10⁶⁴) (~10^{1.39×10⁶⁴}) (Pintz 1987) but above 10¹⁴. The upper bound has since been lowered to exp(1.59×10⁴⁰) (Kotnik and Te Riele 2006), but no counterexample is explicitly known. The boundedness claim made by Stieltjes, while remarked upon as "very unlikely" in the 1985 paper cited above, has not been disproven (as of 2009). The law of the iterated logarithm states that if μ is replaced by a random sequence of +1s and −1s then the order of growth of the partial sum of the first n terms is (with probability 1) about (n log log n)^1/2, which suggests that the order of growth of m(n) might be somewhere around (log log n)^1/2. The actual order of growth may be somewhat smaller; it was conjectured by Steve Gonek in the early 1990s that the order of growth of m(n) was ( log ⁡ log ⁡ log ⁡ n ) 5 / 4 , which was also conjectured by Ng (2004), based on a heuristic argument assuming the Riemann hypothesis and certain conjectures about the averaged behavior of zeros of the Riemann zeta function.

In 1979 Cohen and Dress found the largest known value of m ( n ) ≈ 0.570591 for M(7766842813) = 50286, and in 2011 Kuznetsov found the largest known negative value m ( n ) ≈ − 0.585768 for M(11609864264058592345) = -1995900927. In 2016 Hurst computed M(n) for every n ≤ 10¹⁶ but did not find larger values of m(n).

In 2006, Kotnik and te Riele improved the upper bound and showed that there are infinitely many values of n for which m(n)>1.2184, but without giving any specific value for such an n. In 2016, Hurst made further improvements by showing lim inf m ( n ) < − 1.837625 and lim sup m ( n ) > 1.826054 .

Connection to the Riemann hypothesis

The connection to the Riemann hypothesis is based on the Dirichlet series for the reciprocal of the Riemann zeta function,

1 ζ ( s ) = ∑ n = 1 ∞ μ ( n ) n s ,

valid in the region ℜ ( s ) > 1 . We can rewrite this as a Stieltjes integral

1 ζ ( s ) = ∫ 0 ∞ x − s d M ( x )

and after integrating by parts, obtain the reciprocal of the zeta function as a Mellin transform

1 s ζ ( s ) = { M M } ( − s ) = ∫ 0 ∞ x − s M ( x ) d x x .

Using the Mellin inversion theorem we now can express M in terms of 1/ζ as

M ( x ) = 1 2 π i ∫ σ − i ∞ σ + i ∞ x s s ζ ( s ) d s

which is valid for 1 < σ < 2, and valid for 1/2 < σ < 2 on the Riemann hypothesis. From this, the Mellin transform integral must be convergent, and hence M(x) must be O(x^e) for every exponent e greater than 1/2. From this it follows that

M ( x ) = O ( x 1 2 + ϵ )

for all positive ε is equivalent to the Riemann hypothesis, which therefore would have followed from the stronger Mertens hypothesis, and follows from the hypothesis of Stieltjes that

M ( x ) = O ( x 1 2 ) .

References

Mertens conjecture Wikipedia

(Text) CC BY-SA

Contents

Definition

Disproof of the conjecture

Connection to the Riemann hypothesis

References