Kepler orbit

Introduction

From ancient times until the 16th and 17th centuries, the motions of the planets were believed to follow perfectly circular geocentric paths as taught by the ancient Greek philosophers Aristotle and Ptolemy. Variations in the motions of the planets were explained by smaller circular paths overlaid on the larger path (see epicycle). As measurements of the planets became increasingly accurate, revisions to the theory were proposed. In 1543, Nicolaus Copernicus published a heliocentric model of the solar system, although he still believed that the planets traveled in perfectly circular paths centered on the sun.

Johannes Kepler

In 1601, Johannes Kepler acquired the extensive, meticulous observations of the planets made by Tycho Brahe. Kepler would spend the next five years trying to fit the observations of the planet Mars to various curves. In 1609, Kepler published the first two of his three laws of planetary motion. The first law states:

"The orbit of every planet is an ellipse with the sun at a focus."

More generally, the path of an object undergoing Keplerian motion may also follow a parabola or a hyperbola, which, along with ellipses, belong to a group of curves known as conic sections. Mathematically, the distance between a central body and an orbiting body can be expressed as:

r ( θ ) = a ( 1 − e 2 ) 1 + e cos ⁡ ( θ )

where:

r is the distance

a is the semi-major axis, which defines the size of the orbit

e is the eccentricity, which defines the shape of the orbit

θ is the true anomaly, which is the angle between the current position of the orbiting object and the location in the orbit at which it is closest to the central body (called the periapsis), according to the figure above.

Alternately, the equation can be expressed as:

r ( θ ) = p 1 + e cos ⁡ ( θ )

Where p is called the semi-latus rectum of the curve. This form of the equation is particularly useful when dealing with parabolic trajectories, for which the semi-major axis is infinite.

Despite developing these laws from observations, Kepler was never able to develop a theory to explain these motions.

Isaac Newton

Between 1665 and 1666, Isaac Newton developed several concepts related to motion, gravitation and differential calculus. However, these concepts were not published until 1687 in the Principia, in which he outlined his laws of motion and his law of universal gravitation. His second of his three laws of motion states:

The acceleration a of a body is parallel and directly proportional to the net force acting on the body, is in the direction of the net force, and is inversely proportional to the mass of the body:

F = m a = m d 2 r d t 2

Where:

F is the force vector

m is the mass of the body on which the force is acting

a is the acceleration vector, the second time derivative of the position vector r

Strictly speaking, this form of the equation only applies to an object of constant mass, which holds true based on the simplifying assumptions made below.

Newton's law of gravitation states:

Every point mass attracts every other point mass by a force pointing along the line intersecting both points. The force is proportional to the product of the two masses and inversely proportional to the square of the distance between the point masses:

F = G m 1 m 2 r 2

where:

F is the magnitude of the gravitational force between the two point masses

G is the gravitational constant

m 1 is the mass of the first point mass

m 2 is the mass of the second point mass

r is the distance between the two point masses

From the laws of motion and the law of universal gravitation, Newton was able to derive Kepler's laws, demonstrating consistency between observation and theory. The laws of Kepler and Newton formed the basis of modern celestial mechanics until Albert Einstein introduced the concepts of special and general relativity in the early 20th century. For most applications, Keplerian motion approximates the motions of planets and satellites to relatively high degrees of accuracy and is used extensively in astronomy and astrodynamics.

Simplified two body problem

See also Orbit Analysis

To solve for the motion of an object in a two body system, two simplifying assumptions can be made:

1. The bodies are spherically symmetric and can be treated as point masses.2. There are no external or internal forces acting upon the bodies other than their mutual gravitation.

The shapes of large celestial bodies are close to spheres. By symmetry, the net gravitational force attracting a mass point towards a homogeneous sphere must be directed towards its centre. The shell theorem (also proven by Isaac Newton) states that the magnitude of this force is the same as if all mass was concentrated in the middle of the sphere, even if the density of the sphere varies with depth (as it does for most celestial bodies). From this immediately follows that the attraction between two homogeneous spheres is as if both had its mass concentrated to its center.

Smaller objects, like asteroids or spacecraft often have a shape strongly deviating from a sphere. But the gravitational forces produced by these irregularities are generally small compared to the gravity of the central body. The difference between an irregular shape and a perfect sphere also diminishes with distances, and most orbital distances are very large when compared with the diameter of a small orbiting body. Thus for some applications, shape irregularity can be neglected without significant impact on accuracy.

Planets rotate at varying rates and thus may take a slightly oblate shape because of the centrifugal force. With such an oblate shape, the gravitational attraction will deviate somewhat from that of a homogeneous sphere. This phenomenon is quite noticeable for artificial Earth satellites, especially those in low orbits. At larger distances the effect of this oblateness becomes negligible. Planetary motions in the Solar System can be computed with sufficient precision if they are treated as point masses.

Two point mass objects with masses m 1 and m 2 and position vectors r 1 and r 2 relative to some inertial reference frame experience gravitational forces:

m 1 r ¨ 1 = − G m 1 m 2 r 2 r ^ m 2 r ¨ 2 = G m 1 m 2 r 2 r ^

where r is the relative position vector of mass 1 with respect to mass 2, expressed as:

r = r 1 − r 2

and r ^ is the unit vector in that direction and r is the length of that vector.

Dividing by their respective masses and subtracting the second equation from the first yields the equation of motion for the acceleration of the first object with respect to the second:

where μ is the gravitational parameter and is equal to

μ = G ( m 1 + m 2 )

In many applications, a third simplifying assumption can be made:

3. When compared to the central body, the mass of the orbiting body is insignificant. Mathematically, m₁ >> m₂, so μ = G (m₁ + m₂) ≈ Gm₁.

This assumption is not necessary to solve the simplified two body problem, but it simplifies calculations, particularly with Earth-orbiting satellites and planets orbiting the sun. Even Jupiter's mass is less than the sun's by a factor of 1047, which would constitute an error of 0.096% in the value of μ. Notable exceptions include the Earth-moon system (mass ratio of 81.3), the Pluto-Charon system (mass ratio of 8.9) and binary star systems.

Under these assumptions the differential equation for the two body case can be completely solved mathematically and the resulting orbit which follows Kepler's laws of planetary motion is called a "Kepler orbit". The orbits of all planets are to high accuracy Kepler orbits around the Sun. The small deviations are due to the much weaker gravitational attractions between the planets, and in the case of Mercury, due to general relativity. The orbits of the artificial satellites around the Earth are, with a fair approximation, Kepler orbits with small perturbations due to the gravitational attraction of the sun, the moon and the oblateness of the Earth. In high accuracy applications for which the equation of motion must be integrated numerically with all gravitational and non-gravitational forces (such as solar radiation pressure and atmospheric drag) being taken into account, the Kepler orbit concepts are of paramount importance and heavily used.

Keplerian elements

It is worth mentioning that any Keplerian trajectory can be defined by six parameters. The motion of an object moving in three-dimensional space is characterized by a position vector and a velocity vector. Each vector has three components, so the total number of values needed to define a trajectory through space is six. An orbit is generally defined by six elements (known as Keplerian elements) that can be computed from position and velocity, three of which have already been discussed. These elements are convenient in that of the six, five are unchanging for an unperturbed orbit (a stark contrast to two constantly changing vectors). The future location of an object within its orbit can be predicted and its new position and velocity can be easily obtained from the orbital elements.

Two define the size and shape of the trajectory:

Semimajor axis ( a )

Eccentricity ( e )

Three define the orientation of the orbital plane:

Inclination ( i ) defines the angle between the orbital plane and the reference plane.

Longitude of the ascending node ( Ω ) defines the angle between the reference direction and the upward crossing of the orbit on the reference plane (the ascending node).

Argument of periapsis ( ω ) defines the angle between the ascending node and the periapsis.

And finally:

True anomaly ( ν ) defines the position of the orbiting body along the trajectory, measured from periapsis. Several alternate values can be used instead of true anomaly, the most common being M the mean anomaly and T , the time since periapsis.

Because i , Ω and ω are simply angular measurements defining the orientation of the trajectory in the reference frame, they are not strictly necessary when discussing the motion of the object within the orbital plane. They have been mentioned here for completeness, but are not required for the proofs below.

Mathematical solution of the differential equation (1) above

For movement under any central force, i.e. a force parallel to r, the specific relative angular momentum H = r × r ˙ stays constant:
H ˙ = d d t ( r × r ˙ ) = r ˙ × r ˙ + r × r ¨ = 0 + 0 = 0

Since the cross product of the position vector and its velocity stays constant, they must lie in the same plane, orthogonal to H . This implies the vector function is a plane curve.
Because the equation has symmetry around its origin, it is easier to solve in polar coordinates. However, it is important to note that equation (1) refers to linear acceleration ( r ¨ ) , as opposed to angular ( θ ¨ ) or radial ( r ¨ ) acceleration. Therefore, one must be cautious when transforming the equation. Introducing a cartesian coordinate system ( x ^   ,   y ^ ) and polar unit vectors ( r ^   ,   θ ^ ) in the plane orthogonal to H :

r ^ = cos ⁡ ( θ ) x ^ + sin ⁡ ( θ ) y ^
θ ^ = − sin ⁡ ( θ ) x ^ + cos ⁡ ( θ ) y ^

We can now rewrite the vector function r and its derivatives as:

r = r ( cos ⁡ θ x ^ + sin ⁡ θ y ^ ) = r r ^

r ˙ = r ˙ r ^ + r θ ˙ θ ^

r ¨ = ( r ¨ − r θ ˙ 2 ) r ^ + ( r θ ¨ + 2 r ˙ θ ˙ ) θ ^

(see "Vector calculus"). Substituting these into (1), we find:

( r ¨ − r θ ˙ 2 ) r ^ + ( r θ ¨ + 2 r ˙ θ ˙ ) θ ^ = ( − μ r 2 ) r ^ + ( 0 ) θ ^

This gives the non-ordinary polar differential equation:

In order to solve this equation, we must first eliminate all time derivatives. We find that:

H = | r × r ˙ | = | ( r cos ⁡ ( θ ) , r sin ⁡ ( θ ) , 0 ) × ( r ˙ cos ⁡ ( θ ) − r sin ⁡ ( θ ) θ ˙ , r ˙ sin ⁡ ( θ ) + r cos ⁡ ( θ ) θ ˙ , 0 ) | = | ( 0 , 0 , r 2 θ ˙ ) | = r 2 θ ˙

Taking the time derivative of (3), we get

Equations (3) and (4) allow us to eliminate the time derivatives of θ . In order to eliminate the time derivatives of r , we must use the chain rule to find appropriate substitutions:

Using these four substitutions, all time derivatives in (2) can be eliminated, yielding an ordinary differential equation for r as function of θ .

r ¨ − r θ ˙ 2 = − μ r 2

d 2 r d θ 2 ⋅ θ ˙ 2 + d r d θ ⋅ θ ¨ − r θ ˙ 2 = − μ r 2

d 2 r d θ 2 ⋅ ( H r 2 ) 2 + d r d θ ⋅ ( − 2 ⋅ H ⋅ r ˙ r 3 ) − r ( H r 2 ) 2 = − μ r 2

The differential equation (7) can be solved analytically by the variable substitution

Using the chain rule for differentiation one gets:

Using the expressions (10) and (9) for d 2 r d θ 2 and d r d θ one gets

with the general solution

where e and θ 0 are constants of integration depending on the initial values for s and d s d θ .

Instead of using the constant of integration θ 0 explicitly one introduces the convention that the unit vectors x ^   ,   y ^ defining the coordinate system in the orbital plane are selected such that θ 0 takes the value zero and e is positive. This then means that θ is zero at the point where s is maximal and therefore r = 1 s is minimal. Defining the parameter p as H 2 μ one has that
r = 1 s = p 1 + e ⋅ cos ⁡ θ

Alternate derivation

Another way to solve this equation without the use of polar differential equations is as follows:
Define a unit vector u such that r = r u and r ¨ = − μ r 2 u . It follows that

H = r × r ˙ = r u × d d t ( r u ) = r u × ( r u ˙ + r ˙ u ) = r 2 ( u × u ˙ ) + r r ˙ ( u × u ) = r 2 u × u ˙

Now consider

r ¨ × H = − μ r 2 u × ( r 2 u × u ˙ ) = − μ u × ( u × u ˙ ) = − μ [ ( u ⋅ u ˙ ) u − ( u ⋅ u ) u ˙ ]

(see Vector triple product). Notice that

u ⋅ u = | u | 2 = 1

u ⋅ u ˙ = 1 2 ( u ⋅ u ˙ + u ˙ ⋅ u ) = 1 2 d d t ( u ⋅ u ) = 0

Substituting these values into the previous equation, one gets:

r ¨ × H = μ u ˙

Integrating both sides:

r ˙ × H = μ u + c

Where c is a constant vector. Dotting this with r yields an interesting result:

r ⋅ ( r ˙ × H ) = r ⋅ ( μ u + c ) = μ r ⋅ u + r ⋅ c = μ r ( u ⋅ u ) + r c cos ⁡ ( θ ) = r ( μ + c cos ⁡ ( θ ) )

Where θ is the angle between r and c . Solving for r:

r = r ⋅ ( r ˙ × H ) μ + c cos ⁡ ( θ ) = ( r × r ˙ ) ⋅ H μ + c cos ⁡ ( θ ) = | H | 2 μ + c cos ⁡ ( θ )

Notice that ( r , θ ) are effectively the polar coordinates of the vector function. Making the substitutions p = | H | 2 μ and e = c μ , we again arrive at the equation

This is the equation in polar coordinates for a conic section with origin in a focal point. The argument θ is called "true anomaly".

Properties of trajectory equation

For e   =   0 this is a circle with radius p.

For 0   < e   <   1 this is an ellipse with

For e   =   1 this is a parabola with focal length p 2

For e   >   1 this is a hyperbola with

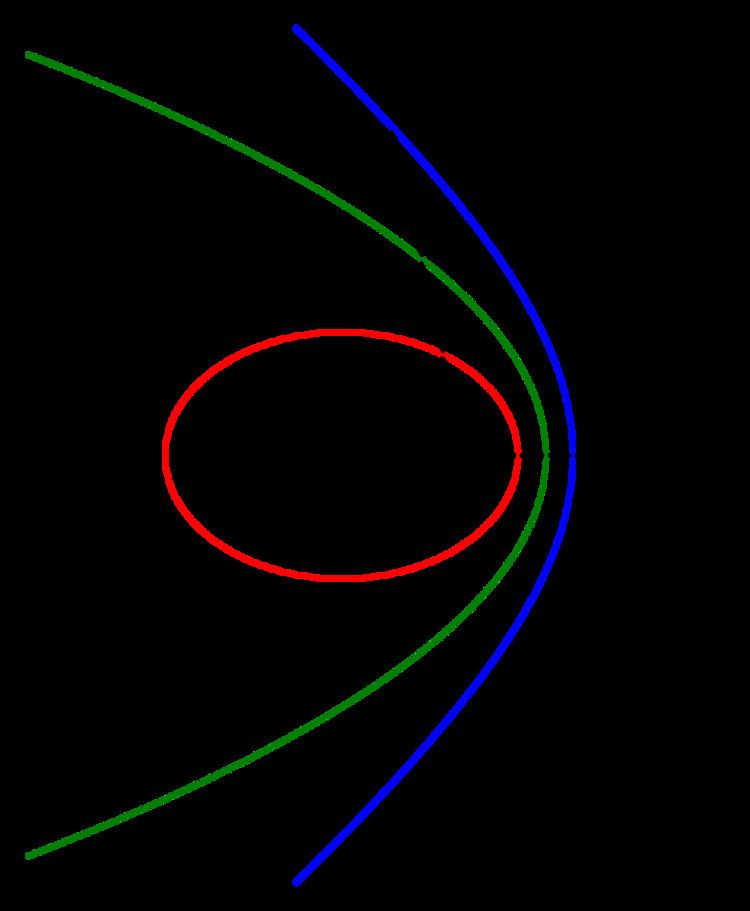
The following image illustrates a circle (grey), an ellipse (red), a parabola (green) and a hyperbola (blue)

The point on the horizontal line going out to the right from the focal point is the point with θ = 0 for which the distance to the focus takes the minimal value p 1 + e , the pericentre. For the ellipse there is also an apocentre for which the distance to the focus takes the maximal value p 1 − e . For the hyperbola the range for θ is

[ − cos − 1 ⁡ ( − 1 e ) < θ < cos − 1 ⁡ ( − 1 e ) ]

and for a parabola the range is

[ − π < θ < π ]

Using the chain rule for differentiation (5), the equation (2) and the definition of p as H 2 μ one gets that the radial velocity component is

and that the tangential component (velocity component perpendicular to V r ) is

The connection between the polar argument θ and time t is slightly different for elliptic and hyperbolic orbits.

For an elliptic orbit one switches to the "eccentric anomaly" E for which

and consequently

and the angular momentum H is

Integrating with respect to time t one gets

under the assumption that time t = 0 is selected such that the integration constant is zero.

As by definition of p one has

this can be written

For a hyperbolic orbit one uses the hyperbolic functions for the parameterisation

for which one has

and the angular momentum H is

Integrating with respect to time t one gets

i.e.

To find what time t that corresponds to a certain true anomaly θ one computes corresponding parameter E connected to time with relation (27) for an elliptic and with relation (34) for a hyperbolic orbit.

Note that the relations (27) and (34) define a mapping between the ranges

[ − ∞ < t < ∞ ] ⟷ [ − ∞ < E < ∞ ]

Some additional formulae

For an elliptic orbit one gets from (20) and (21) that

and therefore that

From (36) then follows that

tan 2 ⁡ θ 2 = 1 − cos ⁡ θ 1 + cos ⁡ θ = 1 − cos ⁡ E − e 1 − e ⋅ cos ⁡ E 1 + cos ⁡ E − e 1 − e ⋅ cos ⁡ E = 1 − e ⋅ cos ⁡ E − cos ⁡ E + e 1 − e ⋅ cos ⁡ E + cos ⁡ E − e = 1 + e 1 − e   ⋅   1 − cos ⁡ E 1 + cos ⁡ E = 1 + e 1 − e   ⋅   tan 2 ⁡ E 2

From the geometrical construction defining the eccentric anomaly it is clear that the vectors (   cos ⁡ E   ,   sin ⁡ E   ) and (   cos ⁡ θ   ,   sin ⁡ θ   ) are on the same side of the x-axis. From this then follows that the vectors ( cos ⁡ E 2   ,   sin ⁡ E 2 ) and ( cos ⁡ θ 2   ,   sin ⁡ θ 2 ) are in the same quadrant. One therefore has that

and that

where " arg ⁡ ( x   ,   y ) " is the polar argument of the vector (   x   ,   y   ) and n is selected such that | E − θ | < π

For the numerical computation of arg ⁡ ( x   ,   y ) the standard function ATAN2(y,x) (or in double precision DATAN2(y,x)) available in for example the programming language FORTRAN can be used.

Note that this is a mapping between the ranges

[ − ∞ < θ < ∞ ] ⟷ [ − ∞ < E < ∞ ]

For a hyperbolic orbit one gets from (28) and (29) that

and therefore that

As

tan 2 ⁡ θ 2 = 1 − cos ⁡ θ 1 + cos ⁡ θ = 1 − e − cosh ⁡ E e ⋅ cosh ⁡ E − 1 1 + e − cosh ⁡ E e ⋅ cosh ⁡ E − 1 = e ⋅ cosh ⁡ E − e + cosh ⁡ E e ⋅ cosh ⁡ E + e − cosh ⁡ E = e + 1 e − 1   ⋅   cosh ⁡ E − 1 cosh ⁡ E + 1 = e + 1 e − 1   ⋅   tanh 2 ⁡ E 2

and as tan ⁡ θ 2 and tanh ⁡ E 2 have the same sign it follows that

This relation is convenient for passing between "true anomaly" and the parameter E, the latter being connected to time through relation (34). Note that this is a mapping between the ranges

[ − cos − 1 ⁡ ( − 1 e ) < θ < cos − 1 ⁡ ( − 1 e ) ] ⟷ [ − ∞ < E < ∞ ]

and that E 2 can be computed using the relation

tanh − 1 ⁡ x = 1 2 ln ⁡ ( 1 + x 1 − x )

From relation (27) follows that the orbital period P for an elliptic orbit is

As the potential energy corresponding to the force field of relation (1) is

− μ r

it follows from (13), (14), (18) and (19) that the sum of the kinetic and the potential energy

V r 2 + V t 2 2 − μ r

for an elliptic orbit is

and from (13), (16), (18) and (19) that the sum of the kinetic and the potential energy for a hyperbolic orbit is

Relative the inertial coordinate system

x ^   ,   y ^

in the orbital plane with x ^ towards pericentre one gets from (18) and (19) that the velocity components are

See also Equation of the center – Analytical expansions
The Equation of the center relates mean anomaly to true anomaly for elliptical orbits, for small numerical eccentricity.

Determination of the Kepler orbit that corresponds to a given initial state

This is the "initial value problem" for the differential equation (1) which is a first order equation for the 6-dimensional "state vector" (   r ¯   , v ¯   ) when written as

For any values for the initial "state vector" (   r 0 ¯   , v 0 ¯   ) the Kepler orbit corresponding to the solution of this initial value problem can be found with the following algorithm:

Define the orthogonal unit vectors ( r ^   ,   t ^ ) through

with r > 0 and V t > 0

From (13), (18) and (19) follows that by setting

and by defining e ≥ 0 and θ such that

where

one gets a Kepler orbit that for true anomaly θ has the same r, V r and V t values as those defined by (50) and (51).

If this Kepler orbit then also has the same ( r ^   ,   t ^ ) vectors for this true anomaly θ as the ones defined by (50) and (51) the state vector ( r ¯   ,   v ¯ ) of the Kepler orbit takes the desired values (   r 0 ¯   , v 0 ¯   ) for true anomaly θ .

The standard inertially fixed coordinate system ( x ^   ,   y ^ ) in the orbital plane (with x ^ directed from the centre of the homogeneous sphere to the pericentre) defining the orientation of the conical section (ellipse, parabola or hyperbola) can then be determined with the relation

Note that the relations (53) and (54) has a singularity when V r = 0 and

V t = V 0 = μ p = μ ( r ⋅ V t ) 2 μ

i.e.

which is the case that it is a circular orbit that is fitting the initial state (   r 0 ¯   , v 0 ¯   )

The osculating Kepler orbit

For any state vector ( r ¯ , v ¯ ) the Kepler orbit corresponding to this state can be computed with the algorithm defined above. First the parameters p , e , θ are determined from r , V r , V t and then the orthogonal unit vectors in the orbital plane x ^ , y ^ using the relations (56) and (57).

If now the equation of motion is

where

F ¯ ⁡ ( r ¯ , r ¯ ˙ , t )

is a function other than

− μ ⋅ r ^ r 2

the resulting parameters

p , e , θ , x ^ , y ^

defined by r ¯ , r ¯ ˙ will all vary with time as opposed to the case of a Kepler orbit for which only the parameter θ will vary

The Kepler orbit computed in this way having the same "state vector" as the solution to the "equation of motion" (59) at time t is said to be "osculating" at this time.

This concept is for example useful in case

F ¯ ⁡ ( r ¯ , r ¯ ˙ , t ) = − μ ⋅ r ^ r 2 + f ¯ ⁡ ( r ¯ , r ¯ ˙ , t )

where

f ¯ ⁡ ( r ¯ , r ¯ ˙ , t )

is a small "perturbing force" due to for example a faint gravitational pull from other celestial bodies. The parameters of the osculating Kepler orbit will then only slowly change and the osculating Kepler orbit is a good approximation to the real orbit for a considerable time period before and after the time of osculation.

This concept can also be useful for a rocket during powered flight as it then tells which Kepler orbit the rocket would continue in case the thrust is switched off.

For a "close to circular" orbit the concept "eccentricity vector" defined as e ¯ = e ⋅ x ^ is useful. From (53), (54) and (56) follows that

i.e. e ¯ is a smooth differentiable function of the state vector ( r ¯ , v ¯ ) also if this state corresponds to a circular orbit.