Samiksha Jaiswal (Editor)

Proportionality (mathematics)

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Proportionality (mathematics)

In mathematics, two variables are proportional if a change in one is always accompanied by a change in the other, and if the changes are always related by use of a constant multiplier. The constant is called the coefficient of proportionality or proportionality constant.

Contents

  • If one variable is always the product of the other and a constant, the two are said to be directly proportional. x and y are directly proportional if the ratio y/x is constant.
  • If the product of the two variables is always a constant, the two are said to be inversely proportional. x and y are inversely proportional if the product xy is constant.

    • To express the statement "y is directly proportional to x" mathematically, we write an equation y = cx, where c is the proportionality constant. Symbolically, this is written as y ∝ x.

    To express the statement "y is inversely proportional to x" mathematically, we write an equation y = c/x. We can equivalently write "y is directly proportional to 1/x".

    An equality of two ratios is called a proportion. For example, a/c = b/d, where no term is zero.

    Direct proportionality

    Given two variables x and y, y is directly proportional to x if there is a non-zero constant k such that

    y = k x .

    The relation is often denoted, using the ∝ or ~ symbol, as

    y ∝ x

    and the constant ratio

    k = y x

    is called the proportionality constant, constant of variation or constant of proportionality.

    Examples

  • If an object travels at a constant speed, then the distance traveled is directly proportional to the time spent traveling, with the speed being the constant of proportionality.
  • The circumference of a circle is directly proportional to its diameter, with the constant of proportionality equal to π.
  • On a map drawn to scale, the distance between any two points on the map is directly proportional to the distance between the two locations that the points represent, with the constant of proportionality being the scale of the map.
  • The force acting on a certain object due to gravity is directly proportional to the object's mass; the constant of proportionality between the mass and the force is known as gravitational acceleration.

    • Properties

    Since

    y = k x

    is equivalent to

    x = ( 1 k ) y ,

    it follows that if y is directly proportional to x, with (nonzero) proportionality constant k, then x is also directly proportional to y with proportionality constant 1/k.

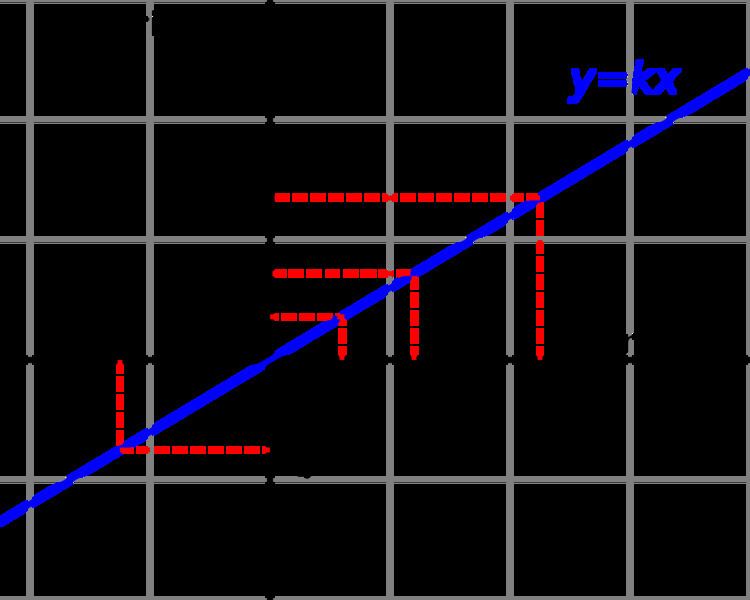
    If y is directly proportional to x, then the graph of y as a function of x is a straight line passing through the origin with the slope of the line equal to the constant of proportionality: it corresponds to linear growth.

    Inverse proportionality

    The concept of inverse proportionality can be contrasted against direct proportionality. Consider two variables said to be "inversely proportional" to each other. If all other variables are held constant, the magnitude or absolute value of one inversely proportional variable decreases if the other variable increases, while their product (the constant of proportionality k) is always the same.

    Formally, two variables are inversely proportional (also called varying inversely, in inverse variation, in inverse proportion, in reciprocal proportion) if each of the variables is directly proportional to the multiplicative inverse (reciprocal) of the other, or equivalently if their product is a constant. It follows that the variable y is inversely proportional to the variable x if there exists a non-zero constant k such that

    y = ( k x ) (Also sometimes written as: x y = k )

    The constant can be found by multiplying the original x variable and the original y variable.

    As an example, the time taken for a journey is inversely proportional to the speed of travel; the time needed to dig a hole is (approximately) inversely proportional to the number of people digging.

    The graph of two variables varying inversely on the Cartesian coordinate plane is a rectangular hyperbola. The product of the x and y values of each point on the curve equals the constant of proportionality (k). Since neither x nor y can equal zero (because k is non-zero), the graph never crosses either axis.

    Hyperbolic coordinates

    The concepts of direct and inverse proportion lead to the location of points in the Cartesian plane by hyperbolic coordinates; the two coordinates correspond to the constant of direct proportionality that locates a point on a ray and the constant of inverse proportionality that locates a point on a hyperbola.

    Exponential and logarithmic proportionality

    A variable y is exponentially proportional to a variable x, if y is directly proportional to the exponential function of x, that is if there exist non-zero constants k and a such that

    y = k a x .

    Likewise, a variable y is logarithmically proportional to a variable x, if y is directly proportional to the logarithm of x, that is if there exist non-zero constants k and a such that

    y = k log a ⁡ ( x ) .

    References

    Proportionality (mathematics) Wikipedia
    (Text) CC BY-SA


    Similar Topics