Glossary of algebraic topology

!$@

*

The base point of a based space.

X +

For an unbased space X, X₊ is the based space obtained by adjoining a disjoint base point.

A

absolute neighborhood retract

abstract

1.  Abstract homotopy theory

Adams

1.  John Frank Adams.2.  The Adams spectral sequence.3.  The Adams conjecture.4.  The Adams e-invariant.5.  The Adams operations.

Alexander duality

Alexander trick

The Alexander trick produces a section of the restriction map Top ⁡ ( D n + 1 ) → Top ⁡ ( S n ) , Top denoting a homeomorphism group; namely, the section is given by sending a homeomorphism f : S n → S n to the homeomorphism f ~ : D n + 1 → D n + 1 , 0 ↦ 0 , 0 ≠ x ↦ | x | f ( x / | x | ) .This section is in fact a homotopy inverse.

Analysis Situs

aspherical space

assembly map

Atiyah

1.  Michael Atiyah.2.  Atiyah duality.3.  The Atiyah–Hirzebruch spectral sequence.

B

bar construction

based space

A pair (X, x₀) consisting of a space X and a point x₀ in X.

Betti number

Bockstein homomorphism

Borel–Moore homology

Borsuk's theorem

Bott

1.  Raoul Bott.2.  The Bott periodicity theorem for unitary groups say: π q U = π q + 2 U , q ≥ 0 .3.  The Bott periodicity theorem for orthogonal groups say: π q O = π q + 8 O , q ≥ 0 .

Brouwer fixed point theorem

The Brouwer fixed point theorem says that any map f : D n → D n has a fixed point.

C

cap product

Čech cohomology

cellular

1.  A map ƒ:X→Y between CW complexes is cellular if f ( X n ) ⊂ Y n for all n.2.  The cellular approximation theorem says that every map between CW complexes is homotopic to a cellular map between them.3.  The cellular homology is the (canonical) homology of a CW complex. Note it applies to CW complexes and not to spaces in general. A cellular homology is highly computable; it is especially useful for spaces with natural cell decompositions like projective spaces or Grassmannian.

chain homotopy

Given chain maps f , g : ( C , d C ) → ( D , d D ) between chain complexes of modules, a chain homotopy s from f to g is a sequence of module homomorphisms s i : C i → D i + 1 satisfying f i − g i = d D ∘ s i + s i − 1 ∘ d C .

chain map

A chain map f : ( C , d C ) → ( D , d D ) between chain complexes of modules is a sequence of module homomorphisms f i : C i → D i that commutes with the differentials; i.e., d D ∘ f i = f i − 1 ∘ d C .

chain homotopy equivalence

A chain map that is an isomorphism up to chain homotopy; that is, if ƒ:C→D is a chain map, then it is a chain homotopy equivalence if there is a chain map g:D→C such that gƒ and ƒg are chain homotopic to the identity homomorphisms on C and D, respectively.

change of fiber

The change of fiber of a fibration p is a homotopy equivalence, up to homotopy, between the fibers of p induced by a path in the base.

character variety

The character variety of a group π and an algebraic group G (e.g., a reductive complex Lie group) is the geometric invariant theory quotient by G: X ( π , G ) = Hom ⁡ ( π , G ) / / G .

characteristic class

Let Vect(X) be the set of isomorphism classes of vector bundles on X. We can view X ↦ Vect ⁡ ( X ) as a contravariant functor from Top to Set by sending a map ƒ:X → Y to the pullback ƒ^* along it. Then a characteristic class is a natural transformation from Vect to the cohomology functor H^*. Explicitly, to each vector bundle E we assign a cohomology class, say, c(E). The assignment is natural in the sense that ƒ^*c(E) = c(ƒ^*E).

chromatic homotopy theory

chromatic homotopy theory.

class

1.  Chern class.2.  Stiefel–Whitney class.

classifying space

Loosely speaking, a classifying space is a space representing some contravariant functor defined on the category of spaces; for example, B U is the classifying space in the sense [ − , B U ] is the functor X ↦ Vect R ⁡ ( X ) that sends a space to the set of isomorphism classes of real vector bundles on the space.

clutching

cobar spectral sequence

cobordism

1.  See cobordism.2.  A cobordism ring is a ring whose elements are cobordism classes.3.  See also h-cobordism theorem, s-cobordism theorem.

coefficient ring

If E is a ring spectrum, then the coefficient ring of it is the ring π ∗ E .

cofiber sequence

A cofiber sequence is any sequence that is equivalent to the sequence X → f Y → C f for some ƒ where C f is the reduced mapping cone of ƒ (called the cofiber of ƒ).

cofibrant approximation

cofibration

A map i : A → B is a cofibration if it satisfies the property: given h 0 : B → X and homotopy g t : A → X , there is a homotopy h t : B → X such that h t ∘ i = g t . A cofibration is injective and is a homeomorphism onto its image.

coherent homotopy

cohomotopy group

For a based space X, the set of homotopy classes [ X , S n ] is called the n-th cohomotopy group of X.

cohomology operation

completion

complex bordism

complex-oriented

A multiplicative cohomology theory E is complex-oriented if the restriction map E²(CP^∞) → E²(CP¹) is surjective.

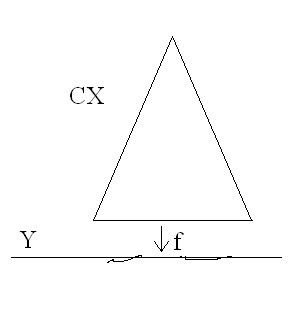
cone

The cone over a space X is C X = X × I / X × { 0 } . The reduced cone is obtained from the reduced cylinder X ∧ I + by collapsing the top.

connective

A spectrum E is connective if π q E = 0 for all negative integers q.

configuration space

contractible space

A space is contractible if the identity map on the space is homotopic to the constant map.

covering

1.  A map p: Y → X is a covering or a covering map if each point of x has a neighborhood N that is evenly covered by p; this means that the pre-image of N is a disjoint union of open sets, each of which maps to N homeomorphically.2.  It is n-sheeted if each fiber p⁻¹(x) has exactly n elements.3.  It is universal if Y is simply connected.4.  A morphism of a covering is a map over X. In particular, an automorphism of a covering p:Y→X (also called a deck transformation) is a map Y→Y over X that has inverse; i.e., a homeomorphism over X.5.  A G-covering is a covering arising from a group action on a space X by a group G, the covering map being the quotient map from X to the orbit space X/G. The notion is used to state the universal property: if X admits a universal covering (in particular connected), thenIn particular, if G is abelian, then the left-hand side is Hom ⁡ ( π 1 ( X , x 0 ) , G ) = H 1 ⁡ ( X ; G ) (cf. nonabelian cohomology.)

cup product

CW complex

A CW complex is a space X equipped with a CW structure; i.e., a filtrationsuch that (1) X⁰ is discrete and (2) Xⁿ is obtained from X^n-1 by attaching n-cells.

cyclic homology

D

deck transformation

Another term for an automorphism of a covering.

delooping

degeneracy cycle

degree

E

Eckmann–Hilton argument

The Eckmann–Hilton argument.

Eckmann–Hilton duality

Eilenberg–MacLane spaces

Given an abelian group π, the Eilenberg–MacLane spaces K ( π , n ) are characterized by π q K ( π , n ) = { π if  q = n 0 otherwise .

Eilenberg–Steenrod axioms

The Eilenberg–Steenrod axioms are the set of axioms that any cohomology theory (singular, cellular, etc.) must satisfy. Weakening the axioms (namely dropping the dimension axiom) leads to a generalized cohomology theory.

Eilenberg–Zilber theorem

E_n-algebra

equivariant algebraic topology

Equivariant algebraic topoloy is the study of spaces with (continuous) group action.

exact

A sequence of pointed sets X → f Y → g Z is exact if the image of f coincides with the pre-image of the chosen point of Z.

excision

The excision axiom for homology says: if U ⊂ X and U ¯ ⊂ int ⁡ ( A ) , then for each q,is an isomorphism.

excisive pair/triad

F

factorization homology

fiber-homotopy equivalence

Given D→B, E→B, a map ƒ:D→E over B is a fiber-homotopy equivalence if it is invertible up to homotopy over B. The basic fact is that if D→B, E→B are fibrations, then a homotopy equivalence from D to E is a fiber-homotopy equivalence.

fibration

A map p:E → B is a fibration if for any given homotopy g t : X → B and a map h 0 : X → E such that p ∘ h 0 = g 0 , there exists a homotopy h t : X → E such that p ∘ h t = g t . (The above property is called the homotopy lifting property.) A covering map is a basic example of a fibration.

fibration sequence

One says F → X → p B is a fibration sequence to mean that p is a fibration and that F is homotopy equivalent to the homotopy fiber of p, with some understanding of base points.

finitely dominated

fundamental class

fundamental group

The fundamental group of a space X with base point x₀ is the group of homotopy classes of loops at x₀. It is precisely the first homotopy group of (X, x₀) and is thus denoted by π 1 ( X , x 0 ) .

fundamental groupoid

The fundamental groupoid of a space X is the category whose objects are the points of X and whose morphisms x → y are the homotopy classes of paths from x to y; thus, the set of all morphisms from an object x₀ to itself is, by definition, the fundament group π 1 ( X , x 0 ) .

free

Synonymous with unbased. For example, the free path space of a space X refers to the space of all maps from I to X; i.e., X I while the path space of a based space X consists of such map that preserve the base point (i.e., 0 goes to the base point of X).

Freudenthal suspension theorem

For a nondegenerately based space X, the Freudenthal suspension theorem says: if X is (n-1)-connected, then the suspension homomorphism π q X → π q + 1 Σ X is bijective for q < 2n - 1 and is surjective if q = 2n - 1.

G

G-fibration

A G-fibration with some topological monoid G. An example is Moore's path space fibration.

Γ-space

generalized cohomology theory

A generalized cohomology theory is a contravariant functor from the category of pairs of spaces to the category of abelian groups that satisfies all of the Eilenberg–Steenrod axioms except the dimension axiom.

genus

group completion

grouplike

An H-space X is said to be group-like or grouplike if π 0 X is a group; i.e., X satisfies the group axioms up to homotopy.

Gysin sequence

H

Hilton–Milnor theorem

The Hilton–Milnor theorem.

H-space

An H-space is a based space that is a unital magma up to homotopy.

homologus

Two cycles are homologus if they belong to the same homology class.

homotopy category

Let C be a subcategory of the category of all spaces. Then the homotopy category of C is the category whose class of objects is the same as the class of objects of C but the set of morphisms from an object x to an object y is the set of the homotopy classes of morphisms from x to y in C. For example, a map is a homotopy equivalence if and only if it is an isomorphism in the homotopy category.

homotopy colimit

homotopy over a space B

A homotopy h_t such that for each fixed t, h_t is a map over B.

homotopy equivalence

1.  A map ƒ:X→Y is a homotopy equivalence if it is invertible up to homotopy; that is, there exists a map g: Y→X such that g ∘ ƒ is homotopic to th identity map on X and ƒ ∘ g is homotopic to the identity map on Y.2.  Two spaces are said to be homotopy equivalent if there is a homotopy equivalence between the two. For example, by definition, a space is contractible if it is homotopy equivalent to a point space.

homotopy excision theorem

The homotopy excision theorem is a substitute for the failure of excision for homotopy groups.

homotopy fiber

The homotopy fiber of a based map ƒ:X→Y, denoted by Fƒ, is the pullback of P Y → Y , χ ↦ χ ( 1 ) along f.

homotopy fiber product

A fiber product is a particular kind of a limit. Replacing this limit lim with a homotopy limit holim yields a homotopy fiber product.

homotopy group

1.  For a based space X, let π n X = [ S n , X ] , the set of homotopy classes of based maps. Then π 0 X is the set of path-connected components of X, π 1 X is the fundamental group of X and π n X , n ≥ 2 are the (higher) n-th homotopy groups of X.2.  For based spaces A ⊂ X , the relative homotopy group π n ( X , A ) is defined as π n − 1 of the space of paths that all start at the base point of X and end somewhere in A. Equivalently, it is the π n − 1 of the homotopy fiber of A ↪ X .3.  If E is a spectrum, then π k E = lim → n ⁡ π k + n E n . 4.  If X is a based space, then the stable k-th homotopy group of X is π k s X = lim → n ⁡ π k + n Σ n X . In other words, it is the k-th homotopy group of the suspension spectrum of X.

homotopy quotient

If G is a Lie group acting on a manifold X, then the quotient space ( E G × X ) / G is called the homotopy quotient (or Borel construction) of X by G, where EG is the universal bundle of G.

homotopy spectral sequence

homotopy sphere

Hopf

1.  Heinz Hopf.2.  Hopf invariant.3.  The Hopf index theorem.4.  Hopf construction.

Hurewicz

The Hurewicz theorem establishes a relationship between homotopy groups and homology groups.

I

infinite loop space

infinite loop space machine

infinite mapping telescope

integration along the fiber

isotopy

J

J-homomorphism

See J-homomorphism.

join

The join of based spaces X, Y is X ⋆ Y = Σ ( X ∧ Y ) .

K

k-invariant

Kan complex

See Kan complex.

Kervaire invariant

The Kervaire invariant.

Koszul duality

Koszul duality.

Künneth formula

L

Lazard ring

The Lazard ring L is the (huge) commutative ring together with the formal group law ƒ that is universal among all the formal group laws in the sense that any formal group law g over a commutative ring R is obtained via a ring homomorphism L → R mapping ƒ to g. According to Quillen's theorem, it is also the coefficient ring of the complex bordism MU. The Spec of L is called the moduli space of formal group laws.

Lefschetz fixed point theorem

The Lefschetz fixed point theorem says: given a finite simplicial complex K and its geometric realization X, if a map f : X → X has no fixed point, then the Lefschetz number of f; that is, ∑ 0 ∞ ( − 1 ) q tr ⁡ ( f ∗ : H q ⁡ ( X ) → H q ⁡ ( X ) ) is zero. For example, it implies the Brouwer fixed point theorem since the Lefschetz number of f : D n → D n is, as higher homologies vanish, one.

lens space

The lens space is the quotient space { z ∈ C n | | z | = 1 } / μ p where μ p is the group of p-th roots of unity acting on the unit sphere by ζ ⋅ ( z 1 , … , z n ) = ( ζ z 1 , … , ζ z n ) .

Leray spectral sequence

local coefficient

1.  A module over the group ring Z [ π 1 B ] for some based space B; in other words, an abelian group together with a homomorphism π 1 B → Aut ⁡ ( A ) .2.  The local coefficient system over a based space B with an abelian group A is a fiber bundle over B with discrete fiber A. If B admits a universal covering B ~ , then this meaning coincides with that of 1. in the sense: every local coefficient system over B can be given as the associated bundle B ~ × π 1 B A .

local sphere

The localization of a sphere at some prime number

localization

loop space

The loop space Ω X of a based space X is the space of all loops starting and ending at the base point of X.

M

Madsen–Weiss theorem

mapping

1.  The mapping cone (or cofiber) of a map ƒ:X→Y is C f = Y ∪ f C X .2.  The mapping cylinder of a map ƒ:X→Y is M f = Y ∪ f ( X × I ) . Note: C f = M f / ( X × { 0 } ) .3.  The reduced versions of the above are obtained by using reduced cone and reduced cylinder.4.  The mapping path space P_p of a map p:E→B is the pullback of B I → B along p. If p is fibration, then the natural map E→P_p is a fiber-homotopy equivalence; thus, roughly speaking, one can replace E by the mapping path space without changing the homotopy type of the fiber.

Mayer–Vietoris sequence

model category

A presentation of an ∞-category. See also model category.

Moore space

multiplicative

A generalized cohomology theory E is multiplicative if E^*(X) is a graded ring. For example, the ordinary cohomology theory and the complex K-theory are multiplicative (in fact, cohomology theories defined by E_∞-rings are multiplicative.)

N

n-cell

Another term for an n-disk.

n-connected

A based space X is n-connected if π q X = 0 for all integers q ≤ n. For example, "1-connected" is the same thing as "simply connected".

n-equivalent

NDR-pair

A pair of spaces A ⊂ X is said to be an NDR-pair (=neighborhood deformation retract pair) if there is a map u : X → I and a homotopy h t : X → X such that A = u − 1 ( 0 ) , h 0 = id X , h t | A = id A and h 1 ( { x | u ( x ) < 1 } ) ⊂ A .
If A is a closed subspace of X, then the pair A ⊂ X is an NDR-pair if and only if A ↪ X is a cofibration.

nilpotent

1.  nilpotent space; for example, a simply connected space is nilpotent.2.  The nilpotent theorem.

normalized

Given a simplicial group G, the normalized chain complex NG of G is given by ( N G ) n = ∩ 1 ∞ ker ⁡ d i n with the n-th differential given by d 0 n ; intuitively, one throws out degenerate chains. It is also called the Moore complex.

O

obstruction cocycle

obstruction theory

Obstruction theory is the collection of constructions and calculations indicating when some map on a submanifold (subcomplex) can or cannot be extended to the full manifold. These typically involve the Postnikov tower, killing homotopy groups, obstruction cocycles, etc.

of finite type

A CW complex is of finite type if there are only finitely many cells in each dimension.

operad

The portmanteau of “operations” and “monad”. See operad.

orbit category

orientation

1.  The orientation covering (or orientation double cover) of a manifold is a two-sheeted covering so that each fiber over x corresponds to two different ways of orienting a neighborhood of x.2.  An orientation of a manifold is a section of an orientation covering; i.e., a consistent choice of a point in each fiber.3.  An orientation character (also called the first Stiefel–Whitney class) is a group homomorphism π 1 ( X , x 0 ) → { ± 1 } that corresponds to an orientation covering of a manifold X (cf. #covering.)4.  See also orientation of a vector bundle as well as orientation sheaf.

P

p-adic homotopy theory

The p-adic homotopy theory.

path class

An equivalence class of paths (two paths are equivalent if they are homotopic to each other).

path lifting

A path lifting function for a map p: E → B is a section of E I → P p where P p is the mapping path space of p. For example, a covering is a fibration with a unique path lifting function. By formal consideration, a map is a fibration if and only if there is a path lifting function for it.

path space

The path space of a based space X is P X = Map ⁡ ( I , X ) , the space of based maps, where the base point of I is 0. Put in another way, it is the (set-theoretic) fiber of X I → X , χ ↦ χ ( 0 ) over the base point of X. The projection P X → X , χ ↦ χ ( 1 ) is called the path space fibration, whose fiber over the base point of X is the loop space Ω X . See also #mapping path space.

phantom map

Poincaré

The Poincaré duality theorem says: given a manifold M of dimension n and an abelian group A, there is a natural isomorphism H c ∗ ⁡ ( M ; A ) ≃ H n − ∗ ⁡ ( M ; A ) .

Pontrjagin–Thom construction

Postnikov system

A Postnikov system is a sequence of fibrations, such that all preceding manifolds have vanishing homotopy groups below a given dimension.

principal fibration

Usually synonymous with G-fibration.

profinite

profinite homotopy theory; it studies profinite spaces.

properly discontinuous

Not particularly a precise term. But it could mean, for example, that G is discrete and each point of the G-space has a neighborhood V such that for each g in G that is not the identity element, gV intersects V at finitely many points.

pullback

Given a map p:E→B, the pullback of p along ƒ:X→B is the space f ∗ E = { ( e , x ) ∈ E × X | p ( e ) = f ( x ) } (succinctly it is the equalizer of p and f). It is a space over X through a projection.

Puppe sequence

The Puppe sequence refers ro either of the sequenceswhere C f , F f are homotopy cofiber and homotopy fiber of f.

pushout

Given A ⊂ B and a map f : A → X , the pushout of X and B along f isthat is X and B are glued together along A through f. The map f is usually called the attaching map.The important example is when B = Dⁿ, A = S^n-1; in that case, forming such a pushout is called attaching an n-cell (meaning an n-disk) to X.

Q

quasi-fibration

Quillen

1.  Daniel Quillen2.  Quillen’s theorem says that π ∗ M U is the Lazard ring.

R

rational

1.  The rational homotopy theory.2.  The rationalization of a space X is, roughly, the localization of X at zero. More precisely, X₀ together with j: X → X₀ is a rationalization of X if the map π ∗ X ⊗ Q → π ∗ X 0 ⊗ Q induced by j is an isomorphism of vector spaces and π ∗ X 0 ⊗ Q ≃ π ∗ X 0 .3.  The rational homotopy type of X is the weak homotopy type of X₀.

Reidemeister

Reidemeister torsion.

reduced

The reduced suspension of a based space X is the smash product Σ X = X ∧ S 1 . It is related to the loop functor by Map ⁡ ( Σ X , Y ) = Map ⁡ ( X , Ω Y ) where Ω Y = Map ⁡ ( S 1 , Y ) is the loop space.

ring spectrum

A ring spectrum is a spectrum that satisfying the ring axioms, either on nose or up to homotopy. For example, a complex K-theory is a ring spectrum.

S

Samelson product

Serre

1.  Jean-Pierre Serre.2.  Serre class.3.  Serre spectral sequence.

simple

simple-homotopy equivalence

A map ƒ:X→Y between finite simplicial complexes (e.g., manifolds) is a simple-homotopy equivalence if it is homotopic to a composition of finitely many elementary expansions and elementary collapses. A homotopy equivalence is a simple-homotopy equivalence if and only if its Whitehead torsion vanishes.

simplicial approximation

See simplicial approximation theorem.

simplicial complex

See simplicial complex; the basic example is a triangulation of a manifold.

simplicial homology

A simplicial homology is the (canonical) homology of a simplicial complex. Note it applies to simplicial complexes and not to spaces; cf. #singular homology.

signature invariant

singular

1.  Given a space X and an abelian group π, the singular homology group of X with coefficients in π is H ∗ ⁡ ( X ; π ) = H ∗ ⁡ ( C ∗ ( X ) ⊗ π ) where C ∗ ( X ) is the singular chain complex of X; i.e., the n-th degree piece is the free abelian group generated by all the maps △ n → X from the standard n-simplex to X. A singular homology is a special case of a simplicial homology; indeed, for each space X, there is the singular simplicial complex of X whose homology is the singular homology of X.2.  The singular simplices functor is the functor T o p → s S e t from the category of all spaces to the category of simplicial sets, that is the right adjoint to the geometric realization functor.3.  The singular simplicial complex of a space X is the normalized chain complex of the singular simplex of X.

slant product

small object argument

smash product

The smash product of based spaces X, Y is X ∧ Y = X × Y / X ∨ Y . It is characterized by the adjoint relation Map ⁡ ( X ∧ Y , Z ) = Map ⁡ ( X , Map ⁡ ( Y , Z ) ) .

Spanier–Whitehead

The Spanier–Whitehead duality.

spectrum

Roughly a sequence of spaces together with the maps (called the structure maps) between the consecutive terms; see spectrum (topology).

sphere spectrum

The sphere spectrum is a spectrum consisting of a sequence of spheres S 0 , S 1 , S 2 , S 3 , … together with the maps between the spheres given by suspensions. In short, it is the suspension spectrum of S 0 .

stable homotopy group

See #homotopy group.

Steenrod homology

Steenrod homology.

Steenrod operation

Sullivan

1.  Dennis Sullivan.2.  The Sullivan conjecture.3.  Infinitesimal computations in topology, 1977  - introduces rational homotopy theory (along with Quillen's paper).4.  The Sullivan algebra in the rational homotopy theory.

suspension spectrum

The suspension spectrum of a based space X is the spectrum given by X n = Σ n X .

symmetric spectrum

T

Thom

1.  René Thom.2.  If E is a vector bundle on a paracompact space X, then the Thom space Th ( E ) of E is obtained by first replacing each fiber by its compactification and then collapsing the base X.3.  The Thom isomorphism says: for each orientable vector bundle E of rank n on a manifold X, a choice of an orientation (the Thom class of E) induces an isomorphism H ~ ∗ + n ( Th ( E ) ; Z ) ≃ H ∗ ⁡ ( X ; Z ) .

topological chiral homology

transfer

transgression

U

universal coefficient

The universal coefficient theorem.

up to homotopy

A statement holds in the homotopy category as opposed to the category of spaces.

V

van Kampen

The van Kampen theorem says: if a space X is path-connected and if x₀ is a point in X, then π 1 ( X , x 0 ) = lim → ⁡ π 1 ( U , x 0 ) where the colimit runs over some open cover of X consisting of path-connected open subsets containing x₀ such that the cover is closed under finite intersections.

W

Waldhausen S-construction

Waldhausen S-construction.

Wall's finiteness obstruction

weak equivalence

A map ƒ:X→Y of based spaces is a weak equivalence if for each q, the induced map f ∗ : π q X → π q Y is bijective.

wedge

For based spaces X, Y, the wedge product X ∧ Y of X and Y is the coproduct of X and Y; concretely, it is obtained by taking their disjoint union and then identifying the respective base points.

well pointed

A based space is well pointed (or non-degenerately based) if the inclusion of the base point is a cofibration.

Whitehead

1.  J. H. C. Whitehead.2.  Whitehead's theorem says that for CW complexes, the homotopy equivalence is the same thing as the weak equivalence.3.  Whitehead group.4.  Whitehead product.

winding number