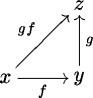
Glossary of category theory - Alchetron, the free social encyclopedia

This is a glossary of properties and concepts in category theory in mathematics.

A

abelian

A category is abelian if it has a zero object, it has all pullbacks and pushouts, and all monomorphisms and epimorphisms are normal.

accessible

1. Given a cardinal number κ, an object X in a category is κ-accessible (or κ-compact or κ-presentable) if Hom ⁡ ( X , − ) commutes with κ-filtered colimits.2. Given a regular cardinal κ, a category is κ-accessible if it has κ-filtered colimits and there exists a small set S of κ-compact objects that generates the category under colimits, meaning every object can be written as a colimit of diagrams of objects in S.

additive

A category is additive if it is preadditive (to be precise, has some pre-additive structure) and admits all finite coproducts. Although "preadditive" is an additional structure, one can show "additive" is a property of a category; i.e., one can ask whether a given category is additive or not.

adjunction

An adjunction (also called an adjoint pair) is a pair of functors F: C → D, G: D → C such that there is a "natural" bijection Hom D ⁡ ( F ( X ) , Y ) ≃ Hom C ⁡ ( X , G ( Y ) ) ;F is said to be left adjoint to G and G to right adjoint to F. Here, "natural" means there is a natural isomorphism Hom D ⁡ ( F ( − ) , − ) ≃ Hom C ⁡ ( − , G ( − ) ) of bifunctors (which are contravariant in the first variable.)

algebra for a monad

Given a monad T in a category X, an algebra for T or a T-algebra is an object in X with a monoid action of T ("algebra" is misleading and "T-object" is perhaps a better term.) For example, given a group G that determines a monad T in Set in the standard way, a T-algebra is a set with an action of G.

amnestic

A functor is amnestic if it has the property: if k is an isomorphism and F(k) is an identity, then k is an identity.

B

balanced

A category is balanced if every bimorphism is an isomorphism.

Beck's theorem

Beck's theorem characterizes the category of algebras for a given monad.

bifunctor

A bifunctor from a pair of categories C and D to a category E is a functor C × D → E. For example, for any category C, Hom ⁡ ( − , − ) is a bifunctor from C^op and C to Set.

bimorphism

A bimorphism is a morphism that is both an epimorphism and a monomorphism.

Bousfield localization

See Bousfield localization.

C

calculus of functors

The calculus of functors is a technique of studying functors in the manner similar to the way a function is studied via its Taylor series expansion; whence, the term "calculus".

cartesian closed

A category is cartesian closed if it has a terminal object and that any two objects have a product and exponential.

cartesian morphism

1. Given a functor π: C → D (e.g., a prestack over schemes), a morphism f: x → y in C is π-cartesian if, for each object z in C, each morphism g: z → y in C and each morphism v: π(z) → π(x) in D such that π(g) = π(f) ∘ v, there exists a unique morphism u: z → x such that π(u) = v and g = f ∘ u.2. Given a functor π: C → D (e.g., a prestack over rings), a morphism f: x → y in C is π-coCartesian if, for each object z in C, each morphism g: x → z in C and each morphism v: π(y) → π(z) in D such that π(g) = v ∘ π(f), there exists a unique morphism u: y → z such that π(u) = v and g = u ∘ f. (In short, f is the dual of a π-cartesian morphism.)

Cartesian square

A commutative diagram that is isomorphic to the diagram given as a fiber product.

categorification

The term "categorification" is an informal term referring to a process of replacing sets and set-theoretic concepts with categories and category-theoretic concepts in some nontrivial way to capture categoric flavors. Decategorification is the reverse of categorification.

D

Day convolution

Given a group or monoid M, the Day convolution is the tensor product in F c t ( M , S e t ) .

diagonal functor

Given categories I, C, the diagonal functor is the functor Δ : C → F c t ( I , C ) , A ↦ Δ A that sends each object A to the constant functor with value A and each morphism f : A → B to the natural transformation Δ f , i : Δ A ( i ) = A → Δ B ( i ) = B that is f at each i.

differential graded category

A differential graded category is a category whose Hom sets are equipped with structures of differential graded modules. In particular, if the category has only one object, it is the same as a differential graded module.

discrete

A category is discrete if each morphism is an identity morphism (of some object). For example, a set can be viewed as a discrete category.

E

Eilenberg–Moore category

Another name for the category of algebras for a given monad.

end

The end of a functor F : C op × C → X is the limit ∫ c ∈ C F ( c , c ) = lim ← ⁡ ( F # : C # → X ) where C # is the category (called the subdivision category of C) whose objects are symbols c # , u # for all objects c and all morphisms u in C and whose morphisms are b # → u # and u # → c # if u : b → c and where F # is induced by F so that c # would go to F ( c , c ) and u # , u : b → c would go to F ( b , c ) . For example, for functors F , G : C → X , ∫ c ∈ C Hom ⁡ ( F ( c ) , G ( c ) ) is the set of natural transformations from F to G. For more examples, see this mathoverflow thread. The dual of an end is a coend.

endofunctor

A functor between the same category.

enriched category

Given a monoidal category (C, ⊗, 1), a category enriched over C is, informally, a category whose Hom sets are in C. More precisely, a category D enriched over C is a data consisting of

A class of objects,
For each pair of objects X, Y in D, an object Map D ⁡ ( X , Y ) in C, called the mapping object from X to Y,
For each triple of objects X, Y, Z in D, a morphism in C, ∘ : Map D ⁡ ( Y , Z ) ⊗ Map D ⁡ ( X , Y ) → Map D ⁡ ( X , Z ) ,called the composition,
For each object X in D, a morphism 1 X : 1 → Map D ⁡ ( X , X ) in C, called the unit morphism of X

subject to the conditions that (roughly) the compositions are associative and the unit morphisms act as the multiplicative identity. For example, a category enriched over sets is an ordinary category.

empty

The empty category is a category with no object. It is the same thing as the empty set when the empty set is viewed as a discrete category.

epimorphism

A morphism f is an epimorphism if g = h whenever g ∘ f = h ∘ f . In other words, f is the dual of a monomorphism.

equalizer

The equalizer of a pair of morphisms f , g : A → B is the limit of the pair. It is the dual of a coequalizer.

equivalence

1. A functor is an equivalence if it is faithful, full and essentially surjective.2. A morphism in an ∞-category C is an equivalence if it gives an isomorphism in the homotopy category of C.

equivalent

A category is equivalent to another category if there is an equivalence between them.

essentially surjective

A functor F is called essentially surjective (or isomorphism-dense) if for every object B there exists an object A such that F(A) is isomorphic to B.

F

faithful

A functor is faithful if it is injective when restricted to each hom-set.

fibered category

A functor π: C → D is said to exhibit C as a category fibered over D if, for each morphism g: x → π(y) in D, there exists a π-cartesian morphism f: x' → y in C such that π(f) = g. If D is the category of affine schemes (say of finite type over some field), then π is more commonly called a prestack. Note: π is often a forgetful functor and in fact the Grothendieck construction implies that every fibered category can be taken to be that form (up to equivalences in a suitable sense).

fiber product

Given a category C and a set I, the fiber product over an object S of a family of objects X_i in C indexed by I is the product of the family in the slice category C / S of C over S (provided there are X i → S ). The fiber product of two objects X and Y over an object S is denoted by X × S Y and is also called a Cartesian square.

filtered

1. A filtered category (also called a filtrant category) is a nonempty category with the properties (1) given objects i and j, there are an object k and morphisms i → k and j → k and (2) given morphisms u, v: i → j, there are an object k and a morphism w: j → k such that w ∘ u = w ∘ v. A category I is filtered if and only if, for each finite category J and functor f: J → I, the set lim ← ⁡ Hom ⁡ ( f ( j ) , i ) is nonempty for some object i in I.2. Given a cardinal number π, a category is said to be π-filtrant if, for each category J whose set of morphisms has cardinal number strictly less than π, the set lim ← ⁡ Hom ⁡ ( f ( j ) , i ) is nonempty for some object i in I.

finitary monad

A finitary monad or an algebraic monad is a monad on Set whose underlying endofunctor commutes with filtered colimits.

finite

A category is finite if it has only finitely many morphisms.

forgetful functor

The forgetful functor is, roughly, a functor that loses some of data of the objects; for example, the functor G r p → S e t that sends a group to its underlying set and a group homomorphism to itself is a forgetful functor.

Frobenius category

A Frobenius category is an exact category that has enough injectives and enough projectives and such that the class of injective objects coincides with that of projective objects.

Fukaya category

See Fukaya category.

full

1. A functor is full if it is surjective when restricted to each hom-set.2. A category A is a full subcategory of a category B if the inclusion functor from A to B is full.

functor

Given categories C, D, a functor F from C to D is a structure-preserving map from C to D; i.e., it consists of an object F(x) in D for each object x in C and a morphism F(f) in D for each morphism f in C satisfying the conditions: (1) F ( f ∘ g ) = F ( f ) ∘ F ( g ) whenever f ∘ g is defined and (2) F ( id x ) = id F ( x ) . For example, P : S e t → S e t , S ↦ P ( S ) ,where P ( S ) is the power set of S is a functor if we define: for each function f : S → T , P ( f ) : P ( S ) → P ( T ) by P ( f ) ( A ) = f ( A ) .

functor category

The functor category Fct(C, D) from a category C to a category D is the category where the objects are all the functors from C to D and the morphisms are all the natural transformations between the functors.

G

Gabriel–Popescu theorem

The Gabriel–Popescu theorem says an abelian category is a quotient of the category of modules.

generator

In a category C, a family of objects G i , i ∈ I is a system of generators of C if the functor X ↦ ∏ i ∈ I Hom ⁡ ( G i , X ) is conservative. Its dual is called a system of cogenerators.

Grothendieck category

A Grothendieck category is a certain well-behaved kind of an abelian category.

Grothendieck construction

Given a functor U : C → C a t , let D_U be the category where the objects are pairs (x, u) consisting of an object x in C and an object u in the category U(x) and a morphism from (x, u) to (y, v) is a pair consisting of a morphism f: x → y in C and a morphism U(f)(u) → v in U(y). The passage from U to D_U is then called the Grothendieck construction.

Grothendieck fibration

A fibered category.

groupoid

1. A category is called a groupoid if every morphism in it is an isomorphism.2. An ∞-category is called an ∞-groupoid if every morphism in it is an equivalence (or equivalently if it is a Kan complex.)

H

Hall algebra of a category

See Ringel–Hall algebra.

heart

The heart of a t-structure ( D ≥ 0 , D ≤ 0 ) on a triangulated category is the intersection D ≥ 0 ∩ D ≤ 0 . It is an abelian category.

homological dimension

The homological dimension of an abelian category with enough injectives is the least non-negative intege n such that every object in the category admits an injective resolution of length at most n. The dimension is ∞ if no such integer exists. For example, the homological dimension of Mod_R with a principal ideal domain R is at most one.

homotopy category

See homotopy category. It is closely related to a localization of a category.

I

identity

1. The identity morphism f of an object A is a morphism from A to A such that for any morphisms g with domain A and h with codomain A, g ∘ f = g and f ∘ h = h .2. The identity functor on a category C is a functor from C to C that sends objects and morphisms to themselves.3. Given a functor F: C → D, the identity natural transformation from F to F is a natural transformation consisting of the identity morphisms of F(X) in D for the objects X in C.

image

The image of a morphism f: X → Y is the equalizer of Y ⇉ Y ⊔ X Y .

ind-limit

A colimit (or inductive limit) in F c t ( C op , S e t ) .

∞-category

An ∞-category C is a simplicial set satisfying the following condition: for each 0 < i < n,

every map of simplicial sets f : Λ i n → C extends to an n-simplex f : Δ n → C

where Δⁿ is the standard n-simplex and Λ i n is obtained from Δⁿ by removing the i-th face and the interior (see Kan fibration#Definition). For example, the nerve of a category satisfies the condition and thus can be considered as an ∞-category.

initial

1. An object A is initial if there is exactly one morphism from A to each object; e.g., empty set in Set.2. An object A in an ∞-category C is initial if Map C ⁡ ( A , B ) is contractible for each object B in C.

injective

An object A in an abelian category is injective if the functor Hom ⁡ ( − , A ) is exact. It is the dual of a projective object.

internal Hom

Given a monoidal category (C, ⊗), the internal Hom is a functor [ − , − ] : C op × C → C such that [ Y , − ] is the right adjoint to − ⊗ Y for each object Y in C. For example, the category of modules over a commutative ring R has the internal Hom given as [ M , N ] = Hom R ⁡ ( M , N ) , the set of R-linear maps.

inverse

A morphism f is an inverse to a morphism g if g ∘ f is defined and is equal to the identity morphism on the codomain of g, and f ∘ g is defined and equal to the identity morphism on the domain of g. The inverse of g is unique and is denoted by g⁻¹. f is a left inverse to g if f ∘ g is defined and is equal to the identity morphism on the domain of g, and similarly for a right inverse.

isomorphic

1. An object is isomorphic to another object if there is an isomorphism between them.2. A category is isomorphic to another category if there is an isomorphism between them.

isomorphism

A morphism f is an isomorphism if there exists an inverse of f.

K

Kleisli category

Given a monad T, the Kleisli category of T is the full subcategory of the category of T-algebras (called Eilenberg–Moore category) that consists of free T-algebras.

L

length

An object in an abelian category is said to have finite length if it has a composition series. The maximum number of proper subobjects in any such composition series is called the length of A.

limit

1. The limit (or projective limit) of a functor f : I op → S e t is2. The limit lim ← i ∈ I ⁡ f ( i ) of a functor f : I op → C is an object, if any, in C that satisfies: for any object X in C, Hom ⁡ ( X , lim ← i ∈ I ⁡ f ( i ) ) = lim ← i ∈ I ⁡ Hom ⁡ ( X , f ( i ) ) ; i.e., it is an object representing the functor X ↦ lim ← i ⁡ Hom ⁡ ( X , f ( i ) ) . 3. The colimit (or inductive limit) lim → i ∈ I ⁡ f ( i ) is the dual of a limit; i.e., given a functor f : I → C , it satisfies: for any X, Hom ⁡ ( lim → ⁡ f ( i ) , X ) = lim ← ⁡ Hom ⁡ ( f ( i ) , X ) . Explicitly, to give lim → ⁡ f ( i ) → X is to give a family of morphisms f ( i ) → X such that for any i → j , f ( i ) → X is f ( i ) → f ( j ) → X . Perhaps the simplest example of a colimit is a coequalizer. For another example, take f to be the identity functor on C and suppose L = lim → X ∈ C ⁡ f ( X ) exists; then the identity morphism on L corresponds to a compatible family of morphisms α X : X → L such that α L is the identity. If f : X → L is any morphism, then f = α L ∘ f = α X ; i.e., L is a final object of C.

localization of a category

See localization of a category.

M

monad

A monad in a category X is a monoid object in the monoidal category of endofunctors of X with the monoidal structure given by composition. For example, given a group G, define an endofunctor T on Set by T ( X ) = G × X . Then define the multiplication μ on T as the natural transformation μ : T ∘ T → T given by μ X : G × ( G × X ) → G × X , ( g , ( h , x ) ) ↦ ( g h , x ) and also define the identity map η in the analogous fashion. Then (T, μ, η) constitutes a monad in Set. More substantially, an adjunction between functors F : X ⇄ A : G determines a monad in X; namely, one takes T = G ∘ F , the identity map η on T to be a unit of the adjunction and also defines μ using the adjunction.

monadic

1. An adjunction is said to be monadic if it comes from the monad that it determines by means of the Eilenberg–Moore category (the category of algebras for the monad).2. A functor is said to be monadic if it is a constituent of a monadic adjunction.

monoidal category

A monoidal category, also called a tensor category, is a category C equipped with (1) a bifunctor ⊗ : C × C → C , (2) an identity object and (3) natural isomorphisms that make ⊗ associative and the identity object an identity for ⊗, subject to certain coherence conditions.

monoid object

A monoid object in a monoidal category is an object together with the multiplication map and the identity map that satisfy the expected conditions like associativity. For example, a monoid object in Set is a usual monoid (unital semigroup) and a monoid object in R-mod is an associative algebra over a commutative ring R.

monomorphism

A morphism f is a monomorphism (also called monic) if g = h whenever f ∘ g = f ∘ h ; e.g., an injection in Set. In other words, f is the dual of an epimorphism.

N

natural

1. A natural transformation is, roughly, a map between functors. Precisely, given a pair of functors F, G from a category C to category D, a natural transformation φ from F to G is a set of morphisms in D { ϕ x : F ( x ) → G ( x ) | x ∈ Ob ⁡ ( C ) } satisfying the condition: for each morphism f: x → y in C, ϕ y ∘ F ( f ) = G ( f ) ∘ ϕ x . For example, writing G L n ( R ) for the group of invertible n-by-n matrices with coefficients in a commutative ring R, we can view G L n as a functor from the category CRing of commutative rings to the category Grp of groups. Similarly, R ↦ R ∗ is a functor from CRing to Grp. Then the determinant det is a natural transformation from G L n to -^*.2. A natural isomorphism is a natural transformation that is an isomorphism (i.e., admits the inverse).

nerve

The nerve functor N is the functor from Cat to sSet given by N ( C ) n = Hom C a t ⁡ ( [ n ] , C ) .

normal

A category is normal if every monic is normal.

O

object

1. An object is part of a data defining a category.2. An [adjective] object in a category C is a contravariant functor (or presheaf) from some fixed category corresponding to the "adjective" to C. For example, a simplicial object in C is a contravariant functor from the simplicial category to C and a Γ-object is a pointed contravariant functor from Γ (roughly the pointed category of pointed finite sets) to C provided C is pointed.

op-fibration

A functor π:C → D is an op-fibration if, for each object x in C and each morphism g : π(x) → y in D, there is at least one π-coCartesian morphism f: x → y' in C such that π(f) = g. In other words, π is the dual of a Grothendieck fibration.

opposite

The opposite category of a category is obtained by reversing the arrows. For example, if a partially ordered set is viewed as a category, taking its opposite amounts to reversing the ordering.

P

perfect

Sometimes synonymous with "compact". See perfect complex.

pointed

A category (or ∞-category) is called pointed if it has a zero object.

polynomial

A functor from the category of finite-dimensional vector spaces to itself is called a polynomial functor if, for each pair of vector spaces V, W, F: Hom(V, W) → Hom(F(V), F(W)) is a polynomial map between the vector spaces. A Schur functor is a basic example.

preadditive

A category is preadditive if it is enriched over the monoidal category of abelian groups. More generally, it is R-linear if it is enriched over the monoidal category of R-modules, for R a commutative ring.

presentable

Given a regular cardinal κ, a category is κ-presentable if it admits all small colimits and is κ-accessible. A category is presentable if it is κ-presentable for some regular cardinal κ (hence presentable for any larger cardinal). Note: Some authors call a presentable category a locally presentable category.

presheaf

Another term for a contravariant functor: a functor from a category C^op to Set is a presheaf of sets on C and a functor from C^op to sSet is a presheaf of simplicial sets or simplicial presheaf, etc. A topology on C, if any, tells which presheaf is a sheaf (with respect to that topology).

product

1. The product of a family of objects X_i in a category C indexed by a set I is the projective limit lim ← of the functor I → C , i ↦ X i , where I is viewed as a discrete category. It is denoted by ∏ i X i and is the dual of the coproduct of the family.2. The product of a family of categories C_i's indexed by a set I is the category denoted by ∏ i C i whose class of objects is the product of the classes of objects of C_i's and whose hom-sets are ∏ i Hom C i ⁡ ( X i , Y i ) ; the morphisms are composed component-wise. It is the dual of the disjoint union.

projective

An object A in an abelian category is projective if the functor Hom ⁡ ( A , − ) is exact. It is the dual of an injective object.

Q

Quillen

Quillen’s theorem A provides a criterion for a functor to be a weak equivalence.

R

reflect

1. A functor is said to reflect identities if it has the property: if F(k) is an identity then k is an identity as well.2. A functor is said to reflect isomorphismsif it has the property: F(k) is an isomorphism then k is an isomorphism as well.

representable

A set-valued contravariant functor F on a category C is said to be representable if it belongs to the essential image of the Yoneda embedding C → F c t ( C op , S e t ) ; i.e., F ≃ Hom C ⁡ ( − , Z ) for some object Z. The object Z is said to be the representing object of F.

retraction

A morphism is a retraction if it has a right inverse.

S

section

A morphism is a section if it has a left inverse. For example, the axiom of choice says that any surjective function admits a section.

Segal space

Segal spaces were certain simplicial spaces, introduced as models for (∞, 1)-categories.

semisimple

An abelian category is semisimple if every short exact sequence splits. For example, a ring is semisimple if and only if the category of modules over it is semisimple.

Serre functor

Given a k-linear category C over a field k, a Serre functor f : C → C is an auto-equivalence such that Hom ⁡ ( A , B ) ≃ Hom ⁡ ( B , f ( A ) ) ∗ for any objects A, B.

simple

An object in an abelian category is simple if it is not isomorphic to the zero object and any subobject of A is isomorphic to zero or to A.

Simplicial localization

Simplicial localization is a method of localizing a category.

simplicial set

A simplicial set is a contravariant functor from Δ to Set, where Δ is the category whose objects are the sets [n] = { 0, 1, …, n } and whose morphisms are order-preserving functions. A morphism between simplicial sets is a natural transformation.

skeletal

A category is skeletal if isomorphic objects are necessarily identical.

slice

Given a category C and an object A in it, the slice category C_/A of C over A is the category whose objects are all the morphisms in C with codomain A, whose morphisms are morphisms in C such that if f is a morphism from p X : X → A to p Y : Y → A , then p Y ∘ f = p X in C and whose composition is that of C.

small

1. A small category is a category in which the class of all morphisms is a set (i.e., not a proper class); otherwise large. A category is locally small if the morphisms between every pair of objects A and B form a set. Some authors assume a foundation in which the collection of all classes forms a "conglomerate", in which case a quasicategory is a category whose objects and morphisms merely form a conglomerate. (NB: some authors use the term "quasicategory" with a different meaning.)2. An object in a category is said to be small if it is κ-compact for some regular cardinal κ. The notion prominently appears in Quiilen's small object argument (cf. https://ncatlab.org/nlab/show/small+object+argument)

stable

An ∞-category is stable if (1) it has a zero object, (2) every morphism in it admits a fiber and a cofiber and (3) a triangle in it is a fiber sequence if and only if it is a cofiber sequence.

strict

A morphism f in a category admitting finite limits and finite colimits is strict if the natural morphism Coim ⁡ ( f ) → Im ⁡ ( f ) is an isomorphism.

strict n-category

A strict 0-category is a set and for any integer n > 0, a strict n-category is a category enriched over strict (n-1)-categories. For example, a strict 1-category is an ordinary category. Note: the term "n-category" typically refers to "weak n-category"; not strict one.

subcanonical

A topology on a category is subcanonical if every representable contravariant functor on C is a sheaf with respect to that topology. Generally speaking, some flat topology may fail to be subcanonical; but flat topologies appearing in practice tend to be subcanonical.

subcategory

A category A is a subcategory of a category B if there is an inclusion functor from A to B.

subobject

Given an object A in a category, a subobject of A is an equivalence class of monomorphisms to A; two monomorphisms f, g are considered equivalent if f factors through g and g factors through f.

subquotient

A subquotient is a quotient of a subobject.

subterminal object

A subterminal object is an object X such that every object has at most one morphism into X.

symmetric monoidal category

A symmetric monoidal category is a monoidal category (i.e., a category with ⊗) that has maximally symmetric braiding.

T

t-structure

A t-structure is an additional structure on a triangulated category (more generally stable ∞-category) that axiomatizes the notions of complexes whose cohomology concentrated in non-negative degrees or non-positive degrees.

tensor category

Usually synonymous with monoidal category (though some authors distinguish between the two concepts.)

tensor triangulated category

A tensor triangulated category is a category that carries the structure of a symmetric monoidal category and of a triangulated category in a compatible way.

tensor product

Given a monoidal category B, the tensor product of functors F : C op → B and G : C → B is the coend: F ⊗ C G = ∫ c ∈ C F ( c ) ⊗ G ( c ) .

terminal

1. An object A is terminal (also called final) if there is exactly one morphism from each object to A; e.g., singletons in Set. It is the dual of an initial object.2. An object A in an ∞-category C is terminal if Map C ⁡ ( B , A ) is contractible for every object B in C.

thick subcategory

A full subcategory of an abelian category is thick if it is closed under extensions.

thin

A thin is a category where there is at most one morphism between any pair of objects.

triangulated category

A triangulated category is a category where one can talk about distinguished triangles, generalization of exact sequences. An abelian category is a prototypical example of a triangulated category. A derived category is a triangulated category that is not necessary an abelian category.

U

universal

1. Given a functor f : C → D and an object X in D, a universal morphism from X to f is an initial object in the comma category ( X ↓ f ) . (Its dual is also called a universal morphism.) For example, take f to be the forgetful functor V e c k → S e t and X a set. An initial object of ( X ↓ f ) is a function j : X → f ( V X ) . That it is initial means that if k : X → f ( W ) is another morphism, then there is a unique morphism from j to k, which consists of a linear map V X → W that extends k via j; that is to say, V X is the free vector space generated by X.2. Stated more explicitly, given f as above, a morphism X → f ( u X ) in D is universal if and only if the natural map Hom C ⁡ ( u X , c ) → Hom D ⁡ ( X , f ( c ) ) , α ↦ ( X → f ( u x ) → f ( α ) f ( c ) ) is bijective. In particular, if Hom C ⁡ ( u X , − ) ≃ Hom D ⁡ ( X , f ( − ) ) , then taking c to be u_X one gets a universal morphism by sending the identity morphism. In other words, having a universal morphism is equivalent to the representability of the functor Hom D ⁡ ( X , f ( − ) ) .

W

Waldhausen category

A Waldhausen category is, roughly, a category with families of cofibrations and weak equivalences.

wellpowered

A category is wellpowered if for each object there is only a set of pairwise non-isomorphic subobjects.

Y

Yoneda lemma

The Yoneda lemma says: For each set-valued contravariant functor F on C and an object X in C, there is a natural bijection F ( X ) ≃ Hom ⁡ ( Hom C ⁡ ( − , X ) , F ) ;

in particular, the functor

C → F c t ( C op , S e t ) , X ↦ Hom C ⁡ ( − , X )

is fully faithful.

Z

zero

A zero object is an object that is both initial and terminal, such as a trivial group in Grp.

References

Glossary of category theory Wikipedia

(Text) CC BY-SA

Contents

A

B

C

D

E

F

G

H

I

K

L

M

N

O

P

Q

R

S

T

U

W

Y

Z

References