 | ||
In mathematics, especially homotopy theory, the mapping cone is a construction
Contents
Definition
Given a map
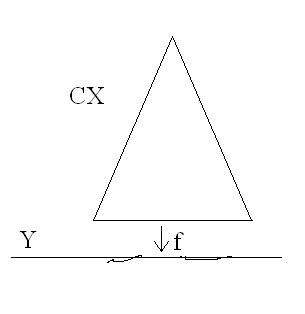
Visually, one takes the cone on X (the cylinder
Coarsely, one is taking the quotient space by the image of X, so Cf "=" Y/f(X); this is not precisely correct because of point-set issues, but is the philosophy, and is made precise by such results as the homology of a pair and the notion of an n-connected map.
The above is the definition for a map of unpointed spaces; for a map of pointed spaces
Example of circle
If
Consider, for example, the case where Y is the disc D2, and
f: S1 → Y = D2is the standard inclusion of the circle S1 as the boundary of D2. Then the mapping cone Cf is homeomorphic to two disks joined on their boundary, which is topologically the sphere S2.
Double mapping cylinder
The mapping cone is a special case of the double mapping cylinder. This is basically a cylinder joined on one end to a space X1 via the map
f1: S1 → X1and joined on the other end to a space X2 via the map
f2: S1 → X2.The mapping cone is the degenerate case of the double mapping cylinder (also known as the homotopy pushout), in which one space is a single point.
Dual construction: the mapping fibre
The dual to the mapping cone is the mapping fibre
Here, I is the unit interval and
It is dual to the mapping cone in the sense that the product above is essentially the fibered product or pullback
CW-complexes
Attaching a cell
Effect on fundamental group
Given a space X and a loop
representing an element of the fundamental group of X, we can form the mapping cone Cα. The effect of this is to make the loop α contractible in Cα, and therefore the equivalence class of α in the fundamental group of Cα will be simply the identity element.
Given a group presentation by generators and relations, one gets a 2-complex with that fundamental group.
Homology of a pair
The mapping cone lets one interpret the homology of a pair as the reduced homology of the quotient:
If E is a homology theory, and
Relation to homotopy (homology) equivalences
A map
More generally, a map is called n-connected (as a map) if its mapping cone is n-connected (as a space), plus a little more.
Let
Mapping cones are famously used to construct the long coexact Puppe sequences, from which long exact sequences of homotopy and relative homotopy groups can be obtained.
