Mapping cylinder

Basic properties

The bottom Y is a deformation retract of M f . The projection M f → Y splits (via Y ∋ y ↦ y ∈ Y ⊂ M f ), and a deformation retraction R is given by:

(where points in Y stay fixed, which is well-defined, because [ 0 , x ] = [ s ⋅ 0 , x ] for all s ).

The map f : X → Y is a homotopy equivalence if and only if the "top" { 1 } × X is a strong deformation retract of M f . An explicit formula for the strong deformation retraction can be worked out.

Interpretation

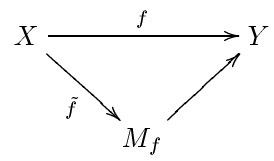
The mapping cylinder may be viewed as a way to replace an arbitrary map by an equivalent cofibration, in the following sense:

Given a map f : X → Y , the mapping cylinder is a space M f , together with a cofibration f ~ : X → M f and a surjective homotopy equivalence M f → Y (indeed, Y is a deformation retract of M f ), such that the composition X → M f → Y equals f.

Thus the space Y gets replaced with a homotopy equivalent space M f , and the map f with a lifted map f ~ . Equivalently, the diagram

gets replaced with a diagram

together with a homotopy equivalence between them.

The construction serves to replace any map of topological spaces by a homotopy equivalent cofibration.

Note that pointwise, a cofibration is a closed inclusion.

Applications

Mapping cylinders are quite common homotopical tools. One use of mapping cylinders is to apply theorems concerning inclusions of spaces to general maps, which might not be injective.

Consequently, theorems or techniques (such as homology, cohomology or homotopy theory) which are only dependent on the homotopy class of spaces and maps involved may be applied to f : X → Y with the assumption that X ⊂ Y and that f is actually the inclusion of a subspace.

Another, more intuitive appeal of the construction is that it accords with the usual mental image of a function as "sending" points of X to points of Y , and hence of embedding X within Y , despite the fact that the function need not be one-to-one.

Categorical application and interpretation

One can use the mapping cylinder to construct homotopy colimits: this follows from the general statement that any category with all pushouts and equalizers has all colimits. That is, given a diagram, replace the maps by cofibrations (using the mapping cylinder) and then take the ordinary pointwise limit (one must take a bit more care, but mapping cylinders are a component).

Conversely, the mapping cylinder is the homotopy pushout of the diagram where f : X → Y and id X : X → X .

Mapping telescope

Given a sequence of maps

the mapping telescope is the homotopical direct limit. If the maps are all already cofibrations (such as for the orthogonal groups O ( n ) ⊂ O ( n + 1 ) ), then the direct limit is the union, but in general one must use the mapping telescope. The mapping telescope is a sequence of mapping cylinders, joined end-to-end. The picture of the construction looks like a stack of increasingly large cylinders, like a telescope.

Formally, one defines it as