Harman Patil (Editor)

Cone (topology)

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Cone (topology)

In topology, especially algebraic topology, the cone CX of a topological space X is the quotient space:

Contents

C X = ( X × I ) / ( X × { 0 } )

of the product of X with the unit interval I = [0, 1]. Intuitively we make X into a cylinder and collapse one end of the cylinder to a point.

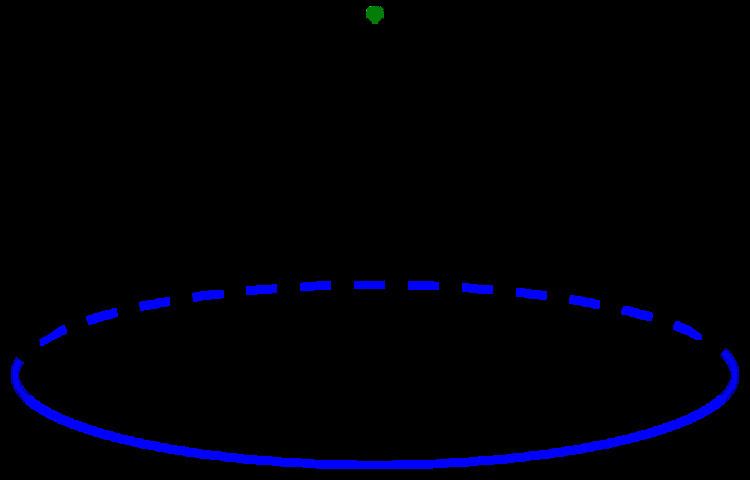
If X sits inside Euclidean space, the cone on X is homeomorphic to the union of lines from X to another point. That is, the topological cone agrees with the geometric cone when defined. However, the topological cone construction is more general.

Examples

  • The cone over a point p of the real line is the interval {p} x [0,1].
  • The cone over two points {0,1} is a "V" shape with endpoints at {0} and {1}.
  • The cone over an interval I of the real line is a filled-in triangle, otherwise known as a 2-simplex (see the final example).
  • The cone over a polygon P is a pyramid with base P.
  • The cone over a disk is the solid cone of classical geometry (hence the concept's name).
  • The cone over a circle is the curved surface of the solid cone:
    • This in turn is homeomorphic to the closed disc.
  • In general, the cone over an n-sphere is homeomorphic to the closed (n+1)-ball.
  • The cone over an n-simplex is an (n+1)-simplex.

    • Properties

    All cones are path-connected since every point can be connected to the vertex point. Furthermore, every cone is contractible to the vertex point by the homotopy

    ht(x,s) = (x, (1−t)s).

    The cone is used in algebraic topology precisely because it embeds a space as a subspace of a contractible space.

    When X is compact and Hausdorff (essentially, when X can be embedded in Euclidean space), then the cone CX can be visualized as the collection of lines joining every point of X to a single point. However, this picture fails when X is not compact or not Hausdorff, as generally the quotient topology on CX will be finer than the set of lines joining X to a point.

    Reduced cone

    If ( X , x 0 ) is a pointed space, there is a related construction, the reduced cone, given by

    X × [ 0 , 1 ] / ( X × { 0 } ∪ { x 0 } × [ 0 , 1 ] )

    With this definition, the natural inclusion x ↦ ( x , 1 ) becomes a based map, where we take ( x 0 , 0 ) to be the basepoint of the reduced cone.

    Cone functor

    The map X ↦ C X induces a functor C : T o p → T o p on the category of topological spaces Top.

    References

    Cone (topology) Wikipedia
    (Text) CC BY-SA


    Similar Topics