Homotopy lifting property - Alchetron, the free social encyclopedia

In mathematics, in particular in homotopy theory within algebraic topology, the homotopy lifting property (also known as the right lifting property or the covering homotopy axiom) is a technical condition on a continuous function from a topological space E to another one, B. It is designed to support the picture of E "above" B by allowing a homotopy taking place in B to be moved "upstairs" to E.

For example, a covering map has a property of unique local lifting of paths to a given sheet; the uniqueness is because the fibers of a covering map are discrete spaces. The homotopy lifting property will hold in many situations, such as the projection in a vector bundle, fiber bundle or fibration, where there need be no unique way of lifting.

Formal definition

Assume from now on all mappings are continuous functions from a topological space to another. Given a map π : E → B , and a space X , one says that ( X , π ) has the homotopy lifting property, or that π has the homotopy lifting property with respect to X , if:

for any homotopy f : X × [ 0 , 1 ] → B , and

for any map f ~ 0 : X → E lifting f 0 = f | X × { 0 } (i.e., so that f 0 = π ∘ f ~ 0 ),

there exists a homotopy f ~ : X × [ 0 , 1 ] → E lifting f (i.e., so that f = π ∘ f ~ ) which also satisfies f ~ 0 = f ~ | X × { 0 } .

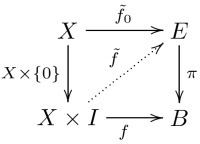
The following diagram depicts this situation.

The outer square (without the dotted arrow) commutes if and only if the hypotheses of the lifting property are true. A lifting f ~ corresponds to a dotted arrow making the diagram commute. This diagram is dual to that of the homotopy extension property; this duality is loosely referred to as Eckmann–Hilton duality.

If the map π satisfies the homotopy lifting property with respect to all spaces X, then π is called a fibration, or one sometimes simply says that π has the homotopy lifting property.

Note that this is the definition of fibration in the sense of Hurewicz, which is more restrictive than fibration in the sense of Serre, for which homotopy lifting only for X a CW complex is required.

Generalization: The Homotopy Lifting Extension Property

There is a common generalization of the homotopy lifting property and the homotopy extension property. Given a pair of spaces X ⊇ Y , for simplicity we denote T : = ( X × { 0 } ) ∪ ( Y × [ 0 , 1 ] ) ⊆ X × [ 0 , 1 ] . Given additionally a map π : E → B , one says that ( X , Y , π ) has the homotopy lifting extension property if:

For any homotopy f : X × [ 0 , 1 ] → B , and

For any lifting g ~ : T → E of g = f | T ,

there exists a homotopy f ~ : X × [ 0 , 1 ] → E which covers f (i.e., such that π f ~ = f ) and extends g ~ (i.e., such that f ~ | T = g ~ ).

The homotopy lifting property of ( X , π ) is obtained by taking Y = ∅ , so that T above is simply X × { 0 } .

The homotopy extension property of ( X , Y ) is obtained by taking π to be a constant map, so that π is irrelevant in that every map to E is trivially the lift of a constant map to the image point of π .

References

Homotopy lifting property Wikipedia

(Text) CC BY-SA

Contents

Formal definition

Generalization: The Homotopy Lifting Extension Property

References