 | ||
In complex analysis, a complex logarithm function is an "inverse" of the complex exponential function, just as the real natural logarithm ln x is the inverse of the real exponential function ex. Thus, a logarithm of a complex number z is a complex number w such that ew = z. The notation for such a w is ln z or log z. Since every nonzero complex number z has infinitely many logarithms, care is required to give such notation an unambiguous meaning.
Contents
- Problems with inverting the complex exponential function
- Definition of principal value
- Branches of the complex logarithm
- Branch cuts
- The derivative of the complex logarithm
- Constructing branches via integration
- The complex logarithm as a conformal map
- Construction
- The logarithm function on the Riemann surface
- Gluing all branches of logz
- The Riemann surface as a universal cover
- Applications
- Logarithms to other bases
- Logarithms of holomorphic functions
- References
If z = reiθ with r > 0 (polar form), then w = ln r + iθ is one logarithm of z; adding integer multiples of 2πi gives all the others.
Problems with inverting the complex exponential function
For a function to have an inverse, it must map distinct values to distinct values, i.e., be injective. But the complex exponential function is not injective, because ew+2πi = ew for any w, since adding iθ to w has the effect of rotating ew counterclockwise θ radians. Even worse, the infinitely many numbers
forming a sequence of equally spaced points along a vertical line, are all mapped to the same number by the exponential function. So the exponential function does not have an inverse function in the standard sense.
There are two solutions to this problem.
One is to restrict the domain of the exponential function to a region that does not contain any two numbers differing by an integer multiple of 2πi: this leads naturally to the definition of branches of log z, which are certain functions that single out one logarithm of each number in their domains. This is analogous to the definition of arcsin x on [−1, 1] as the inverse of the restriction of sin θ to the interval [−π/2, π/2]: there are infinitely many real numbers θ with sin θ = x, but one (somewhat arbitrarily) chooses the one in [−π/2, π/2].
Another way to resolve the indeterminacy is to view the logarithm as a function whose domain is not a region in the complex plane, but a Riemann surface that covers the punctured complex plane in an infinite-to-1 way.
Branches have the advantage that they can be evaluated at complex numbers. On the other hand, the function on the Riemann surface is elegant in that it packages together all branches of log z and does not require an arbitrary choice as part of its definition.
Definition of principal value
For each nonzero complex number z = x + yi, the principal value Log z is the logarithm whose imaginary part lies in the interval (−π,π]. The expression Log 0 is left undefined since there is no complex number w satisfying ew = 0.
The principal value can be described also in a few other ways.
To give a formula for Log z, begin by expressing z in polar form, z = reiθ. Given z, the polar form is not quite unique, because of the possibility of adding an integer multiple of 2π to θ, but it can be made unique by requiring θ to lie in the interval (−π,π]; this θ is called the principal value of the argument, and is sometimes written Arg z or (especially in computer languages) atan2(y,x), which agrees with arctan(y/x) when x > 0 but gives a correct value for any (x,y) ≠ (0,0). Then the principal value of the logarithm can be defined by
For example, Log(-3i) = ln 3 − πi/2.
Another way to describe Log z is as the inverse of a restriction of the complex exponential function, as in the previous section. The horizontal strip S consisting of complex numbers w = x+yi such that −π < y ≤ π is an example of a region not containing any two numbers differing by an integer multiple of 2πi, so the restriction of the exponential function to S has an inverse. In fact, the exponential function maps S bijectively to the punctured complex plane
When the notation log z appears without any particular logarithm having been specified, it is generally best to assume that the principal value is intended. In particular, this gives a value consistent with the real value of ln z when z is a positive real number. The capitalization in the notation Log is used by some authors to distinguish the principal value from other logarithms of z.
Not all identities satisfied by ln extend to complex numbers. It is true that eLog z = z for all z ≠ 0 (this is what it means for Log z to be a logarithm of z), but the identity Log ez = z fails for z outside the strip S. For this reason, one cannot always apply Log to both sides of an identity ez = ew to deduce z = w. Also, the identity Log(z1z2) = Log z1 + Log z2 can fail: the two sides can differ by an integer multiple of 2πi : for instance,
but
The function Log z is discontinuous at each negative real number, but continuous everywhere else in
Branches of the complex logarithm
Is there a different way to choose a logarithm of each nonzero complex number so as to make a function L(z) that is continuous on all of
To obtain a continuous logarithm defined on complex numbers, it is hence necessary to restrict the domain to a smaller subset U of the complex plane. Because one of the goals is to be able to differentiate the function, it is reasonable to assume that the function is defined on a neighborhood of each point of its domain; in other words, U should be an open set. Also, it is reasonable to assume that U is connected, since otherwise the function values on different components of U could be unrelated to each other. All this motivates the following definition:
For example, the principal value defines a branch on the open set where it is continuous, which is the set
Another example: The Mercator series
converges locally uniformly for |u| < 1, so setting z = 1+u defines a branch of log z on the open disk of radius 1 centered at 1. (Actually, this is just a restriction of Log z, as can be shown by differentiating the difference and comparing values at 1.)
Once a branch is fixed, it may be denoted "log z" if no confusion can result. Different branches can give different values for the logarithm of a particular complex number, however, so a branch must be fixed in advance (or else the principal branch must be understood) in order for "log z" to have a precise unambiguous meaning.
Branch cuts
The argument above involving the unit circle generalizes to show that no branch of log z exists on an open set U containing a closed curve that winds around 0. To foil this argument, U is typically chosen as the complement of a ray or curve in the complex plane going from 0 (inclusive) to infinity in some direction. In this case, the curve is known as a branch cut. For example, the principal branch has a branch cut along the negative real axis.
If the function L(z) is extended to be defined at a point of the branch cut, it will necessarily be discontinuous there; at best it will be continuous "on one side", like Log z at a negative real number.
The derivative of the complex logarithm
Each branch L(z) of log z on an open set U is an inverse of a restriction of the exponential function, namely the restriction to the image of U under L. Since the exponential function is holomorphic (i.e., complex differentiable) with nonvanishing derivative, the complex analogue of the inverse function theorem applies. It shows that L(z) is holomorphic at each z in U, and L′(z) = 1/z. Another way to prove this is to check the Cauchy-Riemann equations in polar coordinates.
Constructing branches via integration
The function
If the range of integration started at a positive number a other than 1, the formula would have to be
instead.
In developing the analogue for the complex logarithm, there is an additional complication: the definition of the complex integral requires a choice of path. Fortunately, if the integrand is holomorphic, then the value of the integral is unchanged by deforming the path (while holding the endpoints fixed), and in a simply connected region U (a region with "no holes") any path from a to z inside U can be continuously deformed inside U into any other. All this leads to the following:
The complex logarithm as a conformal map
Any holomorphic map
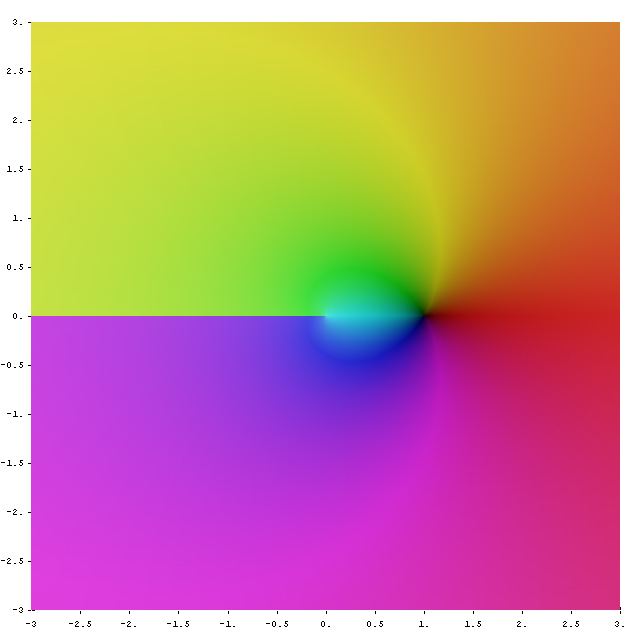
For example, the principal branch w = Log z, viewed as a mapping from
Each circle and ray in the z-plane as above meet at a right angle. Their images under Log are a vertical segment and a horizontal line (respectively) in the w-plane, and these too meet at a right angle. This is an illustration of the conformal property of Log.
Construction
The various branches of log z cannot be glued to give a single function
One can continue by gluing branches with imaginary part θ in (π,3π), in (2π,4π), and so on, and in the other direction, branches with imaginary part θ in (−2π,0), in (−3π,−π), and so on. The final result is a connected surface that can be viewed as a spiralling parking garage with infinitely many levels extending both upward and downward. This is the Riemann surface R associated to log z.
A point on R can be thought of as a pair (z,θ) where θ is a possible value of the argument of z. In this way, R can be embedded in
The logarithm function on the Riemann surface
Because the domains of the branches were glued only along open sets where their values agreed, the branches glue to give a single well-defined function
There is a "projection map" from R down to
Gluing all branches of log z
Instead of gluing only the branches chosen above, one can start with all branches of log z, and simultaneously glue every pair of branches
If U′ is an open subset of R projecting bijectively to its image U in
The Riemann surface as a universal cover
The projection map
As a complex manifold, R is biholomorphic with
Applications
Logarithms to other bases
Just as for real numbers, one can define for complex numbers a and b
the only caveat being that its value depends on the choice of a branch of log defined at a and b (with log a ≠ 0). For example, using the principal value gives
Logarithms of holomorphic functions
If f is a holomorphic function on a connected open subset U of
If U is a simply connected open subset of
for each z in U.
