 | ||
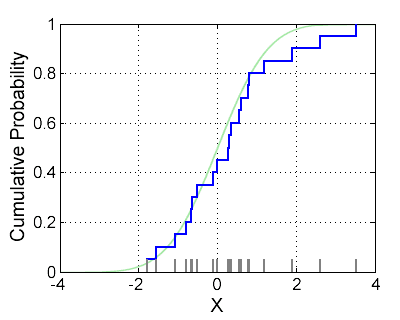
In statistics, an empirical distribution function is the distribution function associated with the empirical measure of a sample. This cumulative distribution function is a step function that jumps up by 1/n at each of the n data points. Its value at any specified value of the measured variable is the fraction of observations of the measured variable that are less than or equal to the specified value.
Contents
The empirical distribution function estimates the cumulative distribution function underlying of the points in the sample and converges with probability 1 according to the Glivenko–Cantelli theorem. A number of results exist to quantify the rate of convergence of the empirical distribution function to the underlying cumulative distribution function.
Definition
Let (x1, …, xn) be independent, identically distributed real random variables with the common cumulative distribution function F(t). Then the empirical distribution function is defined as
where
However, in some textbooks, the definition is given as
Asymptotic properties
Since the ratio (n+1) / n approaches 1 as n goes to infinity, the asymptotic properties of the two definitions that are given above are the same.
By the strong law of large numbers, the estimator
thus the estimator
The sup-norm in this expression is called the Kolmogorov–Smirnov statistic for testing the goodness-of-fit between the empirical distribution
The asymptotic distribution can be further characterized in several different ways. First, the central limit theorem states that pointwise,
This result is extended by the Donsker’s theorem, which asserts that the empirical process
The uniform rate of convergence in Donsker’s theorem can be quantified by the result known as the Hungarian embedding:
Alternatively, the rate of convergence of
In fact, Kolmogorov has shown that if the cumulative distribution function F is continuous, then the expression
Another result, which follows from the law of the iterated logarithm, is that
and
