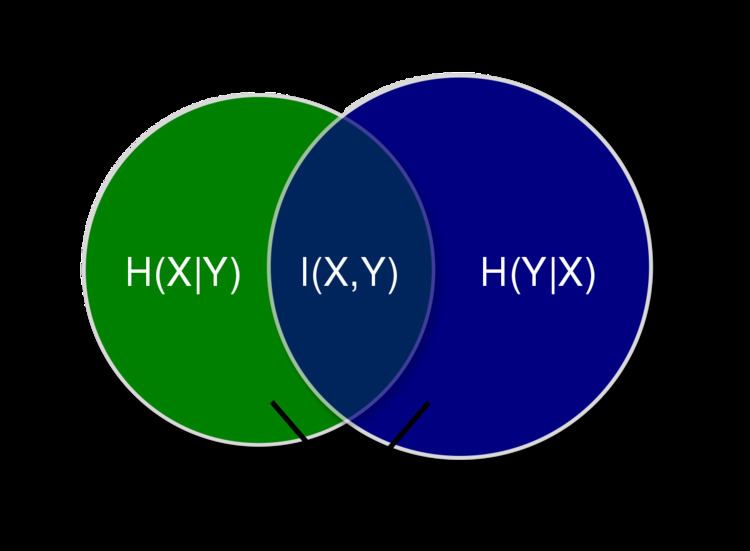
Variation of information - Alchetron, the free social encyclopedia

In probability theory and information theory, the variation of information or shared information distance is a measure of the distance between two clusterings (partitions of elements). It is closely related to mutual information; indeed, it is a simple linear expression involving the mutual information. Unlike the mutual information, however, the variation of information is a true metric, in that it obeys the triangle inequality.

Definition

Suppose we have two partitions X and Y of a set A into disjoint subsets, namely X = { X 1 , X 2 , . . , , X k } , Y = { Y 1 , Y 2 , . . , , Y l } . Let n = ∑ i | X i | + ∑ j | Y j | = | A | , p i = | X i | / n , q j = | Y j | / n , r i j = | X i ∩ Y j | / n . Then the variation of information between the two partitions is:

V I ( X ; Y ) = − ∑ i , j r i j [ log ⁡ ( r i j / p i ) + log ⁡ ( r i j / q j ) ] .

This is equivalent to the shared information distance between the random variables i and j with respect to the uniform probability measure on A defined by μ ( B ) := | B | / n for B ⊆ A .

Identities

The variation of information satisfies

V I ( X ; Y ) = H ( X ) + H ( Y ) − 2 I ( X , Y ) ,

where H ( X ) is the entropy of X , and I ( X , Y ) is mutual information between X and Y with respect to the uniform probability measure on A . This can be rewritten as

V I ( X ; Y ) = H ( X , Y ) − I ( X , Y ) ,

where H ( X , Y ) is the joint entropy of X and Y , or

V I ( X ; Y ) = H ( X | Y ) + H ( Y | X ) ,

where H ( X | Y ) and H ( Y | X ) are the respective conditional entropies.

References

Variation of information Wikipedia

(Text) CC BY-SA

Contents

Definition

Identities

References