Van Hove singularity

Theory

Consider a one-dimensional lattice of N particle sites, with each particle site separated by distance a, for a total length of L = Na. Instead of assuming that the waves in this one-dimensional box are standing waves, it is more convenient to adopt periodic boundary conditions:

where λ is wavelength, and n is an integer. (Positive integers will denote forward waves, negative integers will denote reverse waves.) The shortest wavelength needed to describe a wavemotion in the lattice is equal to 2a which then corresponds to the largest needed wave number k m a x = π / a and which also corresponds to the maximum possible |n|: n m a x = L / 2 a . We may define the density of states g(k)dk as the number of standing waves with wave vector k to k+dk:

Extending the analysis to wavevectors in three dimensions the density of states in a box will be

where d 3 k is a volume element in k-space, and which, for electrons, will need to be multiplied by a factor of 2 to account for the two possible spin orientations. By the chain rule, the DOS in energy space can be expressed as

where ∇ → is the gradient in k-space.

The set of points in k-space which correspond to a particular energy E form a surface in k-space, and the gradient of E will be a vector perpendicular to this surface at every point. The density of states as a function of this energy E is:

where the integral is over the surface ∂ E of constant E. We can choose a new coordinate system k x ′ , k y ′ , k z ′ such that k z ′ is perpendicular to the surface and therefore parallel to the gradient of E. If the coordinate system is just a rotation of the original coordinate system, then the volume element in k-prime space will be

We can then write dE as:

and, substituting into the expression for g(E) we have:

where the d k x ′ d k y ′ term is an area element on the constant-E surface. The clear implication of the equation for g ( E ) is that at the k -points where the dispersion relation E ( k → ) has an extremum, the integrand in the DOS expression diverges. The Van Hove singularities are the features that occur in the DOS function at these k -points.

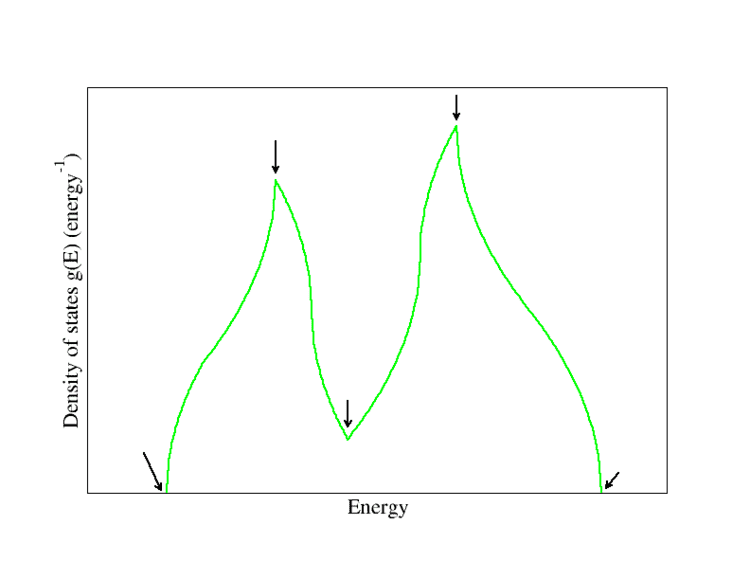
A detailed analysis shows that there are four types of Van Hove singularities in three-dimensional space, depending on whether the band structure goes through a local maximum, a local minimum or a saddle point. In three dimensions, the DOS itself is not divergent although its derivative is. The function g(E) tends to have square-root singularities (see the Figure) since for a spherical free electron Fermi surface

In two dimensions the DOS is logarithmically divergent at a saddle point and in one dimension the DOS itself is infinite where ∇ → E is zero.

Experimental observation

The optical absorption spectrum of a solid is most straightforwardly calculated from the electronic band structure using Fermi's Golden Rule where the relevant matrix element to be evaluated is the dipole operator A → ⋅ p → where A → is the vector potential and p → is the momentum operator. The density of states which appears in the Fermi's Golden Rule expression is then the joint density of states, which is the number of electronic states in the conduction and valence bands that are separated by a given photon energy. The optical absorption is then essentially the product of the dipole operator matrix element (also known as the oscillator strength) and the JDOS.

The divergences in the two- and one-dimensional DOS might be expected to be a mathematical formality, but in fact they are readily observable. Highly anisotropic solids like graphite (quasi-2D) and Bechgaard salts (quasi-1D) show anomalies in spectroscopic measurements that are attributable to the Van Hove singularities. Van Hove singularities play a significant role in understanding optical intensities in single-walled carbon nanotubes (SWNTs) which are also quasi-1D systems. The Dirac point in graphene is a Van-Hove singularity that can be seen directly as a peak in electrical resistance, when the graphene is charge-neutral. Twisted graphene layers also show pronounced Van-Hove singularities in the DOS due to the interlayer coupling.