 | ||
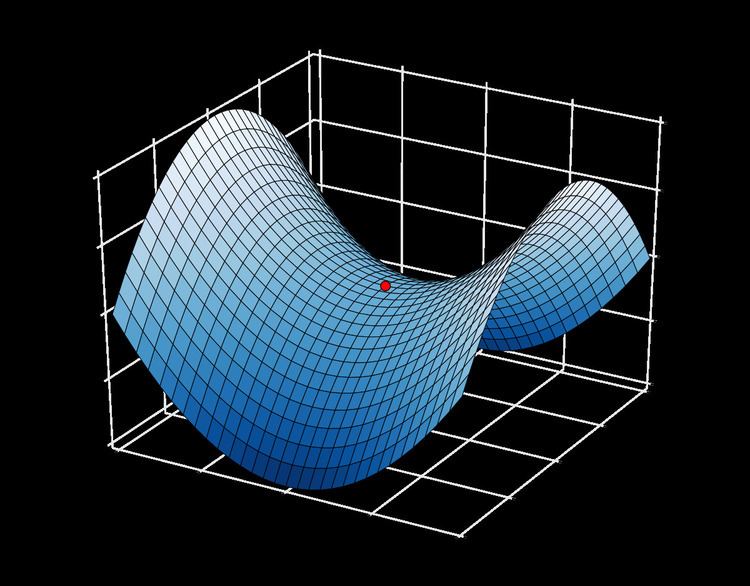
In mathematics, a saddle point or minimax point is a point in the domain of a function where the slopes (derivatives) of orthogonal function components defining the surface become zero (a stationary point) but are not a local extremum on both axes. The saddle point will always occur at a relative minimum along one axial direction (between peaks) and where the crossing axis is a relative maximum.
Contents
The name derives from the fact that the prototypical example in two dimensions is a surface that curves up in one direction, and curves down in a different direction, resembling a riding saddle or a mountain pass between two peaks forming a landform saddle. In terms of contour lines, a saddle point in two dimensions gives rise to a contour graph or trace that appears to intersect itself—such conceptually might form a 'figure eight' around both peaks; assuming the contour graph is at the very 'specific altitude' of the saddle point in three dimensions.
Mathematical discussion
A simple criterion for checking if a given stationary point of a real-valued function F(x,y) of two real variables is a saddle point is to compute the function's Hessian matrix at that point: if the Hessian is indefinite, then that point is a saddle point. For example, the Hessian matrix of the function
which is indefinite. Therefore, this point is a saddle point. This criterion gives only a sufficient condition. For example, the point
In the most general terms, a saddle point for a smooth function (whose graph is a curve, surface or hypersurface) is a stationary point such that the curve/surface/etc. in the neighborhood of that point is not entirely on any side of the tangent space at that point.
In one dimension, a saddle point is a point which is both a stationary point and a point of inflection. Since it is a point of inflection, it is not a local extremum.
Saddle surface
A saddle surface is a smooth surface containing one or more saddle points.
Classical examples of two-dimensional saddle surfaces in the Euclidean space are second order surfaces, the hyperbolic paraboloid
Saddle surfaces have negative Gaussian curvature which distinguish them from convex/elliptical surfaces which have positive Gaussian curvature. A classical third-order saddle surface is the monkey saddle.
Other uses
In dynamical systems, if the dynamic is given by a differentiable map f then a point is hyperbolic if and only if the differential of ƒ n (where n is the period of the point) has no eigenvalue on the (complex) unit circle when computed at the point. Then a saddle point is a hyperbolic periodic point whose stable and unstable manifolds have a dimension that is not zero.
In a two-player zero sum game defined on a continuous space, the equilibrium point is a saddle point.
A saddle point of a matrix is an element which is both the largest element in its column and the smallest element in its row.
For a second-order linear autonomous system, a critical point is a saddle point if the characteristic equation has one positive and one negative real eigenvalue.
