Translation operator (quantum mechanics)

Action on position eigenkets and wavefunctions

The translation operator T ^ ( x ) moves particles and fields by the amount x. Therefore, if a particle is in an eigenstate of the position operator | r ⟩ (i.e., precisely located at the position r), then after T ^ ( x ) acts on it, the particle is at the position (r+x):

An alternative (and equivalent) way to describe what the translation operator does is based on position-space wavefunctions. If a particle has a position-space wavefunction ψ ( r ) , and T ^ ( x ) acts on the particle, the new position-space wavefunction is ψ ′ ( r ) defined by ψ ′ ( r ) = ψ ( r − x ) . This relation is easier to remember as ψ ′ ( r + x ) = ψ ( r ) : "The value of the new wavefunction at the new point equals the value of the old wavefunction at the old point".

Here is an example showing that these two descriptions are equivalent. The state | a ⟩ corresponds to the wavefunction ψ ( r ) = δ ( r − a ) (where δ is the Dirac delta function), while the state T ^ ( x ) | a ⟩ = | a + x ⟩ corresponds to the wavefunction ψ ′ ( r ) = δ ( r − ( a + x ) ) . These indeed satisfy ψ ′ ( r ) = ψ ( r − x ) .

Momentum as generator of translations

In introductory physics, momentum is usually defined as mass times velocity. However, there is a more fundamental way to define momentum, in terms of translation operators. This is more specifically called canonical momentum, and it is usually but not always equal to mass times velocity; one counterexample is a charged particle in a magnetic field. This definition of momentum is especially important because the law of conservation of momentum applies only to canonical momentum, and is not universally valid if momentum is defined instead as mass times velocity (the so-called "kinetic momentum"), for reasons explained below.

The (canonical) momentum operator is defined as the gradient of the translation operators near the origin:

where ħ is reduced Planck's constant. For example, what is the result when the p ^ x operator acts on a quantum state? To find the answer, translate the state by an infinitesimal amount in the x-direction, and calculate the rate that the state is changing, and multiply it by iħ. For example, if a state does not change at all when it is translated in the x-direction, then its x component of momentum is 0.

More explicitly, p ^ is a vector operator (i.e. a vector consisting of three operators ( p ^ x , p ^ y , p ^ z ) ), defined by:

where ħ is reduced Planck's constant, I ^ is the identity operator and x ^ is the unit vector in the x-direction. ( p ^ y , p ^ z are defined analogously.)

The equation above is the most general definition of p ^ . In the special case of a single particle with wavefunction ψ ( r ) , p ^ can be written in a more specific and useful form. In one dimension:

or in three dimensions,

as an operator acting on position-space wavefunctions. This is the familiar quantum-mechanical expression for p ^ , but we have derived it here from a more basic starting point.

We have now defined p ^ in terms of translation operators. It is also possible to write a translation operator as a function of p ^ . The method is: First, express a given translation as a huge number N of consecutive tiny translations, and then use the fact that infinitesimal translations can be written in terms of p ^ :

which gives the final expression:

where exp is operator exponential and the right-hand side is the Taylor series expansion. For very small x, one can use the approximation:

Hence, momentum operator is referred to as the generator of translation.

A nice way to double-check that these relations are correct is to do Taylor expansion of a translation operator acting on a position-space wavefunction. Expanding the exponential to all orders, the translation operator generates exactly the full Taylor expansion of a test function:

So every translation operator generates exactly the expected translation on a test function if the function is analytic in some domain of the complex plane.

Successive translations

In other words, if you move particles and fields by the amount x₁, then you move them by the amount x₂, then overall you have moved them by the amount x₁ + x₂. For a mathematical proof, one can look at what these operators do to a particle in a position eigenstate:

Since the operators T ^ ( x 1 ) T ^ ( x 2 ) and T ^ ( x 1 + x 2 ) have the same effect on every state in an eigenbasis, it follows that the operators are equal.

Inverse

The translation operators are invertible, and their inverses are:

This follows from the "successive translations" property above, and the fact that T ^ ( 0 ) = I ^ , i.e. a translation by a distance of 0 is the same as the identity operator which leaves all states unchanged.

Translation operators commute with each other

because both sides are equal to T ^ ( x + y ) .

Translation operators are unitary

If ψ ( r ) and ϕ ( r ) are two position-space wavefunctions, then the inner product of ψ with ϕ is:

while the inner product of T ^ ( a ) ψ with T ^ ( a ) ϕ is:

By change of variables, these two inner products are exactly the same. Therefore the translation operators are unitary, and in particular:

The fact that translation operators are unitary implies that the momentum operator is Hermitian.

Translation operating on a bra

A translation operator operating on a bra in the position eigenbasis gives:

Splitting a translation into its components

According to the "successive translations" property above, a translation by the vector x = ( x , y , z ) can be written as the product of translations in the component directions:

where x ^ , y ^ , z ^ are unit vectors.

Commutator with position operator

Suppose | r ⟩ is an eigenvector of the position operator r ^ with eigenvalue r . We have

while

Therefore the commutator between a translation operator and the position operator is:

This can also be written (using the above properties) as:

where I ^ is the identity operator.

Commutator with momentum operator

Since translation operators commute with each other, and since the momentum operator is a sum of scaled infinitesimal translation operators, it follows that translation operators all commute with the momentum operator, i.e.

The translation group

The set T of translation operators T ^ ( x ) for all x , with the operation of multiplication defined as the result of successive translations (i.e. function composition), satisfies all the axioms of a group:

Therefore the set T of translation operators T ^ ( x ) for all x forms a group. Since there are continuously infinite number of elements, the translation group is a continuous group. Moreover, the translation operators commute among themselves, i.e. the product of two translation (a translation followed by another) does not depend on their order. Therefore, the translation group is an abelian group.

The translation group acting on the Hilbert space of position eigenstates is isomorphic to the group of vector additions in the Euclidean space.

Expectation values of position and momentum in the translated state

Consider a single particle in one dimension. Unlike classical mechanics, in quantum mechanics, a particle neither has a well defined position nor a well defined momentum. In the quantum formulation the expectation values play the role of the classical variables. For example, if a particle is in state | ψ ⟩ , then the expectation value of position is ⟨ ψ | r ^ | ψ ⟩ , where r ^ is the position operator.

If a translation operator T ^ ( x ) acts on the state | ψ ⟩ , creating a new state | ψ 2 ⟩ then the expectation value of position for | ψ 2 ⟩ is equal to the expectation value of position for | ψ ⟩ plus the vector x. This result is consistent with what you would expect from an operation that shifts the particle by that amount.

On the other hand, when the translation operator acts on a state, the expectation value of momentum is not changed. This can be proven in a similar way as the above, but using the fact that translation operators commute with the momentum operator. This result is again consistent with expectations: Translating a particle does not change its velocity or mass, so its momentum should not change.

Translational Invariance

In quantum mechanics, the Hamiltonian represents the energy and dynamics of a system. In some circumstances described below, the Hamiltonian is not changed if a system is translated. In that case, we say the corresponding translation operator is a symmetry of the system. Mathematically, this situation occurs when:

(loosely speaking, if we translate the system, then measure its energy, then translate it back, it amounts to the same thing as just measuring its energy directly). This can also be written as a commutator [ H ^ , T ^ ( x ) ] = 0 , i.e. the Hamiltonian commutes with the translation operator.

Continuous Translational Symmetry

First we consider the case where all the translation operators are symmetries of the system. As we will see, in this case conservation of momentum occurs.

For example, if H is the Hamiltonian describing all particles and fields in the universe, and T ^ ( x ) is the translation operator that shifts all particles and fields in the universe simultaneously by the same amount, then this is always a symmetry: H describes the complete laws of physics in our universe, which are independent of location. As a consequence, conservation of momentum is universally valid.

On the other hand, perhaps H and T ^ ( x ) refer to just one particle. Then the translation operators T ^ ( x ) are exact symmetries only if the particle is alone in a vacuum. Correspondingly, the momentum of a single particle is not usually conserved (it changes when the particle bumps into other objects), but it is conserved if the particle is alone in a vacuum.

The connection to conservation of momentum comes from the following argument. Assume that all the translation operators are symmetries of the system (i.e., the Hamiltonian H commutes with all of them). Then H must also commute with the momentum operator, since the momentum operator can be written as a sum of scaled infinitesimal translation operators.

It now follows from the Ehrenfest theorem (since momentum operator p ^ is time independent) that:

In summary, whenever the Hamiltonian for a system remains invariant under continuous translation, then the system has conservation of momentum, meaning that the expectation value of the momentum operator remains constant. This is an example of Noether's theorem.

Discrete Translational Symmetry

There is another special case where the Hamiltonian may be translationally invariant. This type of translational symmetry is observed whenever the potential is periodic.

In general, the Hamiltonian is not invariant under any translation represented by T ^ j ( x j ) with x j arbitrary, where T ^ j ( x j ) has the property:

and,

(where I ^ is the identity operator; see proof above).

But, whenever x j coincides with the period of the potential a ,

Since the kinetic energy part of the Hamiltonian H ^ being function of p ^ is already invariant under any arbitrary translation, the entire Hamiltonian satisfies,

Now, the Hamiltonian commutes with translation operator, i.e. they can be simultaneously diagonalised. Therefore the Hamiltonian is invariant under such translation (which no longer remains continuous). The translation becomes discrete with the period of the potential.

Discrete Translation in Periodic Potential: Bloch's Theorem

The ions in a perfect crystal are arranged in a regular periodic array. So we are led to the problem of an electron in a potential V ( r ) with the periodicity of the underlying Bravais lattice

for all Bravais lattice vectors R

However, perfect periodicity is an idealisation. Real solids are never absolutely pure, and in the neighbourhood of the impurity atoms the solid is not the same as elsewhere in the crystal. Moreover, the ions are not in fact stationary, but continually undergo thermal vibrations about their equilibrium positions. These destroy the perfect translational symmetry of a crystal. To deal with this type of problems the main problem is artificially divided in two parts: (a) the ideal fictitious perfect crystal, in which the potential is genuinely periodic, and (b) the effects on the properties of a hypothetical perfect crystal of all deviations from perfect periodicity, treated as small perturbations.

Although, the problem of electrons in a solid is in principle a many-electron problem, in independent electron approximation each of the electron is subjected to one electron Schrödinger equation with a periodic potential and are known as "Bloch electron" (in contrast to free electrons, to which Bloch electrons reduce when the periodic potential is identically zero.)

For each Bravais lattice vector R we define a translation operator T ^ R which, when operating on any function f ( r ) shifts the argument by R :

Since all translations form an Abelian group, the result of applying two successive translations does not depend on the order in which they are applied, i.e.

In addition, as the Hamiltonian is periodic, we have,

Hence, the T ^ R for all Bravais lattice vectors R and the Hamiltonian H ^ form a set of commutating operators. Therefore the eigenstates of H ^ can be chosen to be simultaneous eigenstates of all the T ^ R :

The eigenvalues c ( R ) of the translation operators are related because of the condition:

We have,

And,

Therefore, it follows that,

Now let a i be the three primitive vector for the Bravais lattice. By a suitable choice of x i , we can always write c ( a i ) in the form

Now if R is a general Bravais lattice vector, given by

it follows then,

Substituting c ( a i ) = e 2 π i x i one gets,

where k = b 1 x 1 + b 2 x 2 + b 3 x 3 and b i 's are the reciprocal lattice vectors satisfying the equation b i ⋅ a j = 2 π δ i j

Therefore one can choose the simultaneous eigenstates ψ of the Hamiltonian H ^ and T ^ R so that for every Bravais lattice vector R ,

So,

This result is known as Bloch Theorem

Time Evolution and Translational Invariance

In the passive transformation picture, translational invariance requires,

It follows that

where U ^ ( t ) is the Unitary Time Evolution operator. When the Hamiltonian is time independent,

If the Hamiltonian is time dependent, the above commutation relation is satisfied if p ^ or T ^ ( x ) commutes with H ^ ( t ) for all t.

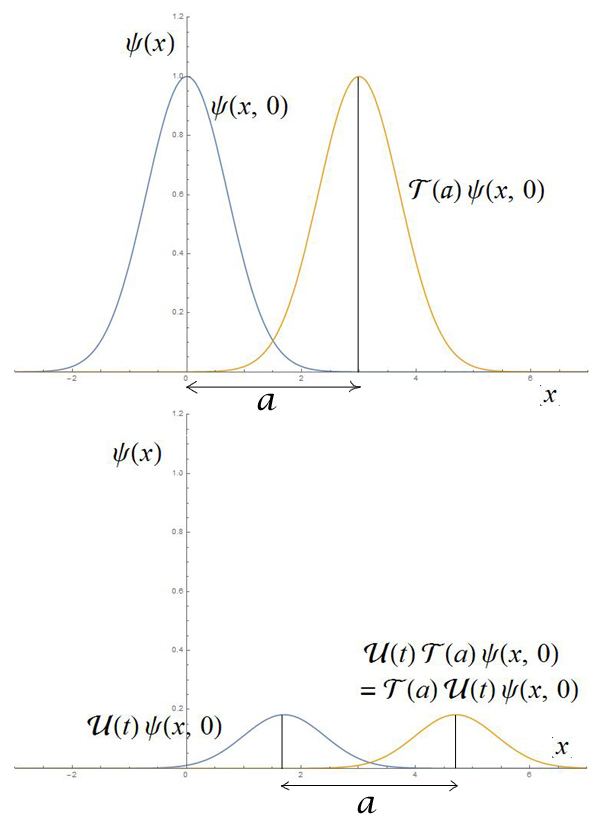
Example

Suppose at t = 0 two observers A and B prepare identical systems at x = 0 and x = a (fig. 1), respectively.If | ψ ( 0 ) ⟩ be the state vector of the system prepared by A, then the state vector of the system prepared by B wil be given by

Both the systems look identical to the observers who prepared them. After time t , the state vectors evolve into U ^ ( t ) | ψ ( 0 ) ⟩ and U ^ ( t ) T ^ ( a ) | ψ ( 0 ) ⟩ respectively. Using the above mentioned commutation relation, the later may be written as,

which is just the translated version of the system preapred by A at time t. Therefore, the two systems, which differed only by a translation at t = 0 , differ only by the same translation at any instant of time. The time evolution of both the systems appear the same to the observers who prepared them. It can be concluded that the translational invariance of Hamiltonian implies that the same experiment repeated at two different places will give the same result (as seen by the local observers).