Information theory and measure theory

Measures in information theory

Many of the concepts in information theory have separate definitions and formulas for continuous and discrete cases. For example, entropy H ( X ) is usually defined for discrete random variables, whereas for continuous random variables the related concept of differential entropy, written h ( X ) , is used (see Cover and Thomas, 2006, chapter 8). Both these concepts are mathematical expectations, but the expectation is defined with an integral for the continuous case, and a sum for the discrete case.

These separate definitions can be more closely related in terms of measure theory. For discrete random variables, probability mass functions can be considered density functions with respect to the counting measure. Thinking of both the integral and the sum as integration on a measure space allows for a unified treatment.

Consider the formula for the differential entropy of a continuous random variable X with range R and probability density function f ( x ) :

This can usually be interpreted as the following Riemann–Stieltjes integral:

where μ is the Lebesgue measure.

If instead, X is discrete, with range Ω a finite set, f is a probability mass function on Ω , and ν is the counting measure on Ω , we can write:

The integral expression, and the general concept, are identical in the continuous case; the only difference is the measure used. In both cases the probability density function f is the Radon–Nikodym derivative of the probability measure with respect to the measure against which the integral is taken.

If P is the probability measure on X , then the integral can also be taken directly with respect to P :

If instead of the underlying measure μ we take another probability measure Q , we are led to the Kullback–Leibler divergence: let P and Q be probability measures over the same space. Then if P is absolutely continuous with respect to Q , written P ≪ Q , the Radon–Nikodym derivative d P d Q exists and the Kullback–Leibler divergence can be expressed in its full generality:

where the integral runs over the support of P . Note that we have dropped the negative sign: the Kullback–Leibler divergence is always non-negative due to Gibbs' inequality.

Entropy as a "measure"

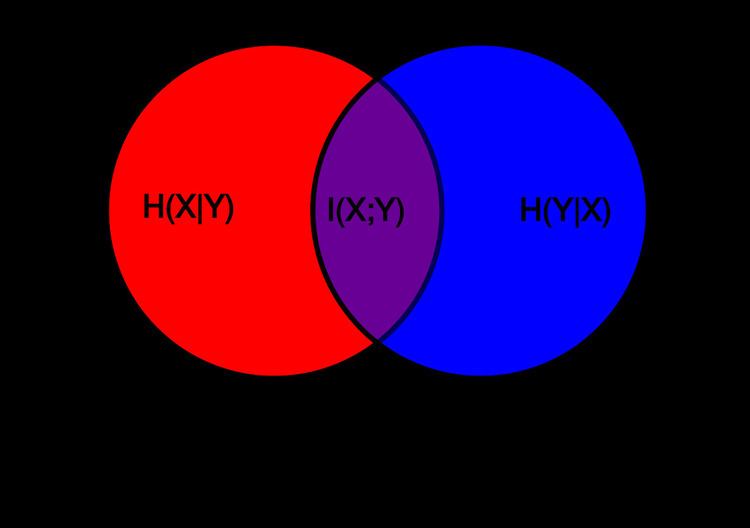
There is an analogy between Shannon's basic "measures" of the information content of random variables and a measure over sets. Namely the joint entropy, conditional entropy, and mutual information can be considered as the measure of a set union, set difference, and set intersection, respectively (Reza pp. 106–108).

If we associate the existence of abstract sets X ~ and Y ~ to arbitrary discrete random variables X and Y, somehow representing the information borne by X and Y, respectively, such that:

where μ is a signed measure over these sets, and we set:

we find that Shannon's "measure" of information content satisfies all the postulates and basic properties of a formal signed measure over sets, as commonly illustrated in an information diagram. This allows the sum of two measures to be written:

and the analog of Bayes' theorem ( μ ( A ) + μ ( B ∖ A ) = μ ( B ) + μ ( A ∖ B ) ) allows the difference of two measures to be written:

This can be a handy mnemonic device in some situations, e.g.

Note that measures (expectation values of the logarithm) of true probabilities are called "entropy" and generally represented by the letter H, while other measures are often referred to as "information" or "correlation" and generally represented by the letter I. For notational simplicity, the letter I is sometimes used for all measures.

Multivariate mutual information

Certain extensions to the definitions of Shannon's basic measures of information are necessary to deal with the σ-algebra generated by the sets that would be associated to three or more arbitrary random variables. (See Reza pp. 106–108 for an informal but rather complete discussion.) Namely H ( X , Y , Z , ⋯ ) needs to be defined in the obvious way as the entropy of a joint distribution, and a multivariate mutual information I ( X ; Y ; Z ; ⋯ ) defined in a suitable manner so that we can set:

in order to define the (signed) measure over the whole σ-algebra. There is no single universally accepted definition for the mutivariate mutual information, but the one that corresponds here to the measure of a set intersection is due to Fano (Srinivasa). The definition is recursive. As a base case the mutual information of a single random variable is defined to be its entropy: I ( X ) = H ( X ) . Then for n ≥ 2 we set

where the conditional mutual information is defined as

The first step in the recursion yields Shannon's definition I ( X 1 ; X 2 ) = H ( X 1 ) − H ( X 1 ∣ X 2 ) . It is interesting to note that the multivariate mutual information (same as interaction information but for a change in sign) of three or more random variables can be negative as well as positive: Let X and Y be two independent fair coin flips, and let Z be their exclusive or. Then I ( X ; Y ; Z ) = − 1 bit.

Many other variations are possible for three or more random variables: for example, I ( X , Y ; Z ) is the mutual information of the joint distribution of X and Y relative to Z, and can be interpreted as μ ( ( X ~ ∪ Y ~ ) ∩ Z ~ ) . Many more complicated expressions can be built this way, and still have meaning, e.g. I ( X , Y ; Z ∣ W ) , or H ( X , Z ∣ W , Y ) .