 | ||
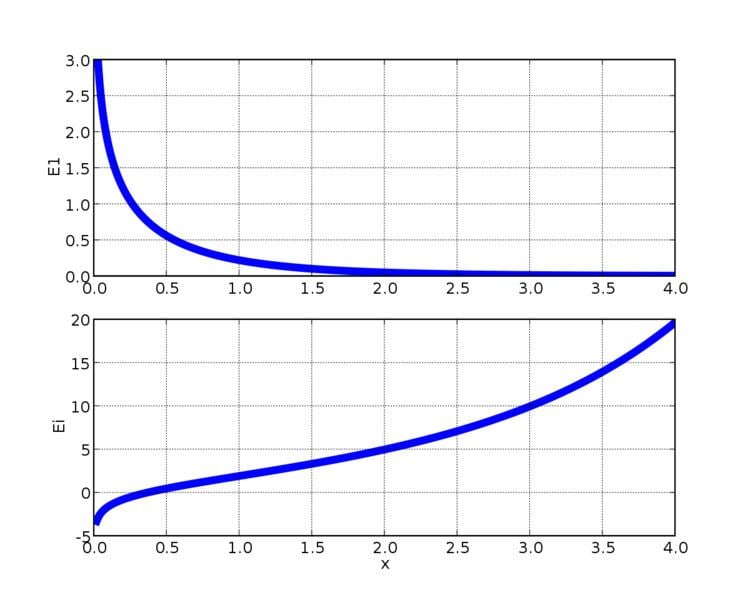
In mathematics, the exponential integral Ei is a special function on the complex plane. It is defined as one particular definite integral of the ratio between an exponential function and its argument.
Contents
Definitions
For real non zero values of x, the exponential integral Ei(x) is defined as
The Risch algorithm shows that Ei is not an elementary function. The definition above can be used for positive values of x, but the integral has to be understood in terms of the Cauchy principal value due to the singularity of the integrand at zero.
For complex values of the argument, the definition becomes ambiguous due to branch points at 0 and
(note that for positive values of x, we have
In general, a branch cut is taken on the negative real axis and E1 can be defined by analytic continuation elsewhere on the complex plane.
For positive values of the real part of
The behaviour of E1 near the branch cut can be seen by the following relation:
Properties
Several properties of the exponential integral below, in certain cases, allow one to avoid its explicit evaluation through the definition above.
Convergent series
Integrating the Taylor series for
For complex arguments off the negative real axis, this generalises to
where
This formula can be used to compute
A faster converging series was found by Ramanujan:
Asymptotic (divergent) series
Unfortunately, the convergence of the series above is slow for arguments of larger modulus. For example, for x = 10 more than 40 terms are required to get an answer correct to three significant figures. However, there is a divergent series approximation that can be obtained by integrating
which has error of order
Exponential and logarithmic behavior: bracketing
From the two series suggested in previous subsections, it follows that
The left-hand side of this inequality is shown in the graph to the left in blue; the central part
Definition by Ein
Both
(note that this is just the alternating series in the above definition of
Relation with other functions
Kummer's equation
is usually solved by the confluent hypergeometric functions
we have
for all z. A second solution is then given by E1(−z). In fact,
with the derivative evaluated at
The exponential integral is closely related to the logarithmic integral function li(x) by the formula
for non-zero real values of
The exponential integral may also be generalized to
which can be written as a special case of the incomplete gamma function:
For more information on the properties of this function, refer to the more extensive article on the incomplete gamma function.
The generalized form is sometimes called the Misra function
Including a logarithm defines the generalized integro-exponential function
The indefinite integral:
is similar in form to the ordinary generating function for
Derivatives
The derivatives of the generalised functions
Note that the function
Exponential integral of imaginary argument
If
to get a relation with the trigonometric integrals
The real and imaginary parts of
Approximations
There has been a number of approximations for the exponential integral function. These include
