 | ||
In mathematics, the logarithmic integral function or integral logarithm li(x) is a special function. It is relevant in problems of physics and has number theoretic significance, occurring in the prime number theorem as an estimate of the number of prime numbers less than a given value.
Contents
Integral representation
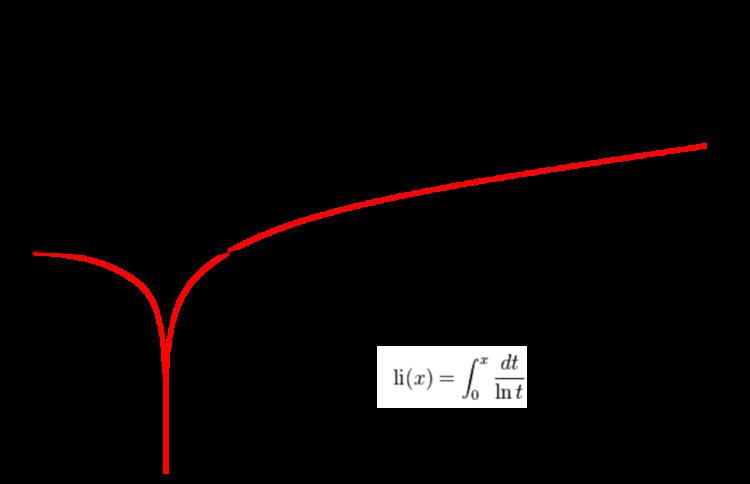
The logarithmic integral has an integral representation defined for all positive real numbers x ≠ 1 by the definite integral
Here, ln denotes the natural logarithm. The function 1/ln(t) has a singularity at t = 1, and the integral for x > 1 has to be interpreted as a Cauchy principal value,
Offset logarithmic integral
The offset logarithmic integral or Eulerian logarithmic integral is defined as
or, integrally represented
As such, the integral representation has the advantage of avoiding the singularity in the domain of integration.
This function is a very good approximation to the number of prime numbers less than x.
Special values
The function li(x) has a single positive zero; it occurs at x ≈ 1.45136 92348 ... A070769; this number is known as the Ramanujan–Soldner constant.
li(2) ≈ 1.045163 780117 492784 844588 889194 613136 522615 578151… A069284
This is
Series representation
The function li(x) is related to the exponential integral Ei(x) via the equation
which is valid for x > 0. This identity provides a series representation of li(x) as
where γ ≈ 0.57721 56649 01532 ... A001620 is the Euler–Mascheroni gamma constant. A more rapidly convergent series due to Ramanujan is
Asymptotic expansion
The asymptotic behavior for x → ∞ is
where
or
This gives the following more accurate asymptotic behaviour:
Note that, as an asymptotic expansion, this series is not convergent: it is a reasonable approximation only if the series is truncated at a finite number of terms, and only large values of x are employed. This expansion follows directly from the asymptotic expansion for the exponential integral.
Number theoretic significance
The logarithmic integral is important in number theory, appearing in estimates of the number of prime numbers less than a given value. For example, the prime number theorem states that:
where
