 | ||
In mathematics, the phrase up to appears in discussions about the elements of a set (say S), and the conditions under which subsets of those elements may be considered equivalent. The statement "elements a and b of set S are equivalent up to X" means that a and b are equivalent if criterion X (such as rotation or permutation) is ignored. That is, a and b can be transformed into one another if a transform corresponding to X (rotation, permutation etc.) is applied.
Contents
Looking at the entire set S, when X is ignored the elements can be arranged in subsets whose elements are equivalent ("equivalent up to X"). Such subsets are called "equivalence classes".
If X is some property or process, the phrase "up to X" means "disregarding a possible difference in X". For instance the statement "an integer's prime factorization is unique up to ordering", means that the prime factorization is unique if we disregard the order of the factors. We might say "the solution to an indefinite integral is f(x), up to addition by a constant", meaning that the added constant is not the focus here, the solution f(x) is, and that the addition of a constant is to be regarded as a background, of secondary focus. Further examples concerning up to isomorphism, up to permutations and up to rotations are described below.
In informal contexts, mathematicians often use the word modulo (or simply "mod") for similar purposes, as in "modulo isomorphism".
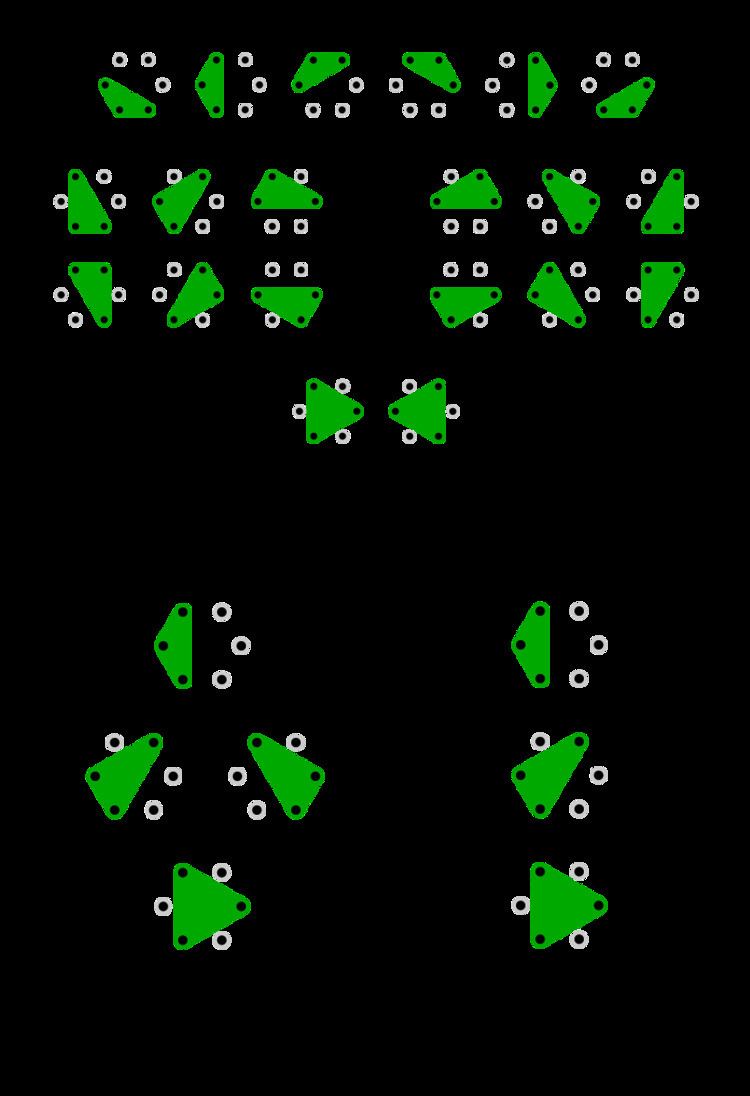
Tetris
A simple example is "there are seven reflecting tetrominos, up to rotations", which makes reference to the seven possible contiguous arrangements of tetrominoes (collections of four unit squares arranged to connect on at least one side) which are frequently thought of as the seven Tetris pieces (O, I, L, J, T, S, Z.) This could also be written "there are five tetrominos, up to reflections and rotations", which would take account of the perspective that L and J could be thought of as the same piece, reflected, as well as that S and Z could be seen as the same. The Tetris game does not allow reflections, so the former notation is likely to seem more natural.
To add in the exhaustive count, there is no formal notation. However, it is common to write "there are seven reflecting tetrominos (= 19 total) up to rotations". In this, Tetris provides an excellent example, as a reader might simply count 7 pieces × 4 rotations as 28, where some pieces (the 2×2 O being the obvious example) have fewer than four rotation states.
Eight queens
In the eight queens puzzle, if the eight queens are considered to be distinct, there are 3 709 440 distinct solutions. Normally however, the queens are considered to be identical, and one says "there are 92 (
If, in addition to treating the queens as identical, rotations and reflections of the board were allowed, we would have only 12 distinct solutions up to symmetry and the naming of the queens, signifying that two arrangements that are symmetrical to each other are considered equivalent.
Polygons
The regular n-gon, for given n, is unique up to similarity. In other words, if all similar n-gons are considered instances of the same n-gon, then there is only one regular n-gon.
Group theory
In group theory, for example, we may have a group G acting on a set X, in which case we say that two elements of X are equivalent "up to the group action" if they lie in the same orbit.
Another typical example is the statement that "there are two different groups of order 4 up to isomorphism", or "modulo isomorphism, there are two groups of order 4". This means that there are two equivalence classes of groups of order 4, assuming we consider groups to be equivalent if they are isomorphic.
Non-standard analysis
A hyperreal x and its standard part st(x) are equal up to an infinitesimal difference.
Computer science
In computer science, the term up-to techniques is a precisely defined notion that refers to certain proof techniques for (weak) bisimulation, to relate processes that only behave similarly up to unobservable steps.
