 | ||
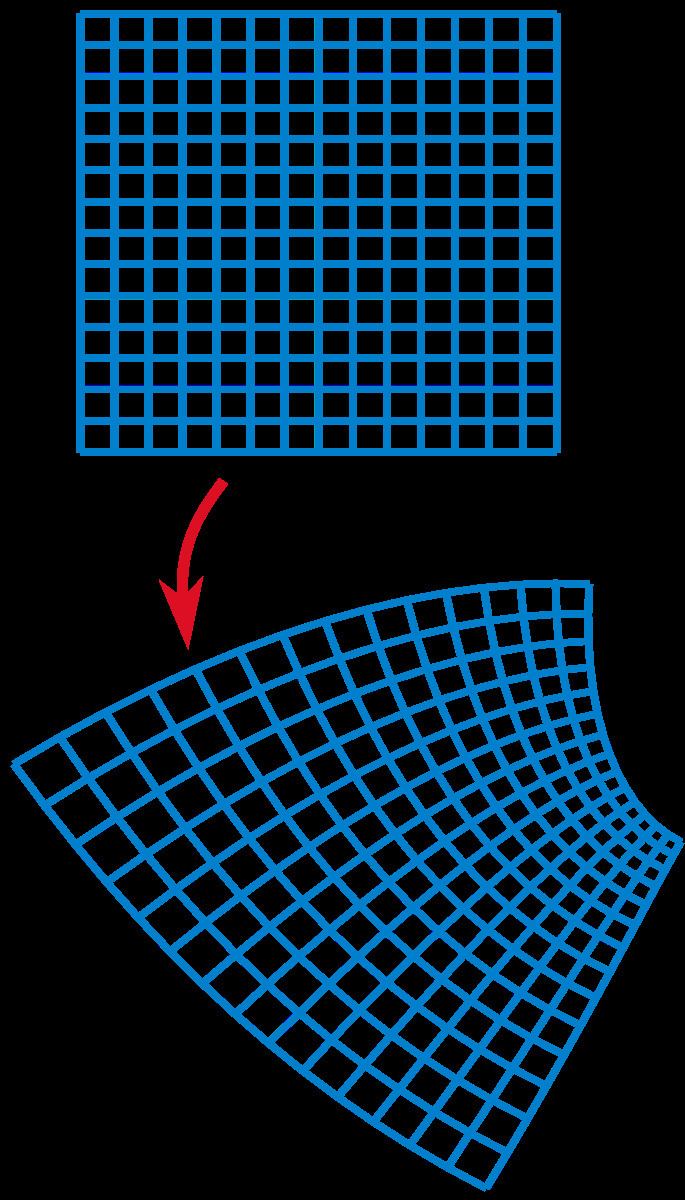
In mathematics, a conformal map is a function that preserves angles locally. In the most common case, the function has a domain and an image in the complex plane.
Contents
- Complex analysis
- Riemannian geometry
- Higher dimensional Euclidean space
- Uses
- Alternative angles
- References
More formally, let
The conformal property may be described in terms of the Jacobian derivative matrix of a coordinate transformation. If the Jacobian matrix of the transformation is everywhere a scalar times a rotation matrix, then the transformation is conformal.
Conformal maps can be defined between domains in higher-dimensional Euclidean spaces, and more generally on a Riemannian or semi-Riemannian manifold.
Complex analysis
An important family of examples of conformal maps comes from complex analysis. If
In the literature, there is another definition of conformal maps; a map
The Riemann mapping theorem, one of the profound results of complex analysis, states that any non-empty open simply connected proper subset of
A map of the extended complex plane (which is conformally equivalent to a sphere) onto itself is conformal if and only if it is a Möbius transformation. Again, for the conjugate, angles are preserved, but orientation is reversed.
An example of the latter is taking the reciprocal of the conjugate, which corresponds to circle inversion with respect to the unit circle. This can also be expressed as taking the reciprocal of the radial coordinate in circular coordinates, keeping the angle the same. See also inversive geometry.
Riemannian geometry
In Riemannian geometry, two Riemannian metrics
A diffeomorphism between two Riemannian manifolds is called a conformal map if the pulled back metric is conformally equivalent to the original one. For example, stereographic projection of a sphere onto the plane augmented with a point at infinity is a conformal map.
One can also define a conformal structure on a smooth manifold, as a class of conformally equivalent Riemannian metrics.
Higher-dimensional Euclidean space
A classical theorem of Joseph Liouville called Liouville's theorem shows the higher-dimensions have less varied conformal maps:
Any conformal map on a portion of Euclidean space of dimension greater than 2 can be composed from three types of transformation: a homothetic transformation, an isometry, and a special conformal transformation. (A special conformal transformation is the composition of a reflection and an inversion in a sphere.) Thus, the set of conformal transformations in spaces of dimension greater than 2 is much more restricted than in the planar case, where the Riemann mapping theorem provides a large set of conformal transformations.
Uses
If a function is harmonic (that is, it satisfies Laplace's equation
Conformal mappings are invaluable for solving problems in engineering and physics that can be expressed in terms of functions of a complex variable but that exhibit inconvenient geometries. By choosing an appropriate mapping, the analyst can transform the inconvenient geometry into a much more convenient one. For example, one may wish to calculate the electric field,
A large group of conformal maps for relating solutions of Maxwell’s equations was identified by Ebenezer Cunningham (1908) and Harry Bateman (1910) (see spherical wave transformation). Their training at Cambridge University had given them facility with the method of image charges and associated methods of images for spheres and inversion. As recounted by Andrew Warwick (2003) Masters of Theory:
Each four-dimensional solution could be inverted in a four-dimensional hyper-sphere of pseudo-radiusWarwick highlights (pages 404 to 424) this "new theorem of relativity" as a Cambridge response to Einstein, and as founded on exercises using the method of inversion, such as found in James Hopwood Jeans textbook Mathematical Theory of Electricity and Magnetism.
In cartography, several named map projections, including the Mercator projection and the stereographic projection are conformal. These enjoy the property that the distortion of shapes can be made as small as desired by making the diameter of the mapped region small enough. See Conformal map projection.
In general relativity, conformal maps are the simplest and thus most common type of causal transformations. Physically, these describe different universes in which all the same events and interactions are still (causally) possible, but a new additional force is necessary to effect this (that is, replication of all the same trajectories would necessitate departures from geodesic motion because the metric is different). It is often used to try to make models amenable to extension beyond curvature singularities, for example to permit description of the universe even before the big bang.
Alternative angles
A conformal map is called that because it preserves the shapes of things (at an infinitesimal scale). The term is based on the Latin prefix com- (together, with, near) and the Latin noun forma (shape, appearance). The presumption often is that the shape being preserved is measured by the standard Euclidean angle, say parameterized in degrees or radians. However, in plane mapping there are two other angles to consider: the hyperbolic angle and the slope, which is the analogue of angle for dual numbers.
Suppose
If the Jacobian
Indeed, any such
While describing analytic functions of a bireal variable, U. Bencivenga and G. Fox have written about conformal maps that preserve the hyperbolic angle. In general, a linear fractional transformation on any one of the types of complex plane listed provides a conformal map.
