Transfer matrix method (optics)

Formalism for electromagnetic waves

Below is described how the transfer matrix is applied to electromagnetic waves (for example light) of a given frequency propagating through a stack of layers at normal incidence. It can be generalized to deal with incidence at an angle, absorbing media, and media with magnetic properties. We assume that the stack layers are normal to the z axis and that the field within one layer can be represented as the superposition of a left- and right-traveling wave with wave number k ,

Because it follows from Maxwell's equation that E and F = d E / d z must be continuous across a boundary, it is convenient to represent the field as the vector ( E ( z ) , F ( z ) ) , where

Since there are two equations relating E and F to E r and E l , these two representations are equivalent. In the new representation, propagation over a distance L into the positive z direction is described by the unimodular matrix

and

Such a matrix can represent propagation through a layer if k is the wave number in the medium and L the thickness of the layer: For a system with N layers, each layer j has a transfer matrix M j , where j increases towards higher z values. The system transfer matrix is then

Typically, one would like to know the reflectance and transmittance of the layer structure. If the layer stack starts at z = 0 , then for negative z , the field is described as

where E 0 is the amplitude of the incoming wave, k L the wave number in the left medium, and r is the amplitude (not intensity!) reflectance coefficient of the layer structure. On the other side of the layer structure, the field consists of a right-propagating transmitted field

where t is the amplitude transmittance, k R is the wave number in the rightmost medium, and L ′ is the total thickness. If F L = d E L / d z and F R = d E R / d z , then we can solve

in terms of the matrix elements M m n of the system matrix M s and obtain

and

The transmittance and reflectance (i.e., the fractions of the incident intensity | E 0 | 2 transmitted and reflected by the layer) are often of more practical use and are given by T = k R k L | t | 2 and R = | r | 2 , respectively (at normal incidence).

Example

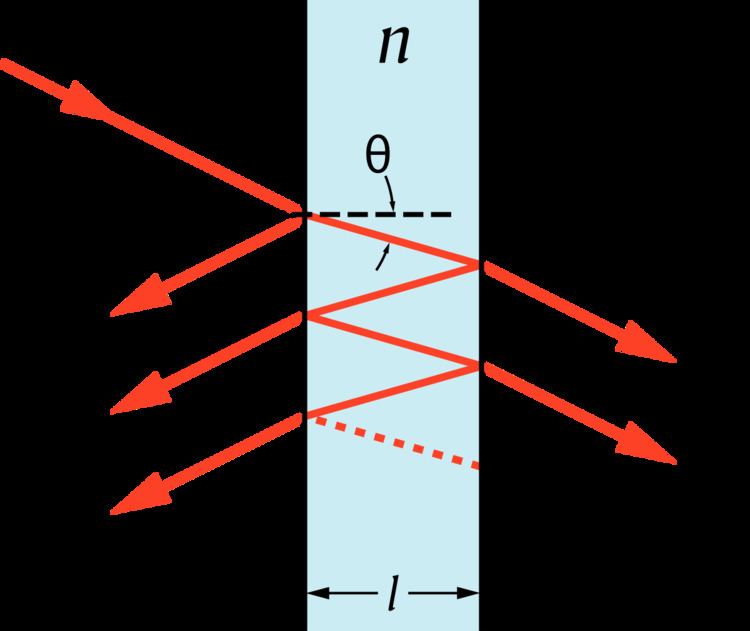
As an illustration, consider a single layer of glass with a refractive index n and thickness d suspended in air at a wave number k (in air). In glass, the wave number is k ′ = n k . The transfer matrix is

The amplitude reflection coefficient can be simplified to

This configuration effectively describes a Fabry–Pérot interferometer or etalon: for k ′ d = 0 , π , 2 π , ⋯ , the reflection vanishes.

Acoustic waves

It is possible to apply the transfer-matrix method to sound waves. Instead of the electric field E and its derivative F, the displacement u and the stress σ = C d u / d z , where C is the p-wave modulus, should be used.

Abeles matrix formalism

The Abeles matrix method is a computationally fast and easy way to calculate the specular reflectivity from a stratified interface, as a function of the perpendicular momentum transfer, Q_z:

where θ is the angle of incidence/reflection of the incident radiation and λ is the wavelength of the radiation. The measured reflectivity depends on the variation in the scattering length density (SLD) profile, ρ(z), perpendicular to the interface. Although the scattering length density profile is normally a continuously varying function, the interfacial structure can often be well approximated by a slab model in which layers of thickness (d_n), scattering length density (ρ_n) and roughness (σ_n,n+1) are sandwiched between the super- and sub-phases. One then uses a refinement procedure to minimise the differences between the theoretical and measured reflectivity curves, by changing the parameters that describe each layer.

In this description the interface is split into n layers. Since the incident neutron beam is refracted by each of the layers the wavevector, k, in layer n, is given by:

The Fresnel reflection coefficient between layer n and n+1 is then given by:

Since the interface between each layer is unlikely to be perfectly smooth the roughness/diffuseness of each interface modifies the Fresnel coefficient and is accounted for by an error function, as described by Nevot and Croce (1980).

A phase factor, β, is introduced, which accounts for the thickness of each layer.

where i 2 = − 1 . A characteristic matrix, c_n is then calculated for each layer.

The resultant matrix is defined as the product of these characteristic matrices

from which the reflectivity is calculated as: