Stochastic tunneling

Idea

Monte Carlo method-based optimization techniques sample the objective function by randomly "hopping" from the current solution vector to another with a difference in the function value of Δ E . The acceptance probability of such a trial jump is in most cases chosen to be min ( 1 ; exp ⁡ ( − β ⋅ Δ E ) ) (Metropolis criterion) with an appropriate parameter β .

The general idea of STUN is to circumvent the slow dynamics of ill-shaped energy functions that one encounters for example in spin glasses by tunneling through such barriers.

This goal is achieved by Monte Carlo sampling of a transformed function that lacks this slow dynamics. In the "standard-form" the transformation reads f S T U N := 1 − exp ⁡ ( − γ ⋅ ( E ( x ) − E o ) ) where E o is the lowest function value found so far. This transformation preserves the loci of the minima.

f S T U N is then used in place of E in the original algorithm giving a new acceptance probability of min ( 1 ; exp ⁡ ( − β ⋅ Δ f S T U N ) )

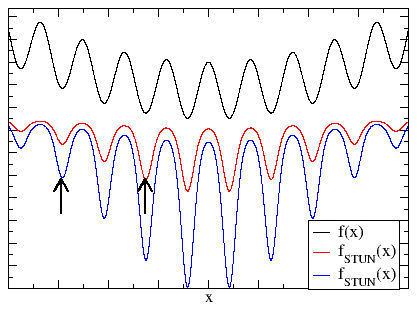
The effect of such a transformation is shown in the graph.

Dynamically Adaptive Stochastic Tunneling

A variation on always tunneling is to do so only when trapped at a local minimum. γ is then adjusted to tunnel out of the minimum and peruse a more globally optimum solution. Detrended fluctuation analysis is the recommended way of determining if trapped at a local minimum.

Other approaches