 | ||
Spin glasses and complexity
A spin glass is a disordered magnet, where the magnetic spin of the component atoms (the orientation of the north and south magnetic poles in three-dimensional space) are not aligned in a regular pattern. The term "glass" comes from an analogy between the magnetic disorder in a spin glass and the positional disorder of a conventional, chemical glass, e.g., a window glass. In window glass or any amorphous solid the atomic bond structure is highly irregular; in contrast, a crystal has a uniform pattern of atomic bonds. In ferromagnetic solid, magnetic spins all align in the same direction; this would be analogous to a crystal.
Contents
- Spin glasses and complexity
- Statistical mechanics of spin glasses and neural networks 8 3 16
- Magnetic behavior
- EdwardsAnderson model
- The model of Sherrington and Kirkpatrick
- Infinite range model
- Non ergodic behavior and applications
- History of the field
- Literature
- References
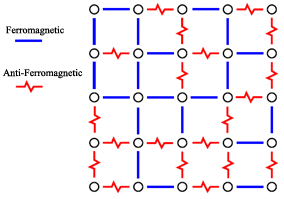
The individual atomic bonds in a spin glass are a mixture of roughly equal numbers of ferromagnetic bonds (where neighbors have the same orientation) and antiferromagnetic bonds (where neighbors have exactly the opposite orientation: north and south poles are flipped 180 degrees). These patterns of aligned and misaligned atomic magnets create what are known as frustrated interactions - distortions in the geometry of atomic bonds compared to what would be seen in a regular, fully aligned solid. They may also create situations where more than one geometric arrangement of atoms is stable.
Spin glasses and the complex internal structures that arise within them are termed "metastable" because they are "stuck" in stable configurations other than the lowest-energy configuration (which would be aligned and ferromagnetic). The mathematical complexity of these structures are difficult but fruitful to study experimentally or in simulations, with applications to artificial neural networks in computer science in addition to physics, chemistry, and materials science.
Statistical mechanics of spin glasses and neural networks 8 3 16
Magnetic behavior
It is the time dependence which distinguishes spin glasses from other magnetic systems.
Above the spin glass transition temperature, Tc, the spin glass exhibits typical magnetic behaviour (such as paramagnetism).
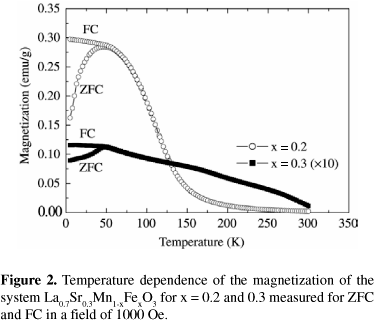
If a magnetic field is applied as the sample is cooled to the transition temperature, magnetization of the sample increases as described by the Curie law. Upon reaching Tc, the sample becomes a spin glass and further cooling results in little change in magnetization. This is referred to as the field-cooled magnetization.
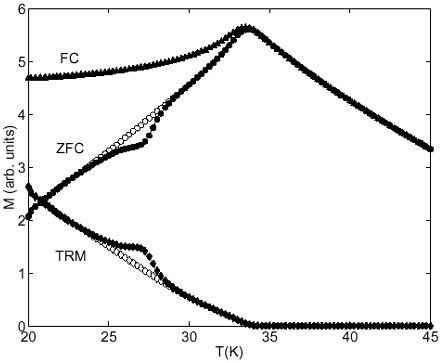
When the external magnetic field is removed, the magnetization of the spin glass falls rapidly to a lower value known as the remanent magnetization.
Magnetization then decays slowly as it approaches zero (or some small fraction of the original value—this remains unknown). This decay is non-exponential and no simple function can fit the curve of magnetization versus time adequately. This slow decay is particular to spin glasses. Experimental measurements on the order of days have shown continual changes above the noise level of instrumentation.
Spin glasses differ from ferromagnetic materials by the fact that after the external magnetic field is removed from a ferromagnetic substance, the magnetization remains indefinitely at the remanent value. Paramagnetic materials differ from spin glasses by the fact that, after the external magnetic field is removed, the magnetization rapidly falls to zero, with no remanent magnetization. In each case the decay is rapid and exponential.
If the sample is cooled below Tc in the absence of an external magnetic field and a magnetic field is applied after the transition to the spin glass phase, there is a rapid initial increase to a value called the zero-field-cooled magnetization. A slow upward drift then occurs toward the field-cooled magnetization.
Surprisingly, the sum of the two complicated functions of time (the zero-field-cooled and remanent magnetizations) is a constant, namely the field-cooled value, and thus both share identical functional forms with time, at least in the limit of very small external fields.
Edwards–Anderson model
In this model, we have spins arranged on a
where
Solving for the free energy using the replica method, below a certain temperature, a new magnetic phase called the spin glass phase (or glassy phase) of the system is found to exist which is characterized by a vanishing magnetization
The model of Sherrington and Kirkpatrick
In addition to unusual experimental properties, spin glasses are the subject of extensive theoretical and computational investigations. A substantial part of early theoretical work on spin glasses dealt with a form of mean field theory based on a set of replicas of the partition function of the system.
An important, exactly solvable model of a spin glass was introduced by D. Sherrington and S. Kirkpatrick in 1975. It is an Ising model with long range frustrated ferro- as well as antiferromagnetic couplings. It corresponds to a mean field approximation of spin glasses describing the slow dynamics of the magnetization and the complex non-ergodic equilibrium state.
Unlike the Edwards–Anderson (EA) model, in the system though only two spins interactions are considered, the range of each interaction can be potentially infinite (of the order of the size of the lattice). Therefore, we see that any two spins can be lined with a ferromagnetic or an antiferromagnetic bond and the distribution of these is given exactly as in the case of Edwards–Anderson model. The Hamiltonian for SK model is very similar to the EA model:
where
The formalism of replica mean field theory has also been applied in the study of neural networks, where it has enabled calculations of properties such as the storage capacity of simple neural network architectures without requiring a training algorithm (such as backpropagation) to be designed or implemented.
More realistic spin glass models with short range frustrated interactions and disorder, like the Gaussian model where the couplings between neighboring spins follow a Gaussian distribution, have been studied extensively as well, especially using Monte Carlo simulations. These models display spin glass phases bordered by sharp phase transitions.
Besides its relevance in condensed matter physics, spin glass theory has acquired a strongly interdisciplinary character, with applications to neural network theory, computer science, theoretical biology, econophysics etc.
Infinite-range model
The infinite-range model is a generalization of the Sherrington–Kirkpatrick model where we not only consider two spin interactions but
where
The order parameters for this system are given by the magnetization
Non-ergodic behavior and applications
A so-called non-ergodic behavior happens in spin glasses below the freezing temperature
History of the field
A detailed account of the history of spin glasses from the early 1960s to the late 1980s can be found in a series of popular articles by Philip W. Anderson in Physics Today.
