Smoluchowski coagulation equation - Alchetron, the free social encyclopedia

In statistical physics, the Smoluchowski coagulation equation is a population balance equation introduced by Marian Smoluchowski in a seminal 1916 publication, describing the time evolution of the number density of particles as they coagulate (in this context "clumping together") to size x at time t.

Equation

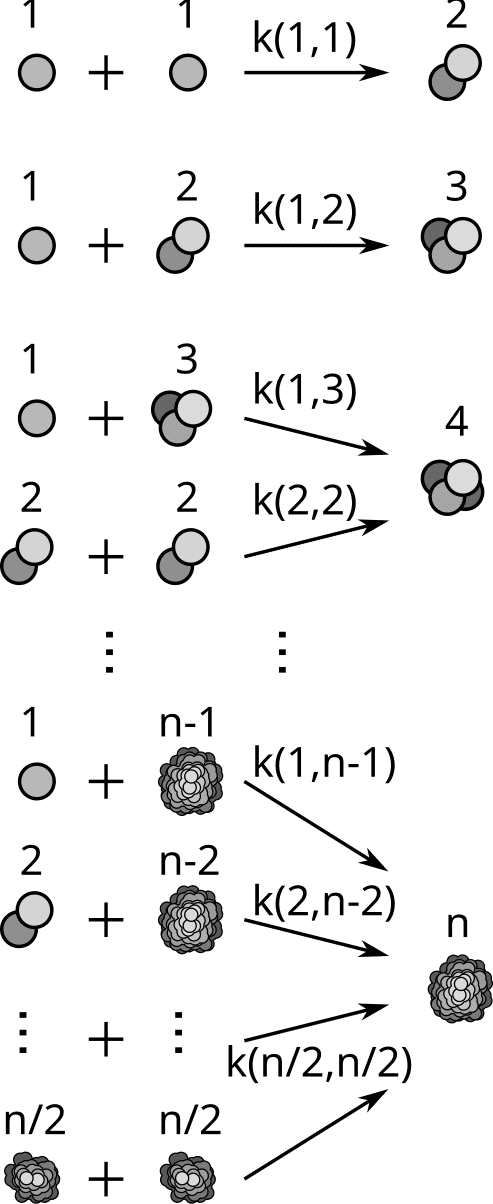
The distribution of particle size change in time according to the interrelation of all particles of the system. Therefore, the Smoluchowski coagulation equation is an integrodifferential equation of the particle-size distribution. In the case when the sizes of the coagulated particles are continuous variables, the equation involves an integral:

∂ n ( x , t ) ∂ t = 1 2 ∫ 0 x K ( x − y , y ) n ( x − y , t ) n ( y , t ) d y − ∫ 0 ∞ K ( x , y ) n ( x , t ) n ( y , t ) d y .

If dy is interpreted as a discrete measure, i.e. when particles join in discrete sizes, then the discrete form of the equation is a summation:

∂ n ( x i , t ) ∂ t = 1 2 ∑ j = 1 i − 1 K ( x i − x j , x j ) n ( x i − x j , t ) n ( x j , t ) − ∑ j = 1 ∞ K ( x i , x j ) n ( x i , t ) n ( x j , t ) .

There exist a unique solution for a chosen kernel function.

Coagulation kernel

The operator, K, is known as the coagulation kernel and describes the rate at which particles of size x 1 coagulate with particles of size x 2 . Analytic solutions to the equation exist when the kernel takes one of three simple forms:

K = 1 , K = x 1 + x 2 , K = x 1 x 2 ,

known as the constant, additive, and multiplicative kernels respectively.

However, in most practical applications the kernel takes on a significantly more complex form. For example, the free-molecular kernel which describes collisions in a dilute gas-phase system,

K = π k B T 2 ( 1 m ( x 1 ) + 1 m ( x 2 ) ) 1 / 2 ( d ( x 1 ) + d ( x 2 ) ) 2 .

Some coagulation kernels account for a specific fractal dimension of the clusters, as in the diffusion-limited aggregation:

K = 2 3 k B T η ( x 1 1 / y 1 + x 2 1 / y 2 ) ( x 1 − 1 / y 1 + x 2 − 1 / y 2 ) ,

or Reaction-limited aggregation:

K = 2 3 k B T η ( x 1 x 2 ) γ W ( x 1 1 / y 1 + x 2 1 / y 2 ) ( x 1 − 1 / y 1 + x 2 − 1 / y 2 ) ,

where y 1 , y 2 are fractal dimensions of the clusters, k B is the Boltzmann constant, T is the temperature, W is the Fuchs stability ratio, η is the continuous phase viscosity, and γ is the exponent of the product kernel, usually considered a fitting parameter.

Generally the coagulation equations that result from such physically realistic kernels are not solvable, and as such, it is necessary to appeal to numerical methods. Most of deterministic methods can be used when there is only one particle property (x) of interest, the two principal ones being the method of moments and sectional methods. In the multi-variate case, however, when two or more properties (such as size, shape, composition, etc.) are introduced, one has to seek special approximation methods that suffer less from curse of dimensionality. Approximation based on Gaussian radial basis functions has been successfully applied to the coagulation equation in more than one dimension.

When the accuracy of the solution is not of primary importance, stochastic particle (Monte Carlo) methods are an attractive alternative.

Condensation-driven aggregation

In addition to aggregation, particles may also grow in size by condensation, deposition or by accretion. Hassan and Hassan recently proposed a condensation-driven aggregation (CDA) model in which aggregating particles keep growing continuously between merging upon collision. The CDA model can be understood by the following reaction scheme

A x ( t ) + A y ( t ) ⟶ v ( x , t ) A ( α + 1 ) ( x + y ) ( t + τ ) ,

where A x ( t ) denotes the aggregate of size x at time t and τ is the elapsed time. This reaction scheme can be described by the following generalized Smoluchowski equation

[ ∂ ∂ t + ∂ ∂ x v ( x , t ) ] n ( x , t ) = − n ( x , t ) ∫ 0 ∞ K ( x , y ) n ( y , t ) d y + 1 2 ∫ 0 x d y K ( y , x − y ) n ( y , t ) n ( x − y , t ) .

Considering that a particle of size x grows due to condensation between collision time τ ( x ) equal to inverse of ∫ 0 ∞ K ( x , y ) n ( y , t ) d y by an amount α x i.e.

v ( x , t ) = α x τ ( x ) = α x ∫ 0 ∞ d y K ( x , y ) n ( y , t ) .

One can solve the generalized Smoluchowski equation for constant kernel to give

n ( x , t ) ∼ t − ( 2 + 2 α ) e − x t 1 + 2 α ,

which exhibits dynamic scaling. A simple fractal analysis reveals that the condensation-driven aggregation can be best described fractal of dimension

d f = 1 1 + 2 α .

Interestingly, the d f th moment of n ( x , t ) is always a conserved quantity which is responsible for fixing all the exponents of the dynamic scaling. Such conservation law has also been found in Cantor set too.

References

Smoluchowski coagulation equation Wikipedia

(Text) CC BY-SA

Contents

Equation

Coagulation kernel

Condensation-driven aggregation

References