Cantor set

Construction and formula of the ternary set

The Cantor ternary set C is created by iteratively deleting the open middle third from a set of line segments. One starts by deleting the open middle third (1/3, 2/3) from the interval [0, 1], leaving two line segments: [0, 1/3] ∪ [2/3, 1]. Next, the open middle third of each of these remaining segments is deleted, leaving four line segments: [0, 1/9] ∪ [2/9, 1/3] ∪ [2/3, 7/9] ∪ [8/9, 1]. This process is continued ad infinitum, where the nth set is

The Cantor ternary set contains all points in the interval [0, 1] that are not deleted at any step in this infinite process:

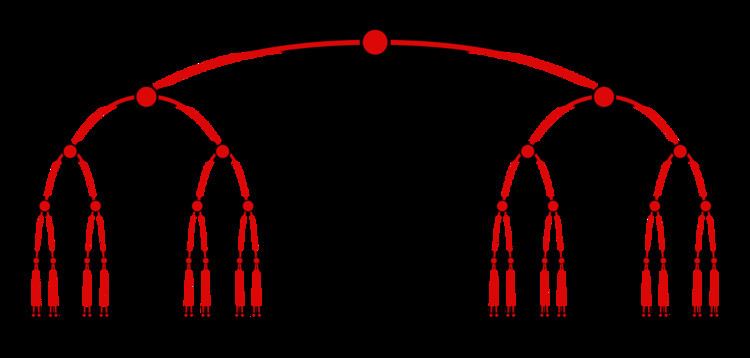
The first six steps of this process are illustrated below.

Using the idea of self-similar transformations, T L ( x ) = x / 3 , T R ( x ) = ( 2 + x ) / 3 and C n = T L ( C n − 1 ) ∪ T R ( C n − 1 ) , the explicit closed formulas for the Cantor set are,:

or

This process of removing middle thirds is a simple example of a finite subdivision rule.

It is perhaps most intuitive to think about the Cantor set as the set of real numbers between zero and one whose ternary expansion in base three doesn't contain the digit 1. As the above diagram shows, the Cantor ternary set is in bijection with the set of paths in a full binary tree on countably many nodes. Such a path is completely determined by an infinite series of instructions determining at each node whether we go left or right as we traverse the diagram. This in turn describes the ternary expansion of the number. For example, such a path might begin (left, right, right, left, left...) which describes the ternary number 0.02200.... In particular, the Cantor set is canonically in bijection with the set of binary sequences.

Composition

Since the Cantor set is defined as the set of points not excluded, the proportion (i.e., measure) of the unit interval remaining can be found by total length removed. This total is the geometric progression

So that the proportion left is 1 – 1 = 0.

This calculation shows that the Cantor set cannot contain any interval of non-zero length. In fact, it may seem surprising that there should be anything left — after all, the sum of the lengths of the removed intervals is equal to the length of the original interval. However, a closer look at the process reveals that there must be something left, since removing the "middle third" of each interval involved removing open sets (sets that do not include their endpoints). So removing the line segment (¹/₃, ²/₃) from the original interval [0, 1] leaves behind the points ¹/₃ and ²/₃. Subsequent steps do not remove these (or other) endpoints, since the intervals removed are always internal to the intervals remaining. So the Cantor set is not empty, and in fact contains an uncountably infinite number of points (as follows from the above description in terms of paths in an infinite binary tree).

It may appear that only the endpoints are left, but that is not the case either. To find it we can take the k th moment M k of the remaining intervals at the n th step of the construction process. The moment M k is

where it is assumed that x i s are the size of the remaining intervals. In fact, all the 2 n intervals are of the same size i.e. x 1 = x 2 = . . . . = x 2 n = 3 − n . Thus

and we find

regardless of the value of n . This very k = log ⁡ 2 log ⁡ 3 is actually the fractal dimension of the Cantor set. We can thus conclude that the set is not empty which is one more surprising feature of the Cantor set. This is true even for random and stochastic Cantor set. Indeed, the number 1/4, for example, is in the bottom third, so it is not removed at the first step, and is in the top third of the bottom third, and is in the bottom third of that, and in the top third of that, and so on ad infinitum—alternating between top and bottom thirds. Since it is never in one of the middle thirds, it is never removed, and yet it is also not one of the endpoints of any middle third. The number 3/10 is also in the Cantor set and is not an endpoint.

In the sense of cardinality, most members of the Cantor set are not endpoints of deleted intervals. Since each step removes a finite number of intervals and the number of steps is countable, the set of endpoints is countable while the whole Cantor set is uncountable.

Cardinality

It can be shown that there are as many points left behind in this process as there were to begin with, and that therefore, the Cantor set is uncountable. To see this, we show that there is a function f from the Cantor set C to the closed interval [0,1] that is surjective (i.e. f maps from C onto [0,1]) so that the cardinality of C is no less than that of [0,1]. Since C is a subset of [0,1], its cardinality is also no greater, so the two cardinalities must in fact be equal, by the Cantor–Bernstein–Schroeder theorem.

To construct this function, consider the points in the [0, 1] interval in terms of base 3 (or ternary) notation. Recall that some points admit more than one representation in this notation, as for example ¹/₃, that can be written as 0.1₃ but also as 0.022222...₃, and ²/₃, that can be written as 0.2₃ but also as 0.12222...₃. (This alternative recurring representation of a number with a terminating numeral occurs in any positional system.) When we remove the middle third, this contains the numbers with ternary numerals of the form 0.1xxxxx...₃ where xxxxx...₃ is strictly between 00000...₃ and 22222...₃. So the numbers remaining after the first step consist of

This can be summarized by saying that those numbers that admit a ternary representation such that the first digit after the decimal point is not 1 are the ones remaining after the first step.

The second step removes numbers of the form 0.01xxxx...₃ and 0.21xxxx...₃, and (with appropriate care for the endpoints) it can be concluded that the remaining numbers are those with a ternary numeral where neither of the first two digits is 1. Continuing in this way, for a number not to be excluded at step n, it must have a ternary representation whose nth digit is not 1. For a number to be in the Cantor set, it must not be excluded at any step, it must admit a numeral representation consisting entirely of 0s and 2s. It is worth emphasising that numbers like 1, ¹/₃ = 0.1₃ and ⁷/₉ = 0.21₃ are in the Cantor set, as they have ternary numerals consisting entirely of 0s and 2s: 1 = 0.2222...₃, ¹/₃ = 0.022222...₃ and ⁷/₉ = 0.2022222...₃. So while a number in C may have either a terminating or a recurring ternary numeral, one of its representations will consist entirely of 0s and 2s.

The function from C to [0,1] is defined by taking the numeral that does consist entirely of 0s and 2s, replacing all the 2s by 1s, and interpreting the sequence as a binary representation of a real number. In a formula,

For any number y in [0,1], its binary representation can be translated into a ternary representation of a number x in C by replacing all the 1s by 2s. With this, f(x) = y so that y is in the range of f. For instance if y = ³/₅ = 0.100110011001...₂, we write x = 0.200220022002...₃ = ⁷/₁₀. Consequently, f is surjective; however, f is not injective — interestingly enough, the values for which f(x) coincides are those at opposing ends of one of the middle thirds removed. For instance, ⁷/₉ = 0.2022222...₃ and ⁸/₉ = 0.2200000...₃ so f(⁷/₉) = 0.101111...₂ = 0.11₂ = f(⁸/₉).

So there are as many points in the Cantor set as there are in [0, 1], and the Cantor set is uncountable (see Cantor's diagonal argument). However, the set of endpoints of the removed intervals is countable, so there must be uncountably many numbers in the Cantor set which are not interval endpoints. As noted above, one example of such a number is ¼, which can be written as 0.02020202020...₃ in ternary notation. In fact, given any x ∈ [ − 1 , 1 ] , there exist a , b ∈ C such that x = a − b . This was first demonstrated by Steinhaus in 1917, who proved, via a geometric argument, the equivalent assertion that { ( x , y ) ∈ R 2 : y = x + c } ∩ ( C × C ) ≠ ∅ for every c ∈ [ − 1 , 1 ] . Since this construction provides an injection from [ − 1 , 1 ] to C × C , we have | C × C | ≥ | [ − 1 , 1 ] | = c as an immediate corollary. Assuming that | A × A | = | A | for any infinite set A (a statement shown to be equivalent to the axiom of choice by Tarski), this provides another demonstration that | C | = c .

The Cantor set contains as many points as the interval from which it is taken, yet itself contains no interval of nonzero length. The irrational numbers have the same property, but the Cantor set has the additional property of being closed, so it is not even dense in any interval, unlike the irrational numbers which are dense in every interval.

It has been conjectured that all algebraic irrational numbers are normal. Since members of the Cantor set are not normal, this would imply that all members of the Cantor set are either rational or transcendental.

Self-similarity

The Cantor set is the prototype of a fractal. It is self-similar, because it is equal to two copies of itself, if each copy is shrunk by a factor of 3 and translated. More precisely, there are two functions, the left and right self-similarity transformations, T L ( x ) = x / 3 and T R ( x ) = ( 2 + x ) / 3 , which leave the Cantor set invariant up to homeomorphism: T L ( C ) ≅ T R ( C ) ≅ C .

Repeated iteration of T L and T R can be visualized as an infinite binary tree. That is, at each node of the tree, one may consider the subtree to the left or to the right. Taking the set { T L , T R } together with function composition forms a monoid, the dyadic monoid.

The automorphisms of the binary tree are its hyperbolic rotations, and are given by the modular group. Thus, the Cantor set is a homogeneous space in the sense that for any two points x and y in the Cantor set C , there exists a homeomorphism h : C → C with h ( x ) = y . These homeomorphisms can be expressed explicitly, as Möbius transformations.

The Hausdorff dimension of the Cantor set is equal to ln(2)/ln(3) ≈ 0.631.

The Hausdorff Dimension Theorem

An essential property of Cantor sets is giving sufficiency of fractals for any given Hausdorff dimension r :

Theorem. For any given r > 0 , there are uncountable fractals with Hausdorff dimension r in n-dimensional Euclidean space R n , ( n ≥ − [ − r ] ) .

Topological and analytical properties

Although "the" Cantor set typically refers to the original, middle-thirds Cantor described above, topologists often talk about "a" Cantor set, which means any topological space that is homeomorphic (topologically equivalent) to it.

As the above summation argument shows, the Cantor set is uncountable but has Lebesgue measure 0. Since the Cantor set is the complement of a union of open sets, it itself is a closed subset of the reals, and therefore a complete metric space. Since it is also totally bounded, the Heine–Borel theorem says that it must be compact.

For any point in the Cantor set and any arbitrarily small neighborhood of the point, there is some other number with a ternary numeral of only 0s and 2s, as well as numbers whose ternary numerals contain 1s. Hence, every point in the Cantor set is an accumulation point (also called a cluster point or limit point) of the Cantor set, but none is an interior point. A closed set in which every point is an accumulation point is also called a perfect set in topology, while a closed subset of the interval with no interior points is nowhere dense in the interval.

Every point of the Cantor set is also an accumulation point of the complement of the Cantor set.

For any two points in the Cantor set, there will be some ternary digit where they differ — one will have 0 and the other 2. By splitting the Cantor set into "halves" depending on the value of this digit, one obtains a partition of the Cantor set into two closed sets that separate the original two points. In the relative topology on the Cantor set, the points have been separated by a clopen set. Consequently, the Cantor set is totally disconnected. As a compact totally disconnected Hausdorff space, the Cantor set is an example of a Stone space.

As a topological space, the Cantor set is naturally homeomorphic to the product of countably many copies of the space { 0 , 1 } , where each copy carries the discrete topology. This is the space of all sequences in two digits

which can also be identified with the set of 2-adic integers. The basis for the open sets of the product topology are cylinder sets; the homeomorphism maps these to the subspace topology that the Cantor set inherits from the natural topology on the real number line. This characterization of the Cantor space as a product of compact spaces gives a second proof that Cantor space is compact, via Tychonoff's theorem.

From the above characterization, the Cantor set is homeomorphic to the p-adic integers, and, if one point is removed from it, to the p-adic numbers.

The Cantor set is a subset of the reals, which are a metric space with respect to the ordinary distance metric; therefore the Cantor set itself is a metric space, by using that same metric. Alternatively, one can use the p-adic metric on 2 N : given two sequences ( x n ) , ( y n ) ∈ 2 N , the distance between them is d ( ( x n ) , ( y n ) ) = 1 / k , where k is the smallest index such that x k ≠ y k ; if there is no such index, then the two sequences are the same, and one defines the distance to be zero. These two metrics generate the same topology on the Cantor set.

We have seen above that the Cantor set is a totally disconnected perfect compact metric space. Indeed, in a sense it is the only one: every nonempty totally disconnected perfect compact metric space is homeomorphic to the Cantor set. See Cantor space for more on spaces homeomorphic to the Cantor set.

The Cantor set is sometimes regarded as "universal" in the category of compact metric spaces, since any compact metric space is a continuous image of the Cantor set; however this construction is not unique and so the Cantor set is not universal in the precise categorical sense. The "universal" property has important applications in functional analysis, where it is sometimes known as the representation theorem for compact metric spaces.

For any integer q ≥ 2, the topology on the group G=Z_q^ω (the countable direct sum) is discrete. Although the Pontrjagin dual Γ is also Z_q^ω, the topology of Γ is compact. One can see that Γ is totally disconnected and perfect - thus it is homeomorphic to the Cantor set. It is easiest to write out the homeomorphism explicitly in the case q=2. (See Rudin 1962 p 40.)

Measure and probability

The Cantor set can be seen as the compact group of binary sequences, and as such, it is endowed with a natural Haar measure. When normalized so that the measure of the set is 1, it is a model of an infinite sequence of coin tosses. Furthermore, one can show that the usual Lebesgue measure on the interval is an image of the Haar measure on the Cantor set, while the natural injection into the ternary set is a canonical example of a singular measure. It can also be shown that the Haar measure is an image of any probability, making the Cantor set a universal probability space in some ways.

In Lebesgue measure theory, the Cantor set is an example of a set which is uncountable and has zero measure.

Cantor numbers

If we define a Cantor number as a member of the Cantor set, then

Smith–Volterra–Cantor set

Instead of repeatedly removing the middle third of every piece as in the Cantor set, we could also keep removing any other fixed percentage (other than 0% and 100%) from the middle. In the case where the middle ⁸/₁₀ of the interval is removed, we get a remarkably accessible case — the set consists of all numbers in [0,1] that can be written as a decimal consisting entirely of 0s and 9s.

By removing progressively smaller percentages of the remaining pieces in every step, one can also construct sets homeomorphic to the Cantor set that have positive Lebesgue measure, while still being nowhere dense. See Smith–Volterra–Cantor set for an example.

Stochastic Cantor set

Natural fractals do not appear in a blink of an eye rather through evolution in time accompanied by some randomness since nature likes to enjoy freedom of choice. One can modify the construction of the Cantor set by dividing randomly instead of equally. Besides, to incorporate time we can divide only one of the available intervals at each step instead of dividing all the available intervals. In the case of stochastic triadic Cantor set the resulting process can be described by the following rate equation

and for the stochastic dyadic Cantor set

where c ( x , t ) d x is the number of intervals of size between x and x + d x . In the case of triadic Cantor set the fractal dimension is 0.5616 which is less than its deterministic counterpart 0.6309 . In the case of stochastic dyadic Cantor set the fractal dimension is p which is again less than that of its deterministic counterpart ln ⁡ ( 1 + p ) / ln ⁡ 2 . In the case of stochastic dyadic Cantor set the solution for c ( x , t ) exhibits dynamic scaling as its solution in the long-time limit is t − ( 1 + d f ) e − x t where the fractal dimension of the stochastic dyadic Cantor set d f = p .

Cantor dust

Cantor dust is a multi-dimensional version of the Cantor set. It can be formed by taking a finite Cartesian product of the Cantor set with itself, making it a Cantor space. Like the Cantor set, Cantor dust has zero measure.

A different 2D analogue of the Cantor set is the Sierpinski carpet, where a square is divided up into nine smaller squares, and the middle one removed. The remaining squares are then further divided into nine each and the middle removed, and so on ad infinitum. The 3D analogue of this is the Menger sponge.

Historical remarks

Cantor himself defined the set in a general, abstract way, and mentioned the ternary construction only in passing, as an example of a more general idea, that of a perfect set that is nowhere dense. The original paper provides several different constructions of the abstract concept.

This set would have been considered abstract at the time when Cantor devised it. Cantor himself was led to it by practical concerns about the set of points where a trigonometric series might fail to converge. The discovery did much to set him on the course for developing an abstract, general theory of infinite sets.

A column capital from the Ancient Egyptian site of the island of Philae carries a pattern which resembles the Cantor set. Cantor may have seen the image, as his cousin was an Egyptologist.