Vertices 60 Automorphisms 120 | Edges 120 | |
 | ||
Properties Quartic graph, Hamiltonian, regular | ||
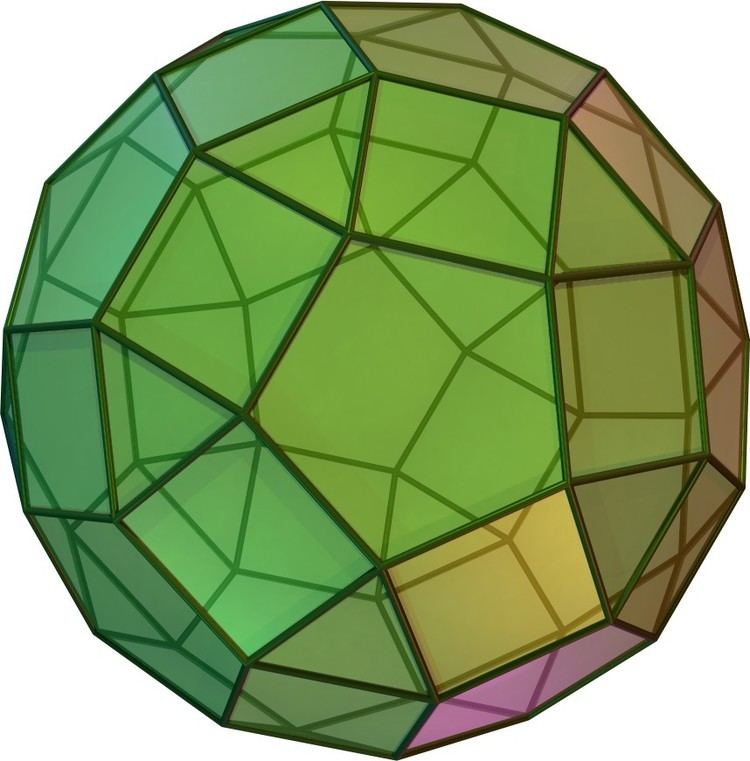
In geometry, the rhombicosidodecahedron, or small rhombicosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed of two or more types of regular polygon faces.
Contents
- Geometric relations
- Cartesian coordinates
- Orthogonal projections
- Spherical tiling
- Symmetry mutations
- Johnson solids
- Vertex arrangement
- Rhombicosidodecahedral graph
- References
It has 20 regular triangular faces, 30 square faces, 12 regular pentagonal faces, 60 vertices and 120 edges.
The name rhombicosidodecahedron refers to the fact that the 30 square faces lie in the same planes as the 30 faces of the rhombic triacontahedron which is dual to the icosidodecahedron.
It can also be called an expanded or cantellated dodecahedron or icosahedron, from truncation operations on either uniform polyhedron.
Geometric relations
If you expand an icosahedron by moving the faces away from the origin the right amount, without changing the orientation or size of the faces, and do the same to its dual dodecahedron, and patch the square holes in the result, you get a rhombicosidodecahedron. Therefore, it has the same number of triangles as an icosahedron and the same number of pentagons as a dodecahedron, with a square for each edge of either.
The rhombicosidodecahedron shares the vertex arrangement with the small stellated truncated dodecahedron, and with the uniform compounds of six or twelve pentagrammic prisms.
The Zometool kits for making geodesic domes and other polyhedra use slotted balls as connectors. The balls are "expanded" rhombicosidodecahedra, with the squares replaced by rectangles. The expansion is chosen so that the resulting rectangles are golden rectangles.
Twelve of the 92 Johnson solids are derived from the rhombicosidodecahedron, four of them by rotation of one or more pentagonal cupolae: the gyrate, parabigyrate, metabigyrate and trigyrate rhombicosidodecahedron. Eight more can be constructed by removing up to three cupolae, sometimes also rotating one or more of the other cupolae.
Cartesian coordinates
Cartesian coordinates for the vertices of a rhombicosidodecahedron with edge length 2 centered at the origin are all even permutations of:
(±1, ±1, ±φ3),(±φ2, ±φ, ±2φ),(±(2+φ), 0, ±φ2),where φ = 1 + √5/2 is the golden ratio.
Orthogonal projections
The rhombicosidodecahedron has five special orthogonal projections, centered, on a vertex, on two types of edges, and three types of faces: triangles, squares, and pentagons. The last two correspond to the A2 and H2 Coxeter planes.
Spherical tiling
The rhombicosidodecahedron can also be represented as a spherical tiling, and projected onto the plane via a stereographic projection. This projection is conformal, preserving angles but not areas or lengths. Straight lines on the sphere are projected as circular arcs on the plane.
Symmetry mutations
This polyhedron is topologically related as a part of a sequence of cantellated polyhedra with vertex figure (3.4.n.4), which continues as tilings of the hyperbolic plane. These vertex-transitive figures have (*n32) reflectional symmetry.
Johnson solids
There are 13 related Johnson solids, 5 by diminishment, and 8 including gyrations:
Vertex arrangement
The rhombicosidodecahedron shares its vertex arrangement with three nonconvex uniform polyhedra: the small stellated truncated dodecahedron, the small dodecicosidodecahedron (having the triangular and pentagonal faces in common), and the small rhombidodecahedron (having the square faces in common).
It also shares its vertex arrangement with the uniform compounds of six or twelve pentagrammic prisms.
Rhombicosidodecahedral graph
In the mathematical field of graph theory, a rhombicosidodecahedral graph is the graph of vertices and edges of the rhombicosidodecahedron, one of the Archimedean solids. It has 60 vertices and 120 edges, and is a quartic graph Archimedean graph.
