← {\displaystyle {\boldsymbol {\leftarrow }}} t-transitive, t ≥ 2 → {\displaystyle {\boldsymbol {\rightarrow }}} regular | ← {\displaystyle {\boldsymbol {\leftarrow }}} strongly regular | |
 | ||
→ {\displaystyle {\boldsymbol {\rightarrow }}} edge-transitive and regular | ||
In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other. A regular graph with vertices of degree k is called a k‑regular graph or regular graph of degree k. Also, from the Handshaking lemma, a regular graph of odd degree will contain even number of vertices.
Contents
Regular graphs of degree at most 2 are easy to classify: A 0-regular graph consists of disconnected vertices, a 1-regular graph consists of disconnected edges, and a 2-regular graph consists of disconnected cycles and infinite chains.
A 3-regular graph is known as a cubic graph.
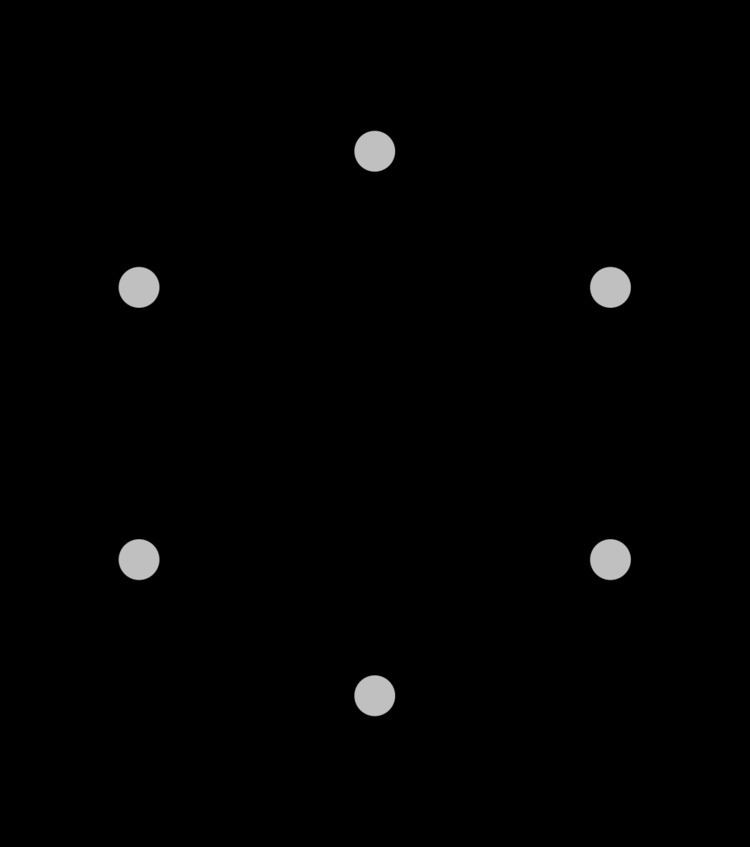
A strongly regular graph is a regular graph where every adjacent pair of vertices has the same number l of neighbors in common, and every non-adjacent pair of vertices has the same number n of neighbors in common. The smallest graphs that are regular but not strongly regular are the cycle graph and the circulant graph on 6 vertices.
The complete graph
A theorem by Nash-Williams says that every k‑regular graph on 2k + 1 vertices has a Hamiltonian cycle.
Existence
It is well known that the necessary and sufficient conditions for a
Algebraic properties
Let A be the adjacency matrix of a graph. Then the graph is regular if and only if
A regular graph of degree k is connected if and only if the eigenvalue k has multiplicity one. The "only if" direction is a consequence of the Perron–Frobenius theorem.
There is also a criterion for regular and connected graphs : a graph is connected and regular if and only if the matrix of ones J, with
Let G be a k-regular graph with diameter D and eigenvalues of adjacency matrix
Generation
Regular graphs may be generated by the GenReg program.
