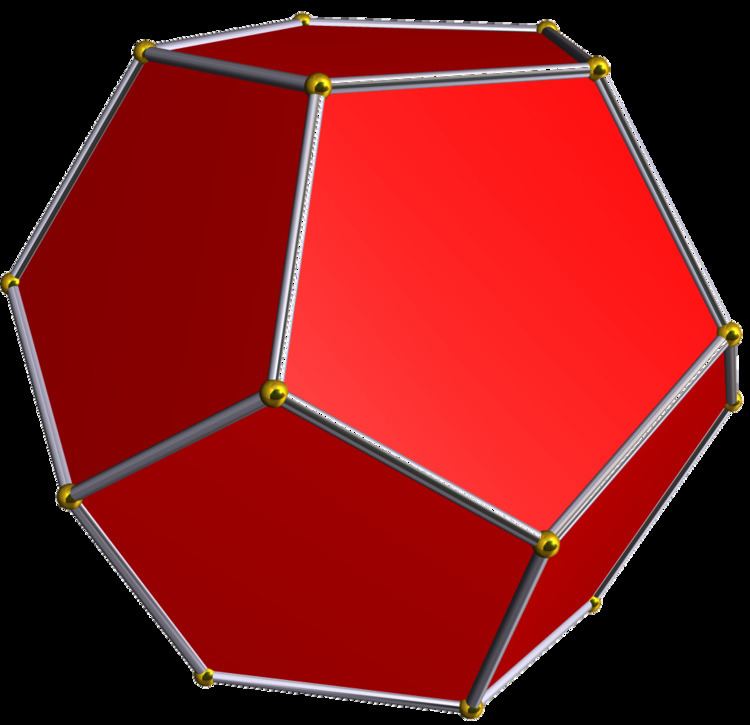
Number of faces 12 Number of vertices 20 Number of edges 30 | Volume (15+7×√5)/4 × a³ Surface area 3×√(25+10×√5) × a² Base shape Pentagon | |
 | ||
Shapes with similar faces | ||
Make 3d solid shapes dodecahedron
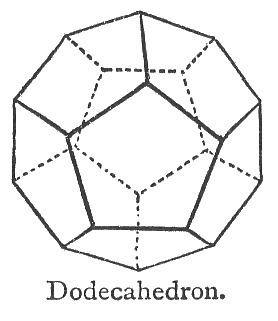
In geometry, a dodecahedron (Greek δωδεκάεδρον, from δώδεκα dōdeka "twelve" + ἕδρα hédra "base", "seat" or "face") is any polyhedron with twelve flat Faces. The most familiar dodecahedron is the regular dodecahedron, which is a Platonic solid. There are also three regular star dodecahedra, which are constructed as stellations of the convex form. All of these have icosahedral symmetry, order 120.
Contents
- Make 3d solid shapes dodecahedron
- How to draw dodecahedron the 5 platonic solids
- Pentagonal dodecahedron
- Pyritohedron
- Crystal pyrite
- Cartesian coordinates
- Geometric freedom
- Tetartoid
- Variations
- Rhombic dodecahedron
- Other dodecahedra
- References
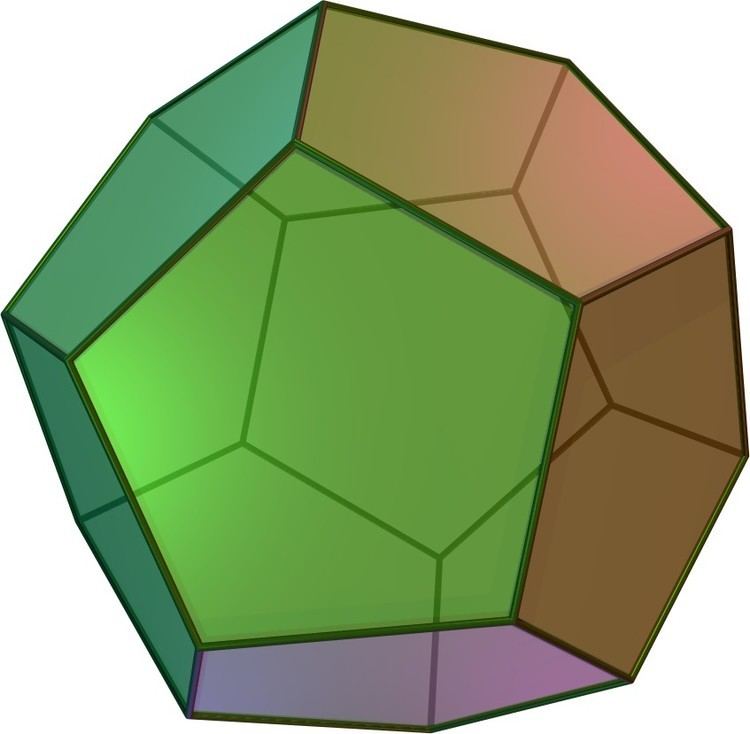
The pyritohedron is an irregular pentagonal dodecahedron, having the same topology as the regular one but pyritohedral symmetry while the tetartoid has tetrahedral symmetry. The rhombic dodecahedron, seen as a limiting case of the pyritohedron has octahedral symmetry. The elongated dodecahedron and trapezo-rhombic dodecahedron variations, along with the rhombic dodecahedra are space-filling. There are a large number of other dodecahedra.
How to draw dodecahedron the 5 platonic solids
Pentagonal dodecahedron
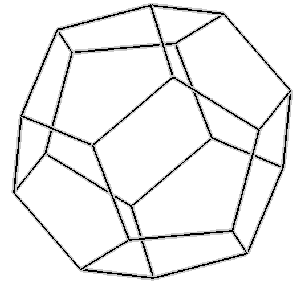
The convex regular dodecahedron is one of the five regular Platonic solids and can be represented by its Schläfli symbol {5, 3}.
The dual polyhedron is the regular icosahedron {3, 5}, having five equilateral triangles around each vertex.
In crystallography, two important dodecahedra can occur as crystal forms in some symmetry classes of the cubic crystal system that are topologically equivalent to the regular dodecahedron but less symmetrical: the pyritohedron with pyritohedral symmetry, and the tetartoid with tetrahedral symmetry:
Pyritohedron
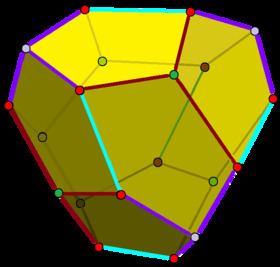
A pyritohedron is a dodecahedron with pyritohedral (Th) symmetry. Like the regular dodecahedron, it has twelve identical pentagonal Faces, with three meeting in each of the 20 Vertices. However, the pentagons are not constrained to be regular, and the underlying atomic arrangement has no true fivefold symmetry axes. Its 30 Edges are divided into two sets – containing 24 and 6 Edges of the same length. The only axes of rotational symmetry are three mutually perpendicular twofold axes and four threefold axes.
Although regular dodecahedra do not exist in crystals, the pyritohedron form occurs in the crystals of the mineral pyrite, and it may be an inspiration for the discovery of the regular Platonic solid form. Note that the true regular dodecahedron can occur as a shape for quasicrystals with icosahedral symmetry, which includes true fivefold rotation axes.
Crystal pyrite
Its name comes from one of the two common crystal habits shown by pyrite, the other one being the cube.
Cartesian coordinates
The coordinates of the eight Vertices of the original cube are:
(±1, ±1, ±1)The coordinates of the 12 vertices of the cross-edges are:
(0, ±(1 + h), ±(1 − h2))(±(1 + h), ±(1 − h2), 0)(±(1 − h2), 0, ±(1 + h))where h is the height of the wedge-shaped "roof" above the faces of the cube. When h = 1, the six cross-edges degenerate to points and a rhombic dodecahedron is formed. When h = 0, the cross-edges are absorbed in the facets of the cube, and the pyritohedron reduces to a cube. When h = √5 − 1/2, the inverse of the golden ratio, the result is a regular dodecahedron.
A reflected pyritohedron is made by swapping the nonzero coordinates above. The two pyritohedra can be superimposed to give the compound of two dodecahedra as seen in the image here.
Geometric freedom
The pyritohedron has a geometric degree of freedom with limiting cases of a cubic convex hull at one limit of colinear edges, and a rhombic dodecahedron as the other limit as 6 edges are degenerated to length zero. The regular dodecahedron represents a special intermediate case where all edges and angles are equal.
Tetartoid
A tetartoid (also tetragonal pentagonal dodecahedron, pentagon-tritetrahedron, and tetrahedric pentagon dodecahedron) is a dodecahedron with Chiral tetrahedral symmetry (T). Like the regular dodecahedron, it has twelve identical pentagonal faces, with three meeting in each of the 20 vertices. However, the pentagons are not regular and the figure has no fivefold symmetry axes.
Although regular dodecahedra do not exist in crystals, the tetartoid form does. The name tetartoid comes from the Greek root for one-fourth because it has one fourth of full octahedral symmetry, and half of pyritohedral symmetry. The mineral cobaltite can have this symmetry form.
Its topology can be as a cube with square faces bisected into 2 rectangles like the pyritohedron, and then the bisection lines are slanted retaining 3-fold rotation at the 8 corners.
Cartesian coordinates
The following points are vertices of a tetartoid pentagon under tetrahedral symmetry:
(a, b, c); (−a, −b, c); (−n/d1, −n/d1, n/d1); (−c, −a, b); (−n/d2, n/d2, n/d2),under the following conditions:
0 ≤ a ≤ b ≤ c,n = a2c − bc2,d1 = a2 − ab + b2 + ac − 2bc,d2 = a2 + ab + b2 − ac − 2bc,nd1d2 ≠ 0.Variations
It can be seen as a tetrahedron, with edges divided into 3 segments, along with a center point of each triangular face. In Conway polyhedron notation it can be seen as gT, a gyro tetrahedron.
Rhombic dodecahedron
The rhombic dodecahedron is a zonohedron with twelve rhombic faces and octahedral symmetry. It is dual to the quasiregular cuboctahedron (an Archimedean solid) and occurs in nature as a crystal form. The rhombic dodecahedron packs together to fill space.
The rhombic dodecahedron can be seen as a degenerate pyritohedron where the 6 special edges have been reduced to zero length, reducing the pentagons into rhombic faces.
The rhombic dodecahedron has several stellations, the first of which is also a parallelohedral spacefiller.
Another important rhombic dodecahedron, the Bilinski dodecahedron, has twelve faces congruent to those of the rhombic triacontahedron, i.e. the diagonals are in the ratio of the golden ratio. It is also a zonohedron and was described by Bilinski in 1960. This figure is another spacefiller, and can also occur in non-periodic spacefillings along with the rhombic triacontahedron, the rhombic icosahedron and rhombic hexahedra.
Other dodecahedra
There are 6,384,634 topologically distinct convex dodecahedra, excluding mirror images, having at least 8 vertices. (Two polyhedra are "topologically distinct" if they have intrinsically different arrangements of faces and vertices, such that it is impossible to distort one into the other simply by changing the lengths of edges or the angles between edges or faces.)
Topologically distinct dodecahedra (excluding pentagonal and rhombic forms)
