 | ||
In mathematics, the restriction of a function f is a new function f|A obtained by choosing a smaller domain A for the original function f. The notation
Contents
Formal definition
Let f : E → F be a function from a set E to a set F, so that the domain of f is in E (
Informally, the restriction of f to A is the same function as f, but is only defined on
If the function f is thought of as a relation
Examples
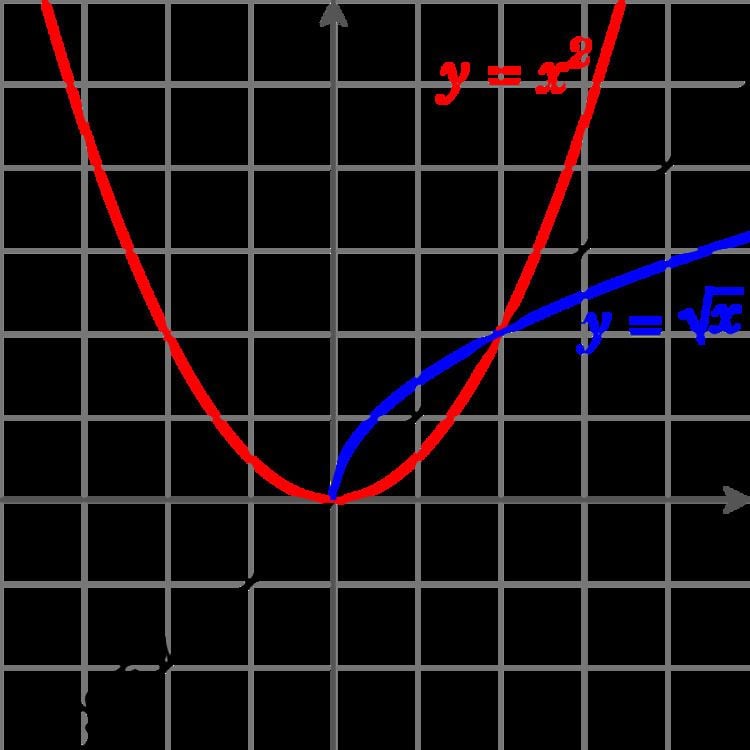
- The restriction of the non-injective function
f : R → R ; x ↦ x 2 R + = [ 0 , ∞ ) is the injectionf : R + → R ; x ↦ x 2 - The factorial function is the restriction of the gamma function to the integers.
Properties of restrictions
Inverse functions
For a function to have an inverse, it must be one-to-one. If a function f is not one-to-one, it may be possible to define a partial inverse of f by restricting the domain. For example, the function
is not one-to-one, since x2 = (−x)2. However, the function becomes one-to-one if we restrict to the domain x ≥ 0, in which case
(If we instead restrict to the domain x ≤ 0, then the inverse is the negative of the square root of y.) Alternatively, there is no need to restrict the domain if we are content with the inverse being a multivalued function:
Selection operators
In relational algebra, a selection (sometimes called a restriction to avoid confusion with SQL's use of SELECT) is a unary operation written as
The selection
The selection
Thus, the selection operator restricts to a subset of the entire database.
The Pasting Lemma
The pasting lemma is a result in topology that relates the continuity of a function with the continuity of its restrictions to subsets.
Let
This result allows one to take two continuous functions defined on closed (or open) subsets of a topological space and create a new one.
Sheaves
Sheaves provide a way of generalizing restrictions to objects besides functions.
In sheaf theory, one assigns an object
The collection of all such objects is called a sheaf. If only the first two properties are satisfied, it is a pre-sheaf.
Left- and right-restriction
More generally, the restriction (or domain restriction or left-restriction) A ◁ R of a binary relation R between E and F may be defined as a relation having domain A, codomain F and graph G(A ◁ R) = {(x, y) ∈ G(R) | x ∈ A} . Similarly, one can define a right-restriction or range restriction R ▷ B. Indeed, one could define a restriction to n-ary relations, as well as to subsets understood as relations, such as ones of E × F for binary relations. These cases do not fit into the scheme of sheaves.
Anti-restriction
The domain anti-restriction (or domain subtraction) of a function or binary relation R (with domain E and codomain F) by a set A may be defined as (E A) ◁ R; it removes all elements of A from the domain E. It is sometimes denoted A ⩤ R. Similarly, the range anti-restriction (or range subtraction) of a function or binary relation R by a set B is defined as R ▷ (F B); it removes all elements of B from the codomain F. It is sometimes denoted R ⩥ B.
