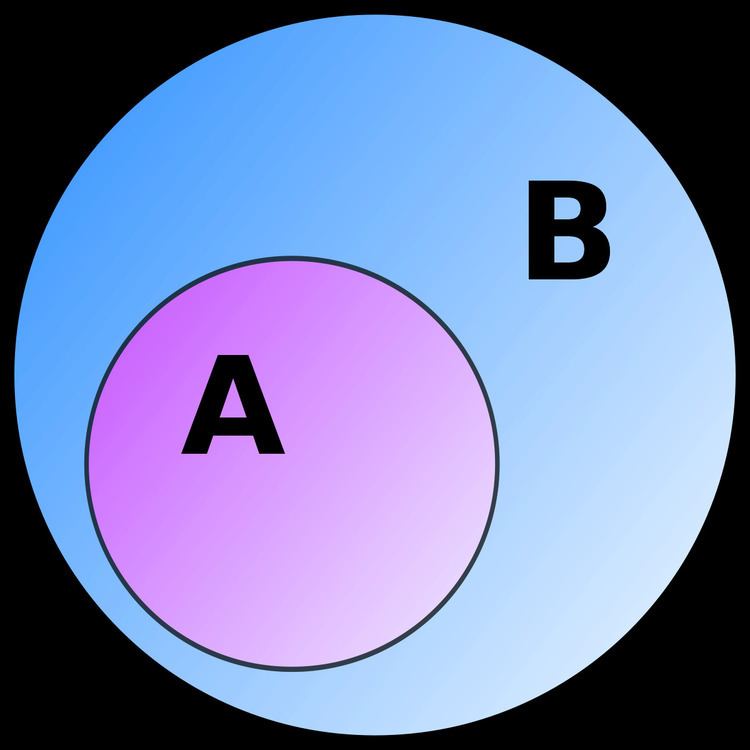
Inclusion map - Alchetron, The Free Social Encyclopedia

In mathematics, if A is a subset of B , then the inclusion map (also inclusion function, insertion, or canonical injection) is the function ι that sends each element, x , of A to x , treated as an element of B :

ι : A → B , ι ( x ) = x .

A "hooked arrow" ↪ is sometimes used in place of the function arrow above to denote an inclusion map.

This and other analogous injective functions from substructures are sometimes called natural injections.

Given any morphism f between objects X and Y, if there is an inclusion map into the domain ι : A → X , then one can form the restriction fi of f. In many instances, one can also construct a canonical inclusion into the codomain R→Y known as the range of f.

Applications of inclusion maps

Inclusion maps tend to be homomorphisms of algebraic structures; thus, such inclusion maps are embeddings. More precisely, given a sub-structure closed under some operations, the inclusion map will be an embedding for tautological reasons. For example, for a binary operation ⋆ , to require that

ι ( x ⋆ y ) = ι ( x ) ⋆ ι ( y )

is simply to say that ⋆ is consistently computed in the sub-structure and the large structure. The case of a unary operation is similar; but one should also look at nullary operations, which pick out a constant element. Here the point is that closure means such constants must already be given in the substructure.

Inclusion maps are seen in algebraic topology where if A is a strong deformation retract of X, the inclusion map yields an isomorphism between all homotopy groups (i.e. is a homotopy equivalence).

Inclusion maps in geometry come in different kinds: for example embeddings of submanifolds. Contravariant objects such as differential forms restrict to submanifolds, giving a mapping in the other direction. Another example, more sophisticated, is that of affine schemes, for which the inclusions

Spec ⁡ ( R / I ) → Spec ⁡ ( R )

and

Spec ⁡ ( R / I 2 ) → Spec ⁡ ( R )

may be different morphisms, where R is a commutative ring and I an ideal.

References

Inclusion map Wikipedia

(Text) CC BY-SA