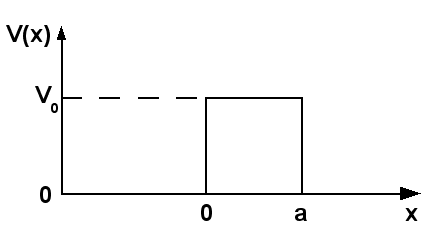
Rectangular potential barrier - Alchetron, the free social encyclopedia

In quantum mechanics, the rectangular (or, at times, square) potential barrier is a standard one-dimensional problem that demonstrates the phenomena of wave-mechanical tunneling (also called "quantum tunneling") and wave-mechanical reflection. The problem consists of solving the one-dimensional time-independent Schrödinger equation for a particle encountering a rectangular potential energy barrier. It is usually assumed, as here, that a free particle impinges on the barrier from the left.

Although a particle hypothetically behaving as a point mass would be reflected, a particle actually behaving as a matter wave has a finite probability that it will penetrate the barrier and continue its travel as a wave on the other side. In classical wave-physics, this effect is known as evanescent wave coupling. The likelihood that the particle will pass through the barrier is given by the transmission coefficient, whereas the likelihood that it is reflected is given by the reflection coefficient. Schrödinger's wave-equation allows these coefficients to be calculated.

Calculation

The time-independent Schrödinger equation for the wave function ψ ( x ) reads

H ψ ( x ) = [ − ℏ 2 2 m d 2 d x 2 + V ( x ) ] ψ ( x ) = E ψ ( x )

where H is the Hamiltonian, ℏ is the (reduced) Planck constant, m is the mass, E the energy of the particle and

V ( x ) = V 0 [ Θ ( x ) − Θ ( x − a ) ]

is the barrier potential with height V 0 > 0 and width a . Θ ( x ) = 0 , x < 0 ; Θ ( x ) = 1 , x > 0

is the Heaviside step function.

The barrier is positioned between x = 0 and x = a . The barrier can be shifted to any x position without changing the results. The first term in the Hamiltonian, − ℏ 2 2 m d 2 d x 2 ψ is the kinetic energy.

The barrier divides the space in three parts ( x < 0 , 0 < x < a , x > a ). In any of these parts, the potential is constant, meaning that the particle is quasi-free, and the solution of the Schrödinger equation can be written as a superposition of left and right moving waves (see free particle). If E > V 0

ψ L ( x ) = A r e i k 0 x + A l e − i k 0 x x < 0 ψ C ( x ) = B r e i k 1 x + B l e − i k 1 x 0 < x < a ψ R ( x ) = C r e i k 0 x + C l e − i k 0 x x > a

where the wave numbers are related to the energy via

k 0 = 2 m E / ℏ 2 x < 0 o r x > a k 1 = 2 m ( E − V 0 ) / ℏ 2 0 < x < a .

The index r/l on the coefficients A and B denotes the direction of the velocity vector. Note that, if the energy of the particle is below the barrier height, k 1 becomes imaginary and the wave function is exponentially decaying within the barrier. Nevertheless, we keep the notation r/l even though the waves are not propagating anymore in this case. Here we assumed E ≠ V 0 . The case E = V 0 is treated below.

The coefficients A , B , C have to be found from the boundary conditions of the wave function at x = 0 and x = a . The wave function and its derivative have to be continuous everywhere, so.

ψ L ( 0 ) = ψ C ( 0 ) d d x ψ L ( 0 ) = d d x ψ C ( 0 ) ψ C ( a ) = ψ R ( a ) d d x ψ C ( a ) = d d x ψ R ( a ) .

Inserting the wave functions, the boundary conditions give the following restrictions on the coefficients

A r + A l = B r + B l i k 0 ( A r − A l ) = i k 1 ( B r − B l ) B r e i a k 1 + B l e − i a k 1 = C r e i a k 0 + C l e − i a k 0 i k 1 ( B r e i a k 1 − B l e − i a k 1 ) = i k 0 ( C r e i a k 0 − C l e − i a k 0 ) .

E = V0

If the energy equals the barrier height, the solutions of the Schrödinger equation in the barrier region are not exponentials anymore but linear functions of the space coordinate

ψ C ( x ) = B 1 + B 2 x 0 < x < a .

The complete solution of the Schrödinger equation is found in the same way as above by matching wave functions and their derivatives at x = 0 and x = a . That results in the following restrictions on the coefficients:

A r + A l = B 1 i k 0 ( A r − A l ) = B 2 B 1 + B 2 a = C r e i a k 0 + C l e − i a k 0 B 2 = i k 0 ( C r e i a k 0 − C l e − i a k 0 ) .

Transmission and reflection

At this point, it is instructive to compare the situation to the classical case. In both cases, the particle behaves as a free particle outside of the barrier region. A classical particle with energy E larger than the barrier height V 0 would always pass the barrier, and a classical particle with E < V 0 incident on the barrier would always get reflected.

To study the quantum case, consider the following situation: a particle incident on the barrier from the left side ( A r ). It may be reflected ( A l ) or transmitted ( C r ).

To find the amplitudes for reflection and transmission for incidence from the left, we put in the above equations A r = 1 (incoming particle), A l = r (reflection), C l =0 (no incoming particle from the right), and C r = t (transmission). We then eliminate the coefficients B l , B r from the equation and solve for r and t .

The result is:

t = 4 k 0 k 1 e − i a ( k 0 − k 1 ) ( k 0 + k 1 ) 2 − e 2 i a k 1 ( k 0 − k 1 ) 2 r = ( k 0 2 − k 1 2 ) sin ⁡ ( a k 1 ) 2 i k 0 k 1 cos ⁡ ( a k 1 ) + ( k 0 2 + k 1 2 ) sin ⁡ ( a k 1 ) .

Due to the mirror symmetry of the model, the amplitudes for incidence from the right are the same as those from the left. Note that these expressions hold for any energy E > 0 .

E < V0

The surprising result is that for energies less than the barrier height, E < V 0 there is a non-zero probability

T = | t | 2 = 1 1 + V 0 2 sinh 2 ⁡ ( k 1 a ) 4 E ( V 0 − E )

for the particle to be transmitted through the barrier, with k 1 = 2 m ( V 0 − E ) / ℏ 2 . This effect, which differs from the classical case, is called quantum tunneling. The transmission is exponentially suppressed with the barrier width, which can be understood from the functional form of the wave function: Outside of the barrier it oscillates with wave vector k 0 , whereas within the barrier it is exponentially damped over a distance 1 / k 1 . If the barrier is much larger than this decay length, the left and right part are virtually independent and tunneling as a consequence is suppressed.

E > V0

In this case

T = | t | 2 = 1 1 + V 0 2 sin 2 ⁡ ( k 1 a ) 4 E ( E − V 0 ) ,

where k 1 = 2 m ( E − V 0 ) / ℏ 2 .

Equally surprising is that for energies larger than the barrier height, E > V 0 , the particle may be reflected from the barrier with a non-zero probability

R = | r | 2 = 1 − T .

This reflection probability is in fact oscillating with k 1 a and only in the limit E ≫ V 0 approaches the classical result r = 0 , no reflection. Note that the probabilities and amplitudes as written are for any energy (above/below) the barrier height.

E = V0

The transmission probability at E = V 0 evaluates to

T = 1 1 + m a 2 V 0 / 2 ℏ 2 .

Remarks and applications

The calculation presented above may at first seem unrealistic and hardly useful. However it has proved to be a suitable model for a variety of real-life systems. One such example are interfaces between two conducting materials. In the bulk of the materials, the motion of the electrons is quasi-free and can be described by the kinetic term in the above Hamiltonian with an effective mass m . Often the surfaces of such materials are covered with oxide layers or are not ideal for other reasons. This thin, non-conducting layer may then be modeled by a barrier potential as above. Electrons may then tunnel from one material to the other giving rise to a current.

The operation of a scanning tunneling microscope (STM) relies on this tunneling effect. In that case, the barrier is due to the gap between the tip of the STM and the underlying object. Since the tunnel current depends exponentially on the barrier width, this device is extremely sensitive to height variations on the examined sample.

The above model is one-dimensional, while space is three-dimensional. One should solve the Schrödinger equation in three dimensions. On the other hand, many systems only change along one coordinate direction and are translationally invariant along the others; they are separable. The Schrödinger equation may then be reduced to the case considered here by an ansatz for the wave function of the type: Ψ ( x , y , z ) = ψ ( x ) ϕ ( y , z ) .

For another, related model of a barrier, see Delta potential barrier (QM), which can be regarded as a special case of the finite potential barrier. All results from this article immediately apply to the delta potential barrier's taking the limits V 0 → ∞ , a → 0 while keeping V 0 a = λ 2 m 2 constant.

References

Rectangular potential barrier Wikipedia

(Text) CC BY-SA

Contents

Calculation

E = V0

Transmission and reflection

E < V0

E > V0

E = V0

Remarks and applications

References