 | ||
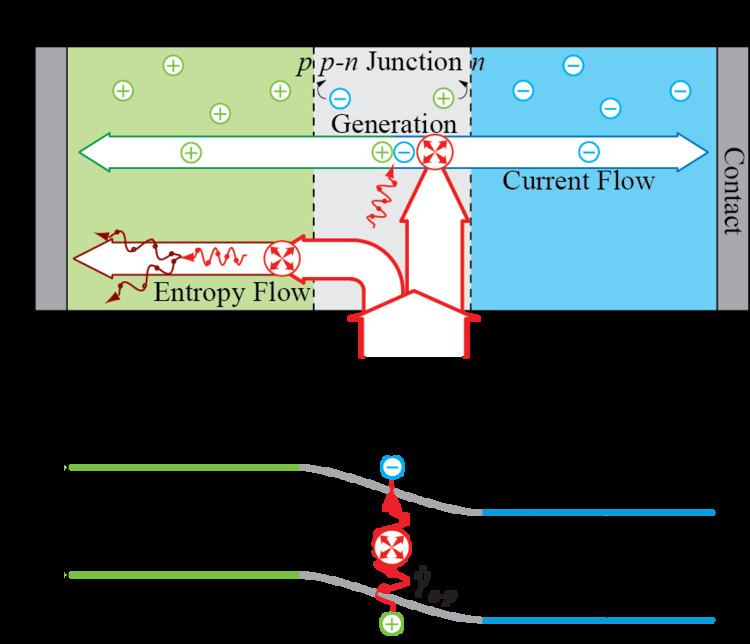
A phonovoltaic (pV) cell converts vibrational (phonons) energy into a direct current much like the photovoltaic effect in a photovoltaic (PV) cell converts light (photon) into power. That is, it uses a p-n junction to separate the electrons and holes generated as valence electrons absorb optical phonons more energetic than the band gap, and then collects them in the metallic contacts for use in a circuit. The pV cell is an application of heat transfer physics and competes with other thermal energy harvesting devices like the thermoelectric generator.
Contents
- Satisfying the laws of thermodynamics
- Non equilibrium optical phonon population and the nanoscale requirement
- Entropy generation and efficiency
- The electron phonon coupling
- The phonon phonon coupling
- The suitability of graphene as a phonovoltaic material
- References
While the thermoelectric generator converts heat, a broad spectrum of phonon and electron energy, to electricity, the pV cell converts only a narrow band of phonon energy, i.e., only the most energetic optical phonon modes. A narrow band of excited optical phonons has much less entropy than heat. Thus, the pV cell can exceed the thermoelectric efficiency. However, exciting and harvesting the optical phonon poses a challenge.
Satisfying the laws of thermodynamics
By the first law of thermodynamics, the excitation driving electron generation in both photo- and phonovoltaic cells, i.e., the photon or phonon, must have more energy than the semiconductor band gap. For a PV cell, many materials are available with a band gap (
By the second law of thermodynamics, the excitation must be "hotter" than the cell for power generation to occur. In a PV, the light comes from an outside source, for example, the sun, which is nearly 6000 Kelvin, whereas the PV is around 300 Kelvin. Thus, the second law is satisfied and energy conversion is possible. However, the crystal vibrations driving power generation in a pV are intrinsic to the material itself. As such, they can not be imported from an outside source like the sun, but must instead be excited by some other process until they are hotter than the cell. The temperature of the optical phonon population is calculated by comparing the number of optical phonon to the number expected at a given temperature, which comes from the Bose-Einstein statistics.
Non-equilibrium optical phonon population and the nanoscale requirement
There are a number of ways to excite a population of vibrations, i.e., create a hot optical phonon population. For example, if the electron population is excited, using a laser or electric field, they will typically relax by emitting optical phonons. Additionally, a hot molecular gas can impart its vibrations to a crystal when chemisorbed. Regardless of method, the conversion efficiency is limited by the optical phonon temperature achieved as compared to the electron temperature within the device due to Carnot's theorem.
In a nanoscale device, this temperature is approximately equal to the temperature of the device itself. However, in a macroscale device the generated electrons accumulate faster than they are collected. Thus, the electron population is heated up to the optical phonon temperature and further generation is inhibited. The down-conversion is simultaneously inhibited as the acoustic phonon population is heated to the optical phonon temperature. Thus, the large pV cell develops a near-equilibrium state where it is heated. At best, it will act like a thermoelectric generator and exhibit thermoelectric effects. Such a device is called a thermovoltaic, rather than a phonovoltaic.
Entropy generation and efficiency
Entropy generation and inefficiency in a PV cell is the result of photons more energetic than the band gap producing electrons with kinetic energy in addition to the potential energy provided by the band gap. Similarly, optical phonon energy in excess of the band gap generates an entropy flow in the pV cell, rather than electric power. The energy efficiency (
In addition this typical inefficiency, hot optical phonon populations tend to downconvert into multiple low-energy, acoustic phonon modes (whereas photons typically do not downconvert into low energy infrared waves). This efficiency (
where
Finally, entropy is generated in both pV and PV cells due to the inefficient separation of the generated electrons and holes. This efficiency (
where
Thus, the overall efficiency (
where the temperature independent terms become the material figure of merit (
If the band gap and optical phonon mode are resonant, and the optical phonon tends to generate electrons, the phonovoltaic cell can approach the Carnot limit as
The electron-phonon coupling
The electron-phonon coupling is responsible for electron generation in the pV cell. In this phenomenon, the phonon leads to ion motion which perturbs the highest occupied valence state (HOS). This state begins to overlap with the lowest unoccupied conduction state (LUS), and the electron can switch states if energy and momentum are conserved. If it does, an electron-hole pair is generated.
Using a taylor expansion of the change in electron potential,
where
where
The phonon-phonon coupling
Competing with the generation of electrons is the downconversion of optical phonons into multiple acoustic phonons. The coupling arises from the crystal Hamiltonian (H) expanded in terms of the ionic displacement (
where
Typically, up- and down-conversion is dominated by the third-order interaction. Thus, the perturbation Hamiltonian used in Fermi's golden rule for phonon up- and downconversion is
where
where two phonons are produced with polarization
The suitability of graphene as a phonovoltaic material
As outlined above, an efficient pV cell requires a material with an optical phonon mode more energetic than the bandgap, which in turn is much more energetic than the thermal energy at the intended operating temperature
Very few materials offer this combination of properties. Indeed, the vast majority of crystals are have optical phonon energies limited to below 50 meV, and those with more energetic optical phonons tend to have much more energetic band gaps. In general, a material with a first-row element (periodic table) is required to have a highly energetic optical phonon. However, the high electronegativity of a first-row elements tends to create a very large band gap, as in diamond and the boron nitride allotropes. Graphene is one of the few materials which diverges from this trend, with no bandgap and an exceptionally energetic optical phonon mode near 200 meV. . Thus, graphene has been the initial target for development of a phonovoltaic material through the opening and tuning of its bandgap .
Opening and tuning the bandgap of graphene has received substantial attention, and numerous strategies have been suggested and investigated. These include the use of uniaxial strain, electric fields, and chemical doping and functionalization. In general, these mechanisms work by either changing the symmetry of graphene (both Carbon atoms in the unit cell are identical) or hybridization (
In the first phonovoltaic material investigations, it has been suggested that the latter technique destroys the electron-phonon coupling while the former preserves it. In particular, these investigations predict that hydrogenating graphene, to produce graphane, reduces the electron-phonon coupling so substantially that the material figure of merit vanishes; and that doping graphene with boron nitride maintains the strong electron-phonon coupling in graphene, such that its figure of merit is predicted to reach 0.65 and enable heat harvesting with twice the efficiency of a typical thermoelectric generator.
