Optic equation

Solution

All solutions in integers a, b, c are given in terms of positive integer parameters m, n, k by

where m and n are coprime.

Appearances in geometry

The optic equation, permitting but not requiring integer solutions, appears in several contexts in geometry.

In a bicentric quadrilateral, the inradius r, the circumradius R, and the distance x between the incenter and the circumcenter are related by Fuss' theorem according to

and the distances of the incenter I from the vertices A, B, C, D are related to the inradius according to

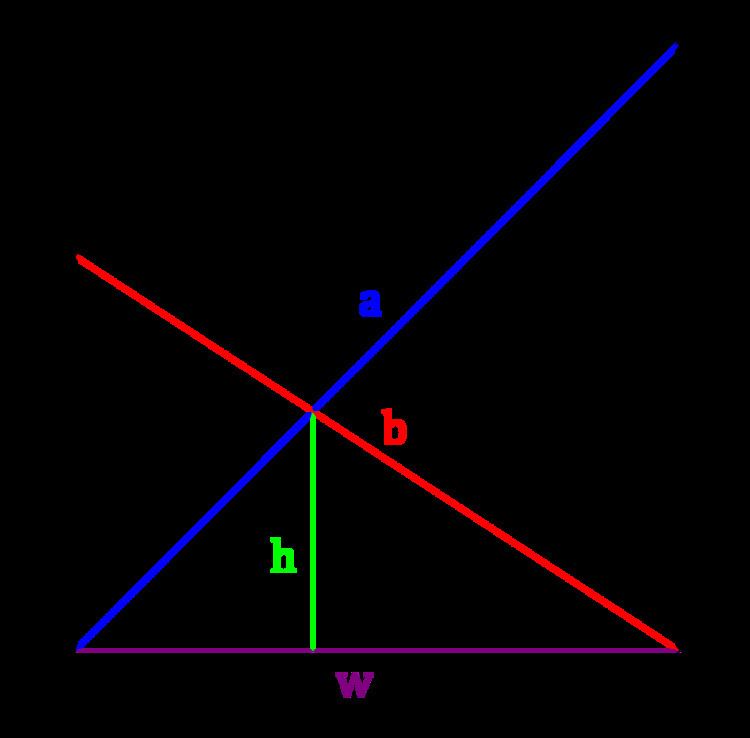
In the crossed ladders problem, two ladders braced at the bottoms of vertical walls cross at the height h and lean against the opposite walls at heights of A and B. We have 1 h = 1 A + 1 B . Moreover, the formula continues to hold if the walls are slanted and all three measurements are made parallel to the walls.

Let P be a point on the circumcircle of an equilateral triangle ABC, on the minor arc AB. Let a be the distance from P to A and b be the distance from P to B. On a line passing through P and the far vertex C, let c be the distance from P to the triangle side AB. Then 1 a + 1 b = 1 c .

In a trapezoid, draw a segment parallel to the two parallel sides, passing through the intersection of the diagonals and having endpoints on the non-parallel sides. Then if we denote the lengths of the parallel sides as a and b and half the length of the segment through the diagonal intersection as c, the sum of the reciprocals of a and b equals the reciprocal of c.

The special case in which the integers whose reciprocals are taken must be square numbers appears in two ways in the context of right triangles. First, the sum of the reciprocals of the squares of the altitudes from the legs (equivalently, of the squares of the legs themselves) equals the reciprocal of the square of the altitude from the hypotenuse. This holds whether or not the numbers are integers; there is a formula (see here) that generates all integer cases. Second, also in a right triangle the sum of the squared reciprocal of the side of one of the two inscribed squares and the squared reciprocal of the hypotenuse equals the squared reciprocal of the side of the other inscribed square.

The sides of a heptagonal triangle, which shares its vertices with a regular heptagon, satisfy the optic equation.

Thin lens equation

If the distances from an object to a lens and from a lens to the image are S1 and S2 respectively, for a lens of negligible thickness, in air, the distances are related by the thin lens formula:

Electrical engineering

Components of an electrical circuit or electronic circuit can be connected in what is called a series or parallel configuration. For example, the total resistance value r_t of two resistors with resistances r₁ and r₂ connected in parallel follows the optic equation:

Relation to Fermat's Last Theorem

Fermat's Last Theorem states that the sum of two integers each raised to the same integer power n cannot equal another integer raised to the power n if n > 2. This implies that no solutions to the optic equation have all three integers equal to perfect powers with the same power n > 2. For if 1 x n + 1 y n = 1 z n , then multiplying through by ( x y z ) n would give ( y z ) n + ( x z ) n = ( x y ) n , which is impossible by Fermat's Last Theorem.