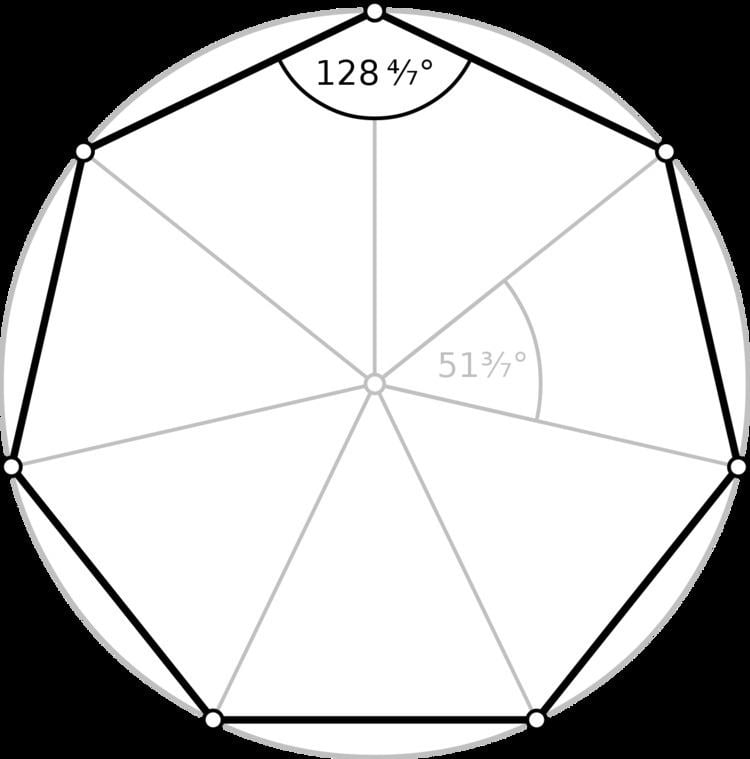
Schläfli symbol {7} Dual polygon Self | Edges and vertices 7 Internal angle (degrees) ≈128.571° | |
 | ||
Symmetry group Dihedral (D7), order 2×7 | ||
In geometry, a heptagon is a seven-sided polygon or 7-gon.
Contents
- Regular heptagon
- Area
- Construction
- Approximation
- Symmetry
- Diagonals and heptagonal triangle
- Star heptagons
- Uses
- Graphs
- References
The heptagon is also occasionally referred to as the septagon, using "sept-" (an elision of septua-, a Latin-derived numerical prefix, rather than hepta-, a Greek-derived numerical prefix) together with the Greek suffix "-agon" meaning angle.
Regular heptagon
A regular heptagon, in which all sides and all angles are equal, has internal angles of 5π/7 radians (128.5714286 degrees). Its Schläfli symbol is {7}.
Area
The area (A) of a regular heptagon of side length a is given by:
This can be seen by subdividing the unit-sided heptagon into seven triangular "pie slices" with vertices at the center and at the heptagon's vertices, and then halving each triangle using the apothem as the common side. The apothem is half the cotangent of
The exact algebraic expression, starting from the cubic polynomial x3 + x2 − 2x − 1 (one of whose roots is
in which the imaginary parts offset each other leaving a real-valued expression. This expression cannot be algebraically rewritten without complex components, since the indicated cubic function is casus irreducibilis.
The area of a regular heptagon inscribed in a circle of radius R is
Construction
As 7 is a Pierpont prime but not a Fermat prime, the regular heptagon is not constructible with compass and straightedge but is constructible with a marked ruler and compass. This type of construction is called a neusis construction. It is also constructible with compass, straightedge and angle trisector. The impossibility of straightedge and compass construction follows from the observation that
Approximation
An approximation for practical use with an error of about 0.2% is shown in the drawing. It is attributed to Albrecht Dürer. Let A lie on the circumference of the circumcircle. Draw arc BOC. Then
Example to illustrate the error:
At a circumscribed circle radius r = 1 m, the absolute error of the 1st side would be approximately -1.7 mm
Symmetry
The regular heptagon has Dih7 symmetry, order 14. Since 7 is a prime number there is one subgroup with dihedral symmetry: Dih1, and 2 cyclic group symmetries: Z7, and Z1.
These 4 symmetries can be seen in 4 distinct symmetries on the heptagon. John Conway labels these by a letter and group order. Full symmetry of the regular form is r14 and no symmetry is labeled a1. The dihedral symmetries are divided depending on whether they pass through vertices (d for diagonal) or edges (p for perpendiculars), and i when reflection lines path through both edges and vertices. Cyclic symmetries in the middle column are labeled as g for their central gyration orders.
Each subgroup symmetry allows one or more degrees of freedom for irregular forms. Only the g7 subgroup has no degrees of freedom but can seen as directed edges.
Diagonals and heptagonal triangle
The regular heptagon's side a, shorter diagonal b, and longer diagonal c, with a<b<c, satisfy
and hence
and
Thus –b/c, c/a, and a/b all satisfy the cubic equation
We also have
and
A heptagonal triangle has vertices coinciding with the first, second, and fourth vertices of a regular heptagon (from an arbtrary starting vertex) and angles
Star heptagons
Two kinds of star heptagons can be constructed from regular heptagons, labeled by Schläfli symbols {7/2}, and {7/3}, with the divisor being the interval of connection.
Blue, {7/2} and green {7/3} star heptagons inside a red heptagon.
Uses
The United Kingdom currently (2011) has two heptagonal coins, the 50p and 20p pieces, and the Barbados Dollar is also heptagonal. The 20-eurocent coin has cavities placed similarly. Strictly, the shape of the coins is a Reuleaux heptagon, a curvilinear heptagon to make them curves of constant width: the sides are curved outwards so that the coin will roll smoothly in vending machines. Botswana pula coins in the denominations of 2 Pula, 1 Pula, 50 Thebe and 5 Thebe are also shaped as equilateral-curve heptagons. Coins in the shape of Reuleaux heptagons are also in circulation in Mauritius, U.A.E., Tanzania, Samoa, Papua New Guinea, São Tomé and Príncipe, Haiti, Jamaica, Liberia, Ghana, the Gambia, Jordan, Jersey, Guernsey, Isle of Man, Gibraltar, Guyana, Solomon Islands, Falkland Islands and Saint Helena. The 1000 Kwacha coin of Zambia is a true heptagon.
The Brazilian 25-cent coin has a heptagon inscribed in the coin's disk. Some old versions of the coat of arms of Georgia, including in Soviet days, used a {7/2} heptagram as an element.
In architecture, heptagonal floor plans are very rare. A remarkable example is the Mausoleum of Prince Ernst in Stadthagen, Germany.
Many police badges in the US have a 7:2 heptagram outline.
Apart from the heptagonal prism and heptagonal antiprism, no convex polyhedron made entirely out of regular polygons contains a heptagon as a face.
Regular heptagons can tile the hyperbolic plane, as shown in this Poincaré disk model projection:
heptagonal tiling
Graphs
The K7 complete graph is often drawn as a regular heptagon with all 21 edges connected. This graph also represents an orthographic projection of the 7 vertices and 21 edges of the 6-simplex. The regular skew polygon around the perimeter is called the petrie polygon.
